归并排序的核心思路需要结合二叉树的后序遍历 来理解:先利用递归把左右两半子数组排好序,然后在二叉树的后序位置合并两个有序数组。
归并排序核心思路
前文快速排序的思路是,先把一个元素放到正确的位置(排好序),然后将这个元素左右两边剩下的元素利用递归分别排好序,最终整个数组就排好序了。代码框架如下:
def sort(nums: List[int], lo: int, hi: int):
if lo >= hi:
return
# ****** 前序位置 ******
# 对 nums[lo..hi] 进行切分,将 nums[p] 排好序
# 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
p = partition(nums, lo, hi)
# 去左右子数组进行切分
sort(nums, lo, p - 1)
sort(nums, p + 1, hi)
归并排序的思路是,把数组切成两半,先把这两半子数组分别排好序,然后再合并这两个有序数组,整个数组就排好序了。代码框架如下:
# 定义:排序 nums[lo..hi]
def sort(nums: List[int], lo: int, hi: int) -> None:
if lo == hi:
return
mid = (lo + hi) // 2
# 利用定义,排序 nums[lo..mid]
sort(nums, lo, mid)
# 利用定义,排序 nums[mid+1..hi]
sort(nums, mid + 1, hi)
# ****** 后序位置 ******
# 此时两部分子数组已经被排好序
# 合并两个有序数组,使 nums[lo..hi] 有序
merge(nums, lo, mid, hi)
时间复杂度
归并排序的时间复杂度是 $O(nlogn)$,其中 $n$ 是数组的长度。
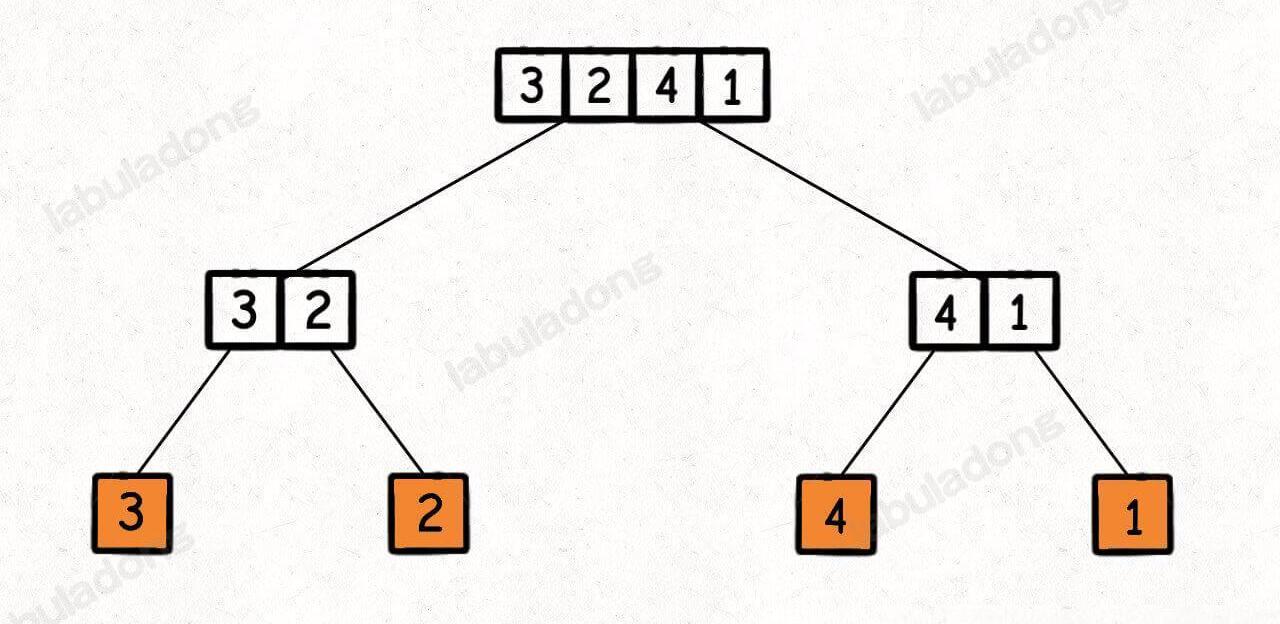
每向下一层,每个节点的数组元素就减半,但是每一层总的元素数量就是数组的长度 $O(n)$。
这棵二叉树是平衡二叉树,即树高是$O(logn)$,所以总的时间复杂度是 $O(nlogn)$,即树高乘以每层的复杂度。
空间复杂度
归并排序的空间复杂度是 $O(n)$,其中 $n$ 是数组的长度。
算法稳定性
归并排序是一种稳定的排序算法,归并排序的稳定性取决于 merge 函数的实现



