反转整个单链表
在 力扣/LeetCode 中,单链表的通用结构是这样的:
# 单链表节点的结构
class ListNode:
def __init__(self, x):
self.val = x
self.next = None单链表反转是一个比较基础的算法题,力扣第 206 题 反转链表 就是这个问题:
下面我们来尝试用多种方法解决这个问题。
迭代解法
这道题的常规做法就是迭代解法,通过操作几个指针,将链表中的每个节点的指针方向反转,没什么难点,主要是指针操作的细节问题。
这里直接给出代码:
class Solution:
# 反转以 head 为起点的单链表
def reverseList(self, head: ListNode) -> ListNode:
if head is None or head.next is None:
return head
# 由于单链表的结构,至少要用三个指针才能完成迭代反转
# cur 是当前遍历的节点,pre 是 cur 的前驱结点,nxt 是 cur 的后继结点
pre, cur, nxt = None, head, head.next
while cur is not None:
# 逐个结点反转
cur.next = pre
# 更新指针位置
pre = cur
cur = nxt
if nxt is not None:
nxt = nxt.next
# 返回反转后的头结点
return pre这个解法的思路是:
- 首先判断链表是否为空或只有一个结点,如果是,则直接返回原链表。
- 然后初始化三个指针:
pre是前驱指针,cur是当前指针,nxt是后继指针。 - 然后开始迭代,每次迭代都将当前结点的
next指针指向pre,然后更新pre、cur、nxt指针的位置。 - 最后返回
pre指针,即为反转后的头结点。
递归解法
上面的迭代解法操作指针虽然有些繁琐,但是思路还是比较清晰的。如果现在让你用递归来反转单链表,你有啥想法没?
递归反转单链表的关键在于,这个问题本身是存在子问题结构的。
比方说,现在给你输入一个以 1 为头结点单链表 1->2->3->4,那么如果我忽略这个头结点 1,只拿出 2->3->4 这个子链表,它也是个单链表对吧?
那么你这个 reverseList 函数,只要输入一个单链表,就能给我反转对吧?那么你能不能用这个函数先来反转 2->3->4 这个子链表呢,然后再想办法把 1 接到反转后的 4->3->2 的最后面,是不是就完成了整个链表的反转?
reverseList(1->2->3->4) = reverseList(2->3->4) -> 1这就是「分解问题」的思路,通过递归函数的定义,把原问题分解成若干规模更小、结构相同的子问题,最后通过子问题的答案组装原问题的解。
因此,我们可以用递归函数来反转单链表,如下:
class Solution:
# 定义:输入一个单链表头结点,将该链表反转,返回新的头结点
def reverseList(self, head):
if head is None or head.next is None:
return head
last = self.reverseList(head.next)
head.next.next = head
head.next = None
return last对于「分解问题」思路的递归算法,最重要的就是明确递归函数的定义。具体来说,我们的 reverseList 函数定义是这样的:
输入一个节点 head,将「以 head 为起点」的链表反转,并返回反转之后的头结点。
明白了函数的定义,再来看这个问题。比如说我们想反转这个链表:
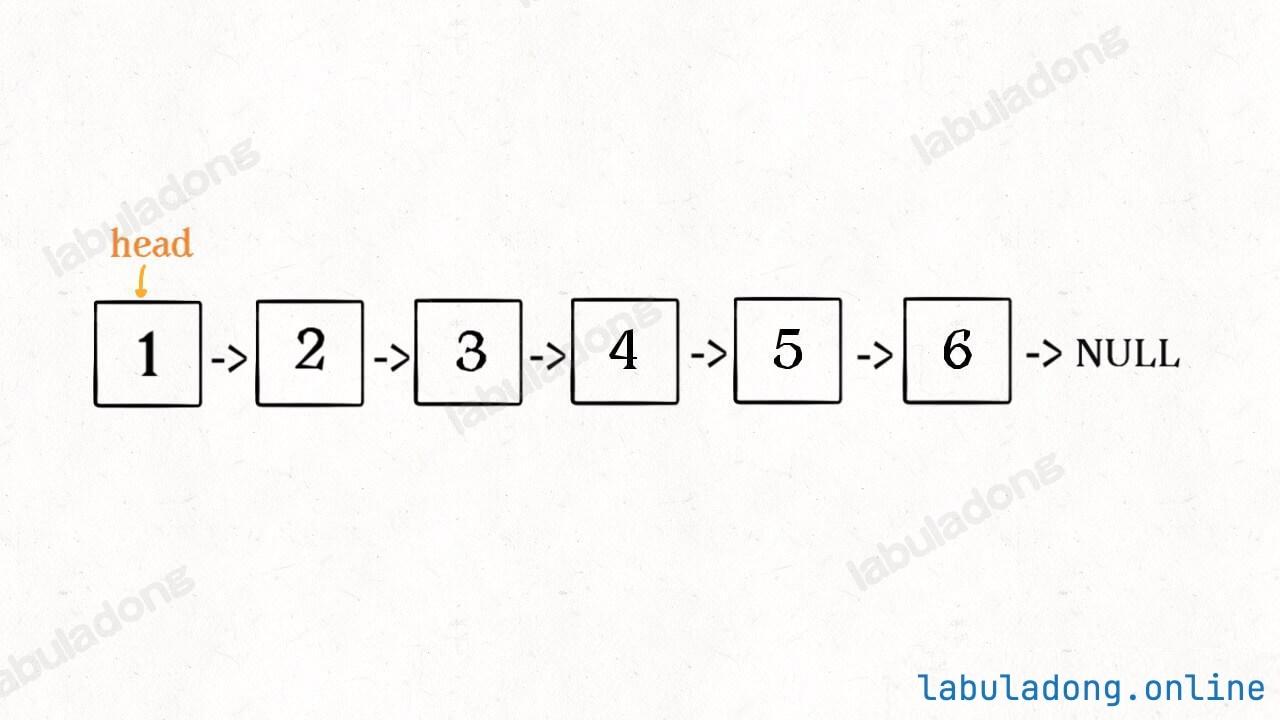
那么输入 reverseList(head) 后,会在这里进行递归:
ListNode last = reverseList(head.next);不要跳进递归(你的脑袋能压几个栈呀?),而是要根据刚才的函数定义,来弄清楚这段代码会产生什么结果:
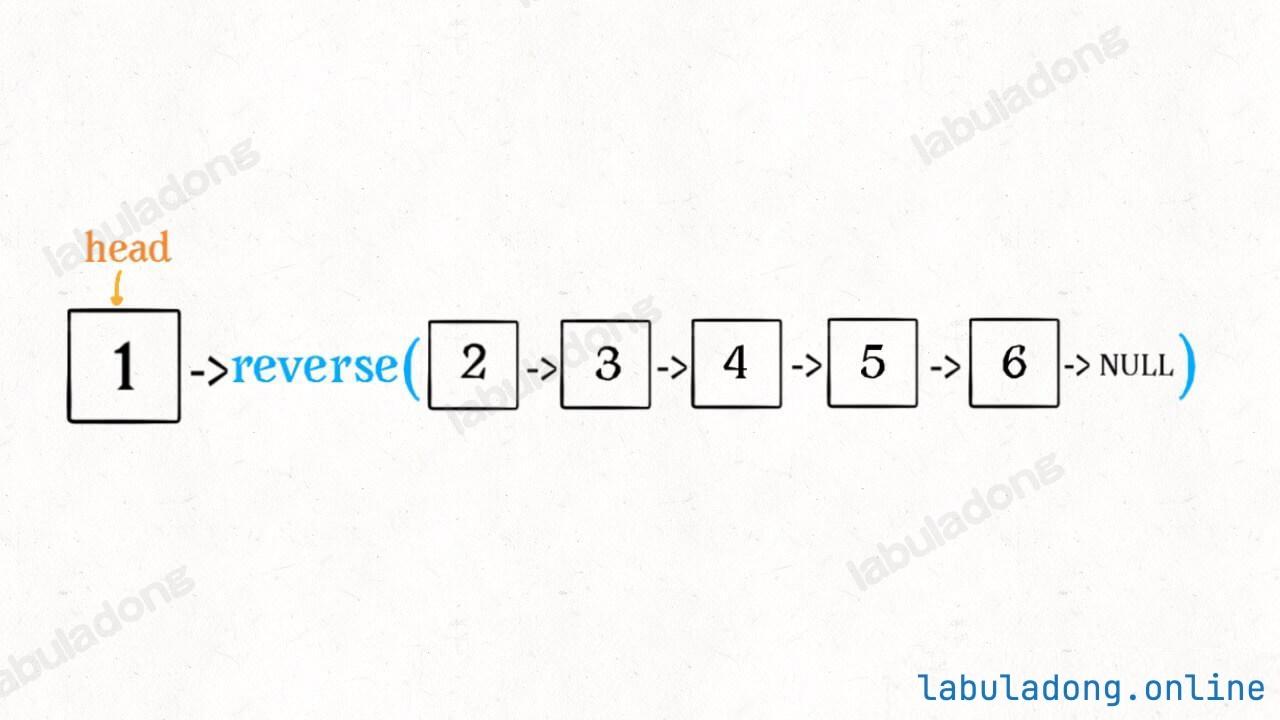
这个 reverseList(head.next) 执行完成后,整个链表就成了这样:
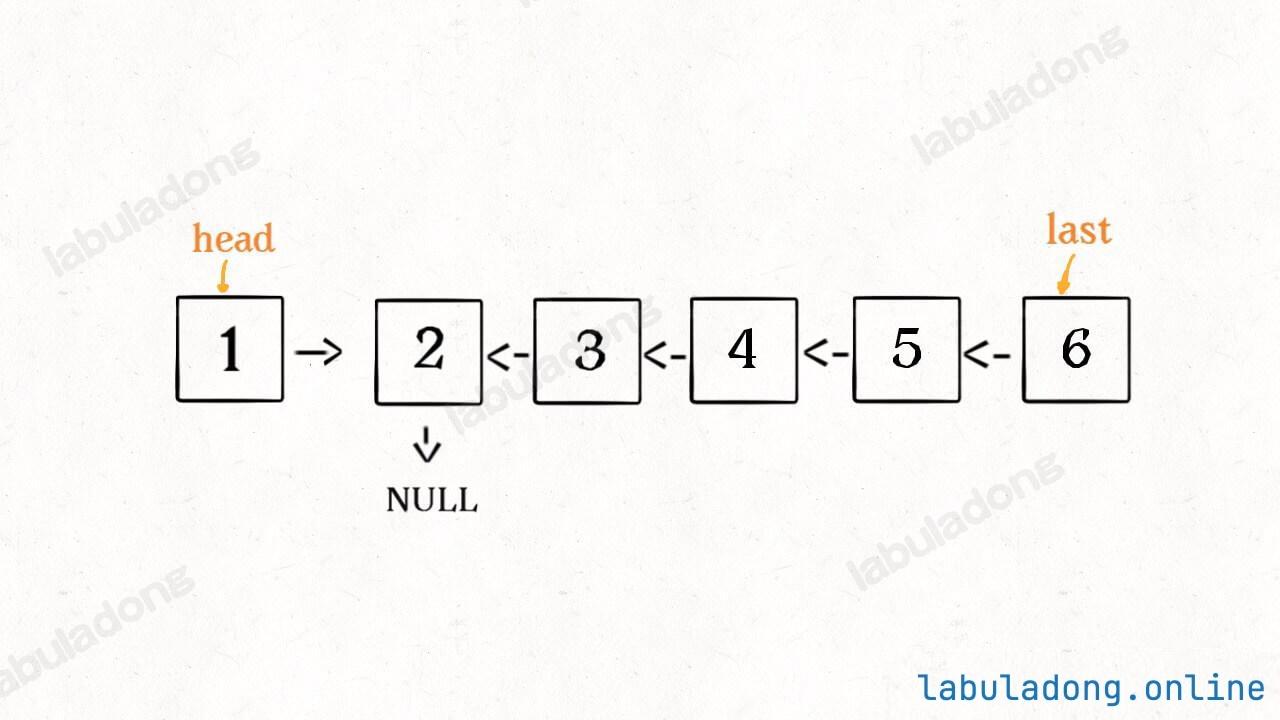
现在再来看下面的代码:
head.next.next = head;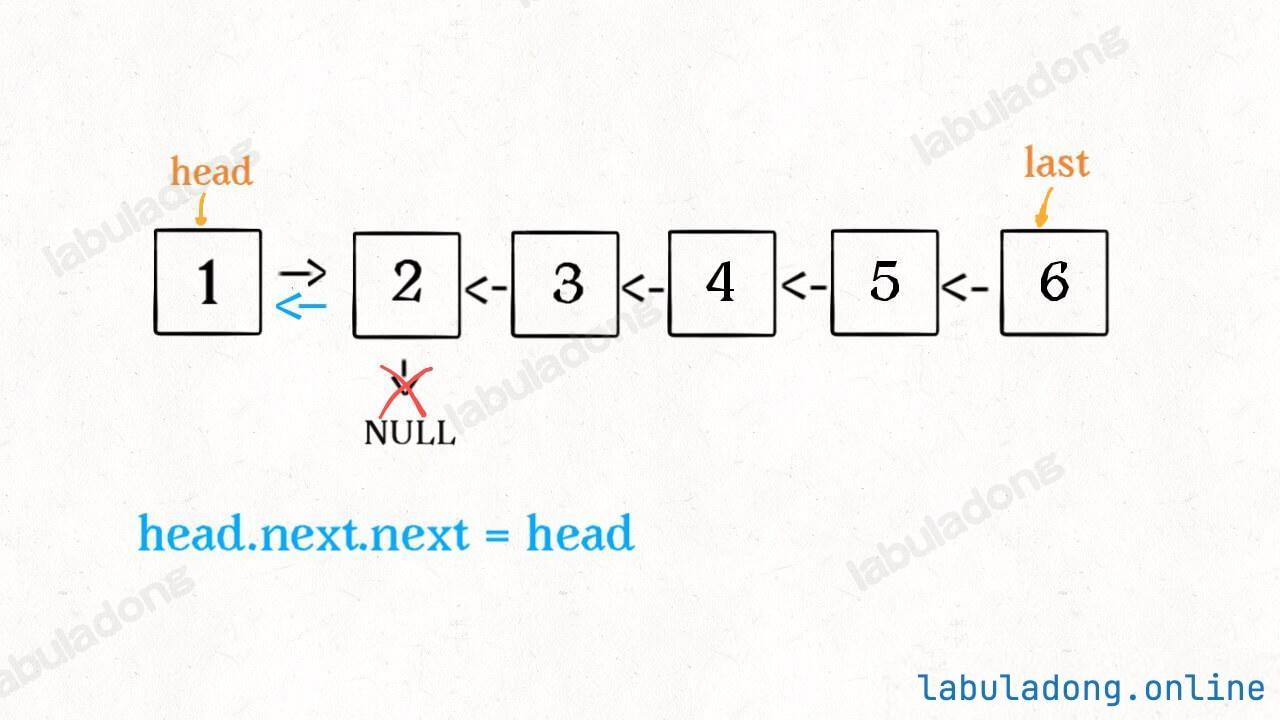
head.next = null;
return last;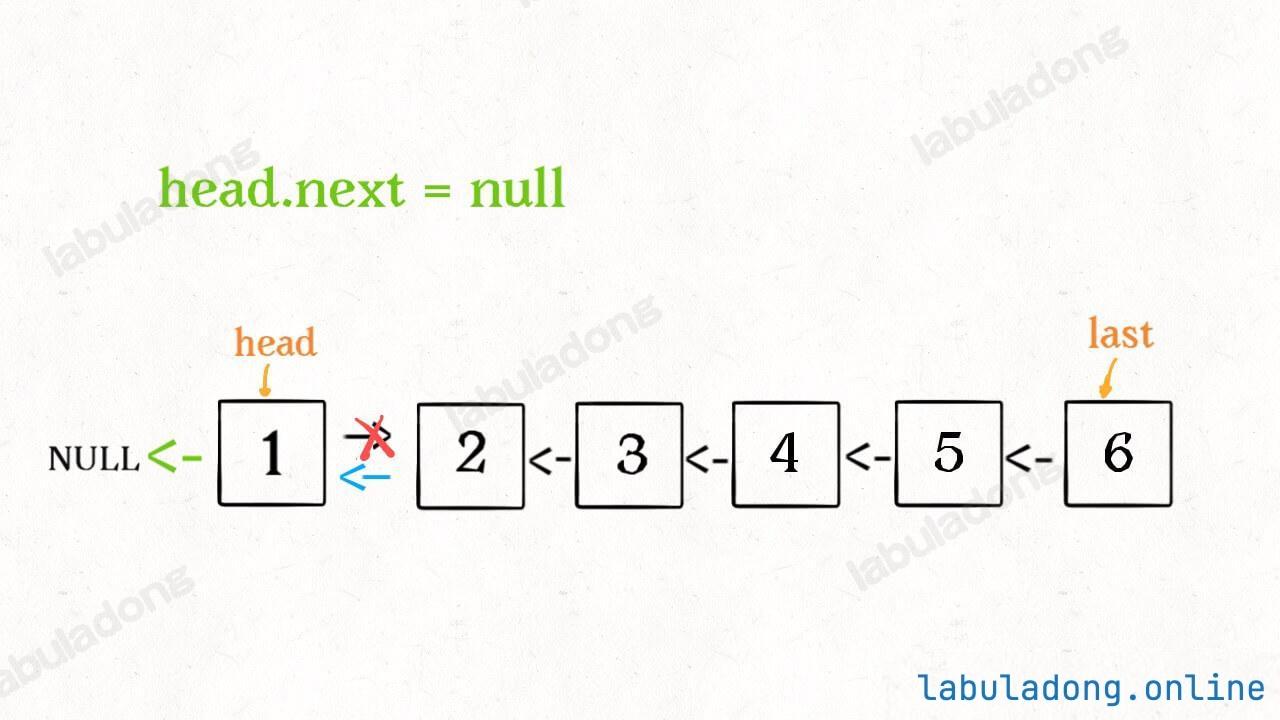
神不神奇,这样整个链表就反转过来了!递归代码就是这么简洁优雅,不过其中有两个地方需要注意:
1、递归函数要有 base case,也就是这句:
if (head == null || head.next == null) {
return head;
}意思是如果链表为空或者只有一个节点的时候,反转结果就是它自己,直接返回即可。
2、当链表递归反转之后,新的头结点是 last,而之前的 head 变成了最后一个节点,别忘了链表的末尾要指向 null:
head.next = null;这样,整个单链表就完成反转了。
递归操作链表的效率不如迭代
值得一提的是,递归操作链表并不高效。
递归解法和迭代解法相比,时间复杂度都是 O(N),但是迭代解法的空间复杂度是 O(1),而递归解法需要堆栈,空间复杂度是 O(N)。
所以递归操作链表可以用来练习递归思维,但是考虑效率的话还是使用迭代算法更好。
反转链表前 N 个节点
这次我们实现一个这样的函数:
# 将链表的前 n 个节点反转(n <= 链表长度)
def reverseN(head: ListNode, n: int):比如说对于下图链表,执行 reverseN(head, 3):
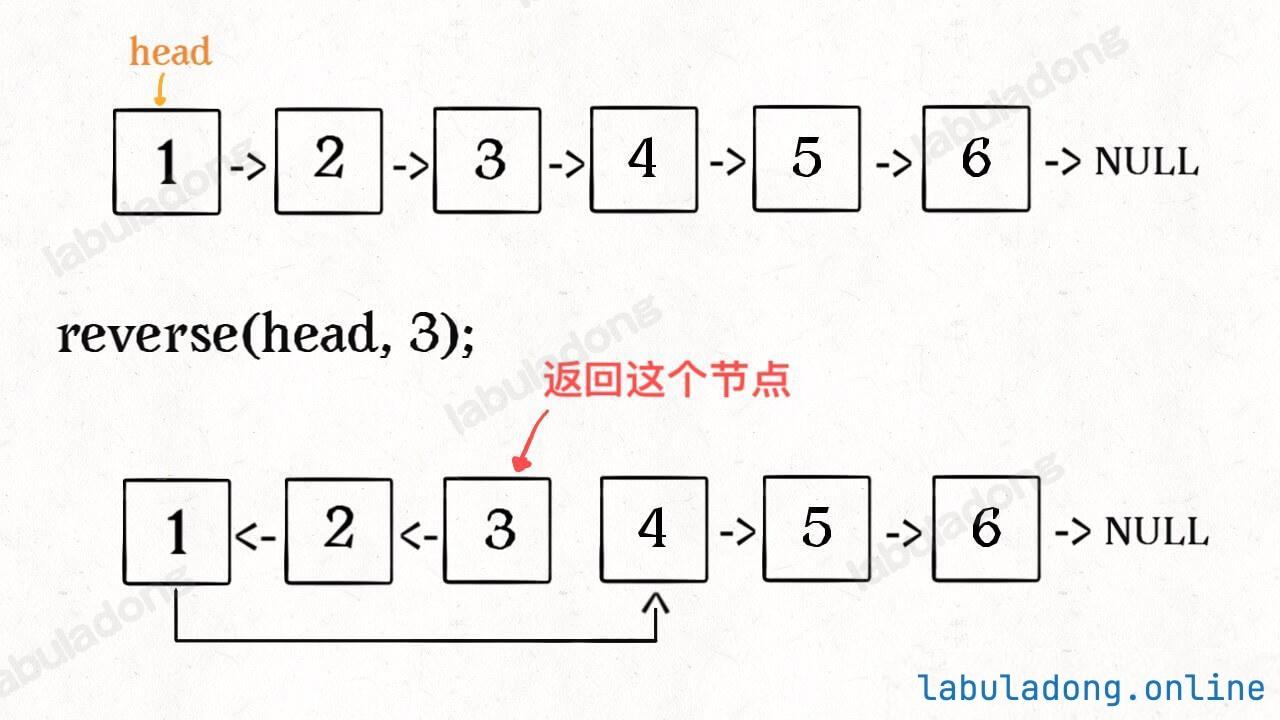
迭代解法
迭代解法应该比较好写,在之前实现的 reverseList 基础上稍加修改就可以了:
def reverseN(head: ListNode, n: int):
if head is None or head.next is None:
return head
pre, cur, nxt = None, head, head.next
while n > 0:
cur.next = pre
pre = cur
cur = nxt
if nxt is not None:
nxt = nxt.next
n -= 1
# 此时的 cur 是第 n + 1 个节点,head 是反转后的尾结点
head.next = cur
# 此时的 pre 是反转后的头结点
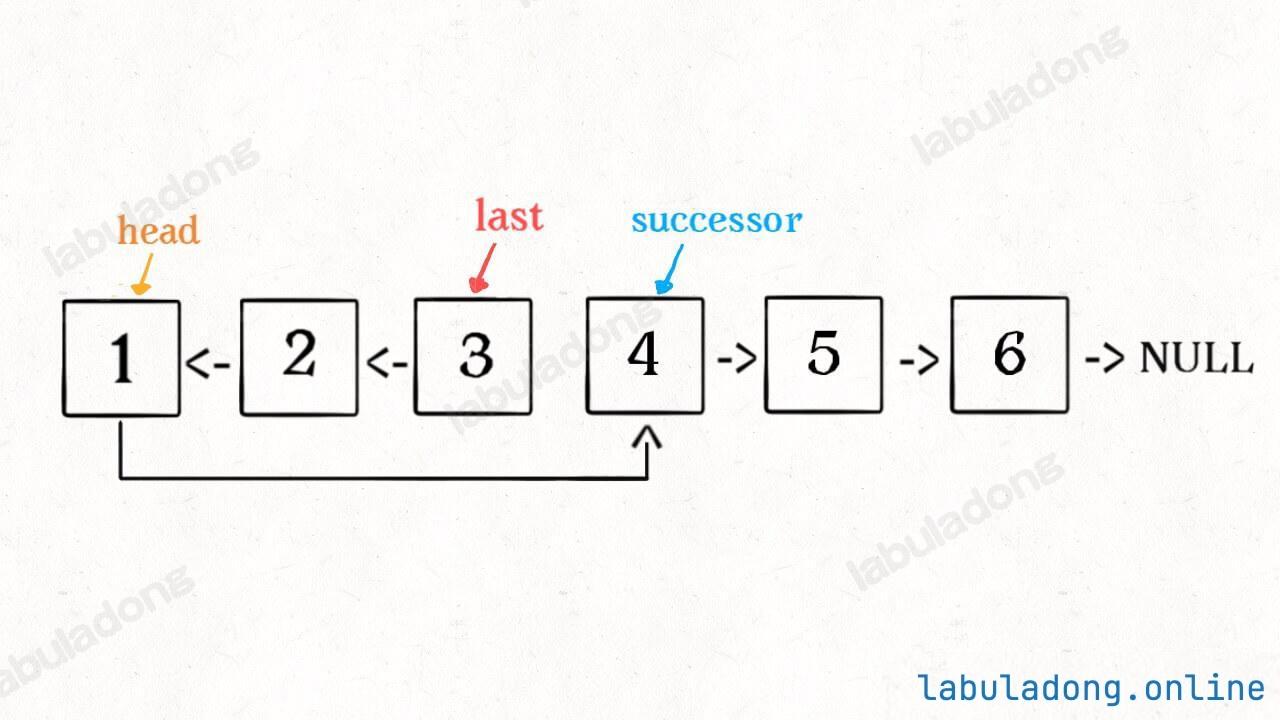
return pre递归解法
# 后驱节点
successor = None
# 反转以 head 为起点的 n 个节点,返回新的头结点
def reverseN(head: ListNode, n: int):
global successor
if n == 1:
# 记录第 n + 1 个节点
successor = head.next
return head
# 以 head.next 为起点,需要反转前 n - 1 个节点
last = reverseN(head.next, n - 1)
head.next.next = head
# 让反转之后的 head 节点和后面的节点连起来
head.next = successor
return last 具体的区别:
1、base case 变为 n == 1,反转一个元素,就是它本身,同时要记录后驱节点,即要记录第 n + 1 个节点。
2、刚才我们直接把 head.next 设置为 null,因为整个链表反转后原来的 head 变成了整个链表的最后一个节点。但现在 head 节点在递归反转之后不一定是最后一个节点了,所以要记录后驱 successor(第 n + 1 个节点),反转之后将 head 连接上。