单调队列结构解决滑动窗口问题

前文用单调栈解决三道算法问题介绍了单调栈这种特殊数据结构，本文写一个类似的数据结构「单调队列」。

也许这种数据结构的名字你没听过，其实没啥难的，就是一个「队列」，只是使用了一点巧妙的方法，使得队列中的元素全都是单调递增（或递减）的。

为啥要发明「单调队列」这种结构呢，主要是为了解决下面这个场景：

给你一个数组 window，已知其最值为 A，如果给 window 中添加一个数 B，那么比较一下 A 和 B 就可以立即算出新的最值；但如果要从 window 数组中减少一个数，就不能直接得到最值了，因为如果减少的这个数恰好是 A，就需要遍历 window 中的所有元素重新寻找新的最值。

这个场景很常见，但不用单调队列似乎也可以，比如优先级队列（二叉堆）就是专门用来动态寻找最值的，我创建一个大（小）顶堆，不就可以很快拿到最大（小）值了吗？

如果单纯地维护最值的话，优先级队列很专业，队头元素就是最值。但优先级队列无法满足标准队列结构「先进先出」的时间顺序，因为优先级队列底层利用二叉堆对元素进行动态排序，元素的出队顺序是元素的大小顺序，和入队的先后顺序完全没有关系。

所以，现在需要一种新的队列结构，既能够维护队列元素「先进先出」的时间顺序，又能够正确维护队列中所有元素的最值，这就是「单调队列」结构。

「单调队列」这个数据结构主要用来辅助解决滑动窗口相关的问题，前文滑动窗口核心框架把滑动窗口算法作为双指针技巧的一部分进行了讲解，但有些稍微复杂的滑动窗口问题不能只靠两个指针来解决，需要上更先进的数据结构。

比方说，你注意看前文滑动窗口核心框架讲的几道题目，每当窗口扩大（right++）和窗口缩小（left++）时，你单凭移出和移入窗口的元素即可决定是否更新答案。

但本文开头说的那个判断一个窗口中最值的例子，你无法单凭移出窗口的那个元素更新窗口的最值，除非重新遍历所有元素，但这样的话时间复杂度就上来了，这是我们不希望看到的。

我们来看看力扣第 239 题「滑动窗口最大值」，就是一道标准的滑动窗口问题：

给你输入一个数组 nums 和一个正整数 k，有一个大小为 k 的窗口在 nums 上从左至右滑动，请你输出每次窗口中 k 个元素的最大值。

函数签名如下：

def maxSlidingWindow(nums: List[int], k: int) -> List[int]:

比如说力扣给出的一个示例：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

接下来，我们就借助单调队列结构，用 O(1)O(1) 时间算出每个滑动窗口中的最大值，使得整个算法在线性时间完成。

一、搭建解题框架

在介绍「单调队列」这种数据结构的 API 之前，先来对比一下普通的队列的标准 API 和单调队列实现的 API：

# 普通队列的 API
class Queue:
    # enqueue 操作，在队尾加入元素 n
    def push(self, n: int):
        pass
    
    # dequeue 操作，删除队头元素
    def pop(self):
        pass

# 单调队列的 API
class MonotonicQueue:
    # 在队尾添加元素 n
    def push(self, n: int):
        pass

    # 返回当前队列中的最大值
    def max(self) -> int:
        pass

    # 队头元素如果是 n，删除它
    def pop(self, n: int):
        pass

当然，单调队列这几个 API 的实现方法肯定跟一般的 Queue 不一样，不过我们暂且不管，而且认为这几个操作的时间复杂度都是 O(1)，先把这道「滑动窗口」问题的解答框架搭出来：

from collections import deque
from typing import List

def maxSlidingWindow(nums: List[int], k: int) -> List[int]:
    window = MonotonicQueue()
    res = []

    for i in range(len(nums)):
        if i < k - 1:
            # 先将窗口前 k - 1 填满
            window.append(nums[i])
        else:
            # 窗口开始向前滑动
            # 移入新元素
            window.append(nums[i])
            # 将当前窗口中的最大元素记入结果
            res.append(max(window))
            # 移出最后的元素
            window.popleft()

    # 将 List 类型转化成 int[] 数组作为返回值
    return res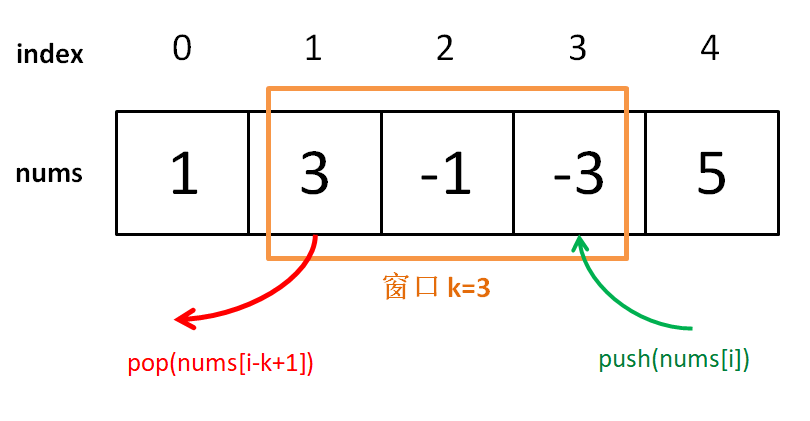

这个思路很简单吧，下面我们开始重头戏，单调队列的实现。

二、实现单调队列数据结构

观察滑动窗口的过程就能发现，实现「单调队列」必须使用一种数据结构支持在头部和尾部进行插入和删除，很明显双链表是满足这个条件的。

「单调队列」的核心思路和「单调栈」类似，push 方法依然在队尾添加元素，但是要把前面比自己小的元素都删掉：

from collections import deque

class MonotonicQueue:
    
    def __init__(self):
        # 使用双端队列，支持头部和尾部增删元素
        # 维护其中的元素自尾部到头部单调递增
        self.maxq = deque()
    
    # 在尾部添加一个元素 n，维护 maxq 的单调性质
    def push(self, n: int) -> None:
        # 将前面小于自己的元素都删除
        while len(self.maxq) > 0 and self.maxq[-1] < n:
            self.maxq.pop()
        self.maxq.append(n)

你可以想象，加入数字的大小代表人的体重，体重大的会把前面体重不足的压扁，直到遇到更大的量级才停住。

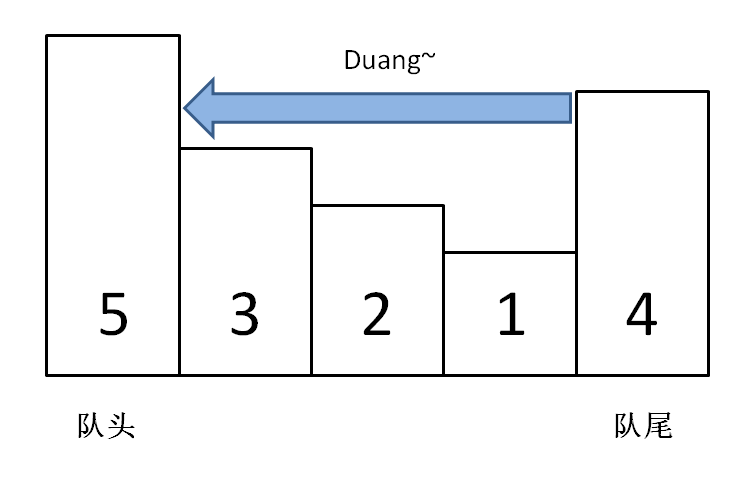
如果每个元素被加入时都这样操作，最终单调队列中的元素大小就会保持一个单调递减的顺序，因此我们的 max 方法就很好写了，只要把队头元素返回即可；pop 方法也是操作队头，如果队头元素是待删除元素 n，那么就删除它：

class MonotonicQueue:
    # 为了节约篇幅，省略上文给出的代码部分...

    def max(self) -> int:
        # 队头的元素肯定是最大的
        return self.maxq[0]

    def pop(self, n: int) -> None:
        if n == self.maxq[0]:
            self.maxq.popleft()

pop 方法之所以要判断 n == maxq.getFirst()，是因为我们想删除的队头元素 n 可能已经在 push 的过程中被「压扁」了，可能已经不存在了，这种情况就不用删除了：

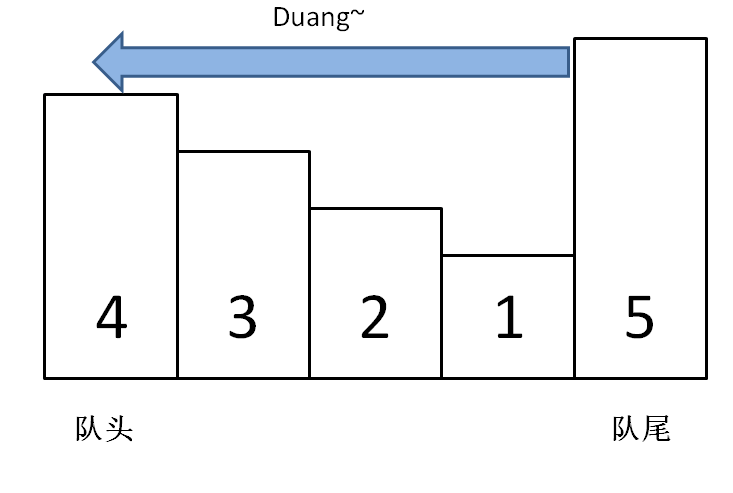
至此，单调队列设计完毕，看下完整的解题代码：

class MonotonicQueue:
    def __init__(self):
        self.maxq = []
    
    def push(self, n):
        # 将小于 n 的元素全部删除
        while self.maxq and self.maxq[-1] < n: 
            self.maxq.pop()
        # 然后将 n 加入尾部
        self.maxq.append(n)
    
    def max(self):
        return self.maxq[0]
    
    def pop(self, n):
        if n == self.maxq[0]:
            self.maxq.pop(0)

class Solution(object):
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        window = MonotonicQueue()
        res = []
        
        for i in range(len(nums)):
            if i < k - 1:
                # 先填满窗口的前 k - 1
                window.push(nums[i])
            else: 
                # 窗口向前滑动，加入新数字
                window.push(nums[i])
                # 记录当前窗口的最大值
                res.append(window.max())
                # 移出旧数字
                window.pop(nums[i - k + 1])
        return res

有一点细节问题不要忽略，在实现 MonotonicQueue 时，我们使用了 Java 的 LinkedList，因为链表结构支持在头部和尾部快速增删元素；而在解法代码中的 res 则使用的 ArrayList 结构，因为后续会按照索引取元素，所以数组结构更合适。其他语言的实现也要注意这些细节。

关于单调队列 API 的时间复杂度，读者可能有疑惑：push 操作中含有 while 循环，最坏情况下的时间复杂度应该 O(N)O(N) 呀，再加上一层 for 循环，本算法的时间复杂度应该是 O(N2)O(N2) 才对吧？

这里就用到了算法时空复杂度分析指南中讲到的摊还分析：

单独看 push 操作，最坏时间复杂度确实是 O(N)O(N)，但是平均时间复杂度是 O(1)O(1)。我们一般用平均复杂度而不是最坏时间复杂度来衡量 API 接口，所以这个算法整体的时间复杂度是 O(N)O(N)，而不是 O(N2)O(N2)。

也可以这样从整体上分析：整个算法做的事情就是把 nums 中的每个元素加入和移出 window 至多一次，不可能把同一个元素多次移入移出 window，所以整体的时间复杂度是 O(N)O(N)。

空间复杂度很容易分析，就是窗口的大小 O(k)O(k)。

拓展延伸

最后，我提出几个问题请大家思考：

1、本文给出的 MonotonicQueue 类只实现了 max 方法，你是否能够再额外添加一个 min 方法，在 O(1)O(1) 的时间返回队列中所有元素的最小值？

2、本文给出的 MonotonicQueue 类的 pop 方法还需要接收一个参数，这不那么优雅，而且有悖于标准队列的 API，请你修复这个缺陷。

3、请你实现 MonotonicQueue 类的 size 方法，返回单调队列中元素的个数（注意，由于每次 push 方法都可能从底层的 q 列表中删除元素，所以 q 中的元素个数并不是单调队列的元素个数）。

也就是说，你是否能够实现单调队列的通用实现：

# 单调队列的通用实现，可以高效维护最大值和最小值
class MonotonicQueue:
    def push(self, elem: 'Comparable') -> None:
        pass
    
    # 标准队列 API，从队头弹出元素，符合先进先出的顺序
    def pop(self) -> 'Comparable':
        pass
    
    # 标准队列 API，返回队列中的元素个数
    def size(self) -> int:
        pass
    
    # 单调队列特有 API，O(1) 时间计算队列中元素的最大值
    def max(self) -> 'Comparable':
        pass
    
    # 单调队列特有 API，O(1) 时间计算队列中元素的最小值
    def min(self) -> 'Comparable':
        pass