单调栈算法模板解决三道例题

栈（stack）是很简单的一种数据结构，先进后出的逻辑顺序，符合某些问题的特点，比如说函数调用栈。单调栈实际上就是栈，只是利用了一些巧妙的逻辑，使得每次新元素入栈后，栈内的元素都保持有序（单调递增或单调递减）。

听起来有点像堆（heap）？不是的，单调栈用途不太广泛，只处理一类典型的问题，比如「下一个更大元素」，「上一个更小元素」等。本文讲解单调栈的算法模版解决「下一个更大元素」相关问题，并且探讨处理「循环数组」的策略。

单调栈模板

现在给你出这么一道题：输入一个数组 nums，请你返回一个等长的结果数组，结果数组中对应索引存储着下一个更大元素，如果没有更大的元素，就存 -1。函数签名如下：

def calculateGreaterElement(nums: List[int])

比如说，输入一个数组 nums = [2,1,2,4,3]，你返回数组 [4,2,4,-1,-1]。因为第一个 2 后面比 2 大的数是 4; 1 后面比 1 大的数是 2；第二个 2 后面比 2 大的数是 4; 4 后面没有比 4 大的数，填 -1；3 后面没有比 3 大的数，填 -1。

这道题的暴力解法很好想到，就是对每个元素后面都进行扫描，找到第一个更大的元素就行了。但是暴力解法的时间复杂度是 O(n2)O(n2)。

这个问题可以这样抽象思考：把数组的元素想象成并列站立的人，元素大小想象成人的身高。这些人面对你站成一列，如何求元素「2」的下一个更大元素呢？很简单，如果能够看到元素「2」，那么他后面可见的第一个人就是「2」的下一个更大元素，因为比「2」小的元素身高不够，都被「2」挡住了，第一个露出来的就是答案。

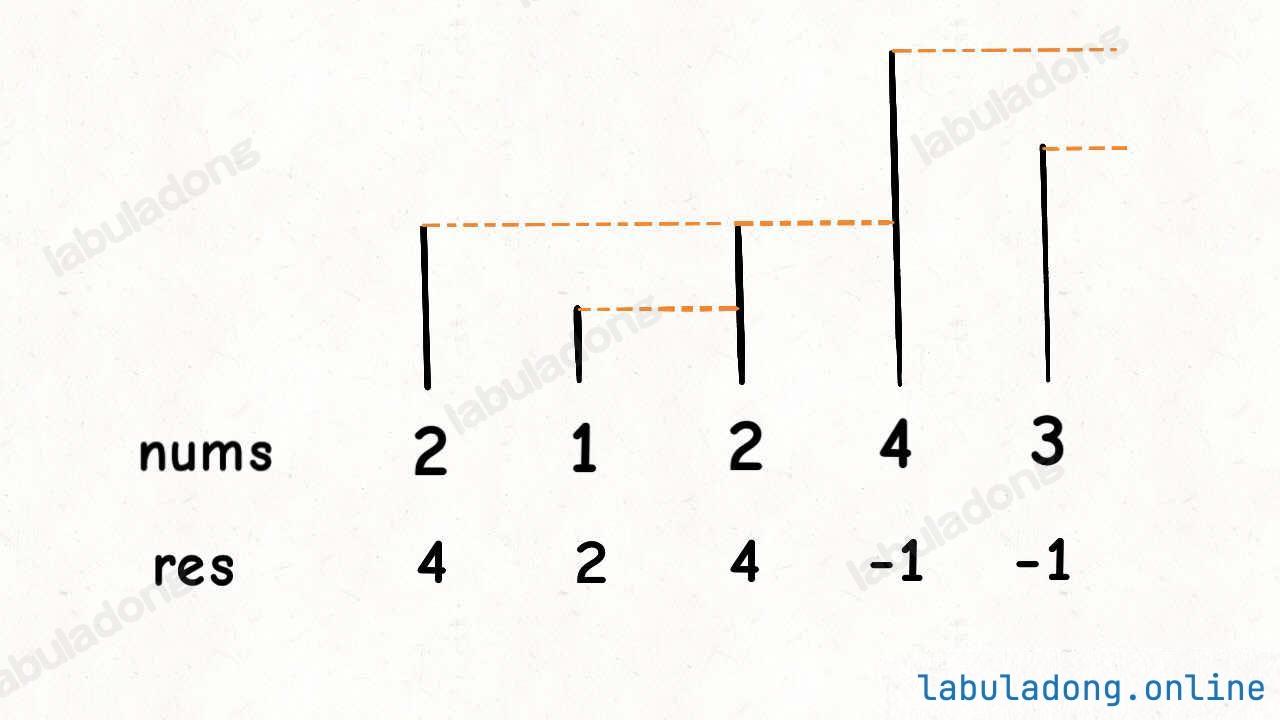
这个情景很好理解吧？带着这个抽象的情景，先来看下代码。

def calculateGreaterElement(nums):
    n = len(nums)
    # 存放答案的数组
    res = [0]*n
    s = []
    # 倒着往栈里放
    for i in range(n-1, -1, -1):
        # 判定个子高矮
        while s and s[-1] <= nums[i]:
            # 矮个起开，反正也被挡着了。。。
            s.pop()
        # nums[i] 身后的更大元素
        res[i] = -1 if not s else s[-1]
        s.append(nums[i])
    return res

这就是单调栈解决问题的模板。for 循环要从后往前扫描元素，因为我们借助的是栈的结构，倒着入栈，其实是正着出栈。while 循环是把两个「个子高」元素之间的元素排除，因为他们的存在没有意义，前面挡着个「更高」的元素，所以他们不可能被作为后续进来的元素的下一个更大元素了。

这个算法的时间复杂度不是那么直观，如果你看到 for 循环嵌套 while 循环，可能认为这个算法的复杂度也是 O(n2)O(n2)，但是实际上这个算法的复杂度只有 O(n)O(n)。

分析它的时间复杂度，要从整体来看：总共有 n 个元素，每个元素都被 push 入栈了一次，而最多会被 pop 一次，没有任何冗余操作。所以总的计算规模是和元素规模 n 成正比的，也就是 O(n)O(n) 的复杂度。

问题变形

单调栈的代码实现比较简单，下面来看一些具体题目。

496. 下一个更大元素 I

首先来一个简单的变形，力扣第 496 题「下一个更大元素 I」：

496. 下一个更大元素 I | 力扣 | LeetCode |  🟢

nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。

给你两个 没有重复元素 的数组 nums1 和 nums2 ，下标从 0 开始计数，其中nums1 是 nums2 的子集。

对于每个 0 <= i < nums1.length ，找出满足 nums1[i] == nums2[j] 的下标 j ，并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素，那么本次查询的答案是 -1 。

返回一个长度为 nums1.length 的数组 ans 作为答案，满足 ans[i] 是如上所述的 下一个更大元素 。

示例 1：

输入：nums1 = [4,1,2], nums2 = [1,3,4,2].
输出：[-1,3,-1]
解释：nums1 中每个值的下一个更大元素如下所述：
- 4 ，用加粗斜体标识，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。
- 1 ，用加粗斜体标识，nums2 = [1,3,4,2]。下一个更大元素是 3 。
- 2 ，用加粗斜体标识，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。

示例 2：

输入：nums1 = [2,4], nums2 = [1,2,3,4].
输出：[3,-1]
解释：nums1 中每个值的下一个更大元素如下所述：
- 2 ，用加粗斜体标识，nums2 = [1,2,3,4]。下一个更大元素是 3 。
- 4 ，用加粗斜体标识，nums2 = [1,2,3,4]。不存在下一个更大元素，所以答案是 -1 。

提示：

• 1 <= nums1.length <= nums2.length <= 1000
• 0 <= nums1[i], nums2[i] <= 104
• nums1和nums2中所有整数 互不相同
• nums1 中的所有整数同样出现在 nums2 中

进阶：你可以设计一个时间复杂度为 O(nums1.length + nums2.length) 的解决方案吗？

题目来源：力扣 496. 下一个更大元素 I。

这道题给你输入两个数组 nums1 和 nums2，让你求 nums1 中的元素在 nums2 中的下一个更大元素，函数签名如下：

from typing import List

def nextGreaterElement(nums1: List[int], nums2: List[int]) -> List[int]:

其实和把我们刚才的代码改一改就可以解决这道题了，因为题目说 nums1 是 nums2 的子集，那么我们先把 nums2 中每个元素的下一个更大元素算出来存到一个映射里，然后再让 nums1 中的元素去查表即可：

class Solution:
    def nextGreaterElement(self, nums1, nums2):
        # 记录 nums2 中每个元素的下一个更大元素
        greater = self.calculateGreaterElement(nums2)
        # 转化成映射：元素 x -> x 的下一个最大元素
        greaterMap = {}
        for i in range(len(nums2)):
            greaterMap[nums2[i]] = greater[i]
        # nums1 是 nums2 的子集，所以根据 greaterMap 可以得到结果
        res = [0] * len(nums1)
        for i in range(len(nums1)):
            res[i] = greaterMap[nums1[i]]
        return res

    def calculateGreaterElement(self, nums):
        # 见上文
        pass

 算法可视化面板

739. 每日温度

再看看力扣第 739 题「每日温度」：

给你一个数组 temperatures，这个数组存放的是近几天的天气气温，你返回一个等长的数组，计算：对于每一天，你还要至少等多少天才能等到一个更暖和的气温；如果等不到那一天，填 0。函数签名如下：

def dailyTemperatures(temperatures: List[int]) -> List[int]:

比如说给你输入 temperatures = [73,74,75,71,69,76]，你返回 [1,1,3,2,1,0]。因为第一天 73 华氏度，第二天 74 华氏度，比 73 大，所以对于第一天，只要等一天就能等到一个更暖和的气温，后面的同理。

这个问题本质上也是找下一个更大元素，只不过现在不是问你下一个更大元素的值是多少，而是问你当前元素距离下一个更大元素的索引距离而已。

相同的思路，直接调用单调栈的算法模板，稍作改动就可以，直接上代码吧：

class Solution:
    def dailyTemperatures(self, temperatures):
        n = len(temperatures)
        res = [0]*n
        # 这里放元素索引，而不是元素
        s = []
        # 单调栈模板
        for i in range(n-1, -1, -1):
            while s and temperatures[s[-1]] <= temperatures[i]:
                s.pop()
            # 得到索引间距
            res[i] = 0 if not s else s[-1] - i
            # 将索引入栈，而不是元素
            s.append(i)
        return res

单调栈讲解完毕，下面开始另一个重点：如何处理「循环数组」。

如何处理环形数组

同样是求下一个更大元素，现在假设给你的数组是个环形的，如何处理？力扣第 503 题「下一个更大元素 II」就是这个问题：输入一个「环形数组」，请你计算其中每个元素的下一个更大元素。

比如输入 [2,1,2,4,3]，你应该返回 [4,2,4,-1,4]，因为拥有了环形属性，最后一个元素 3 绕了一圈后找到了比自己大的元素 4。

如果你看过基础知识章节的 环形数组技巧 应该比较熟悉，我们一般是通过 % 运算符求模（余数），来模拟环形特效：

arr = [1,2,3,4,5]
n = len(arr)
index = 0
while True:
    # 在环形数组中转圈
    print(arr[index % n])
    index += 1

这个问题肯定还是要用单调栈的解题模板，但难点在于，比如输入是 [2,1,2,4,3]，对于最后一个元素 3，如何找到元素 4 作为下一个更大元素。

对于这种需求，常用套路就是将数组长度翻倍：

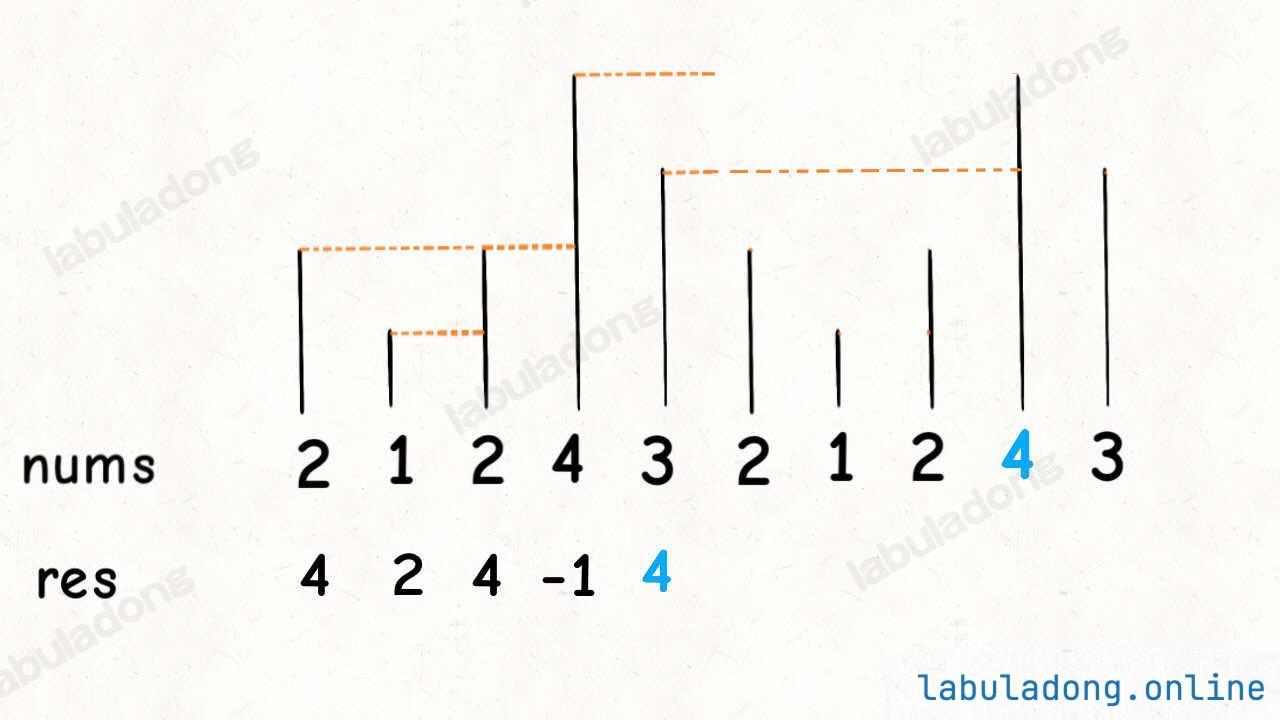
这样，元素 3 就可以找到元素 4 作为下一个更大元素了，而且其他的元素都可以被正确地计算。

有了思路，最简单的实现方式当然可以把这个双倍长度的数组构造出来，然后套用算法模板。但是，我们可以不用构造新数组，而是利用循环数组的技巧来模拟数组长度翻倍的效果。直接看代码吧：

class Solution:
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        n = len(nums)
        res = [0] * n
        # 用数组模拟栈
        s = []
        # 数组长度加倍模拟环形数组
        for i in range(2 * n - 1, -1, -1):
            # 索引 i 要求模，其他的和模板一样
            while s and s[-1] <= nums[i % n]:
                s.pop()
            res[i % n] = -1 if not s else s[-1]
            s.append(nums[i % n])
        return res

 算法可视化面板

这样，就可以巧妙解决环形数组的问题，时间复杂度 O(N)O(N)。

最后提出一些问题吧，本文提供的单调栈模板是 nextGreaterElement 函数，可以计算每个元素的下一个更大元素，但如果题目让你计算上一个更大元素，或者计算上一个更大或相等的元素，应该如何修改对应的模板呢？而且在实际应用中，题目不会直接让你计算下一个（上一个）更大（小）的元素，你如何把问题转化成单调栈相关的问题呢？

我会在 单调栈的几种变体及习题 对比单调栈的几种其他形式，并在 给出单调栈的经典例题。更多数据结构设计类题目参见 数据结构设计经典习题。