【练习】括号类问题汇总

20. 有效的括号

对括号的有效性判断多次在笔试中出现，现实中也很常见，比如说我们写的代码，编辑器会检查括号是否正确闭合。而且我们的代码可能会包含三种括号 [](){}，判断起来有一点难度。

来看一看力扣第 20 题「有效的括号」，输入一个字符串，其中包含 [](){} 六种括号，请你判断这个字符串组成的括号是否有效：

20. 有效的括号 | 力扣 | LeetCode |  🟢

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。
3. 每个右括号都有一个对应的相同类型的左括号。

示例 1：

输入：s = "()"
输出：true

示例 2：

输入：s = "()[]{}"
输出：true

示例 3：

输入：s = "(]"
输出：false

提示：

• 1 <= s.length <= 104
• s 仅由括号 '()[]{}' 组成

题目来源：力扣 20. 有效的括号。

解决这个问题之前，我们先降低难度，思考一下，如果只有一种括号 ()，应该如何判断字符串组成的括号是否有效呢？

假设字符串中只有圆括号，如果想让括号字符串有效，那么必须做到：

每个右括号 ) 的左边必须有一个左括号 ( 和它匹配。

比如说字符串 ()))(( 中，中间的两个右括号左边就没有左括号匹配，所以这个括号组合是无效的。

那么根据这个思路，我们可以写出算法：

def isValid(str):
    # 待匹配的左括号数量
    left = 0
    for i in range(len(str)):
        if str[i] == '(':
            left += 1
        else:
            # 遇到右括号
            left -= 1
        # 右括号太多
        if left == -1:
            return False
    # 是否所有的左括号都被匹配了
    return left == 0

如果只有圆括号，这样就能正确判断有效性。对于三种括号的情况，我一开始想模仿这个思路，定义三个变量 left1，left2，left3 分别处理每种括号，虽然要多写不少 if else 分支，但是似乎可以解决问题。

但实际上直接照搬这种思路是不行的，比如说只有一个括号的情况下 (()) 是有效的，但是多种括号的情况下， [(]) 显然是无效的。

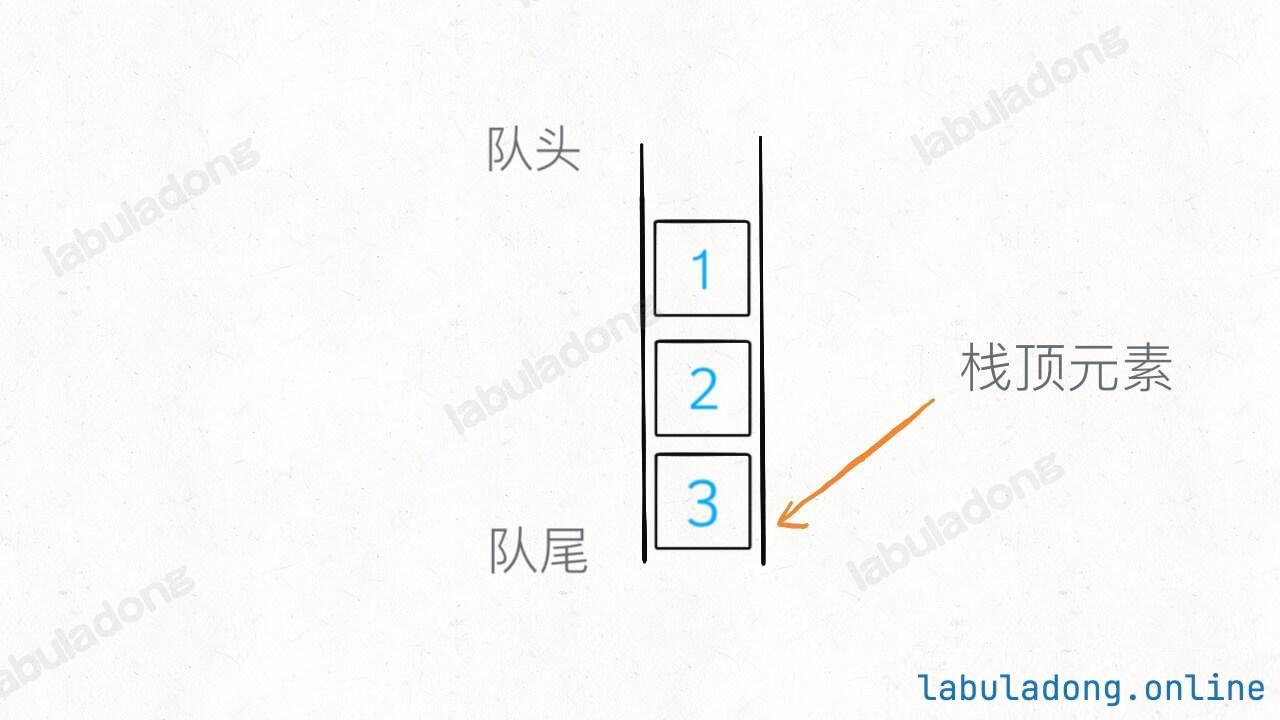
仅仅记录每种左括号出现的次数已经不能做出正确判断了，我们要加大存储的信息量，可以利用栈来模仿类似的思路。栈是一种先进后出的数据结构，处理括号问题的时候尤其有用。

我们这道题就用一个名为 left 的栈代替之前思路中的 left 变量，遇到左括号就入栈，遇到右括号就去栈中寻找最近的左括号，看是否匹配：

class Solution:
    def isValid(self, str: str) -> bool:
        left = []
        for c in str:
            if c in '({[':
                # 字符 c 是左括号，入栈
                left.append(c)
            else:
                # 字符 c 是右括号
                if left and self.leftOf(c) == left[-1]:
                    left.pop()
                else:
                    # 和最近的左括号不匹配
                    return False
        # 是否所有的左括号都被匹配了
        return not left

    def leftOf(self, c: str) -> str:
        if c == '}':
            return '{'
        if c == ')':
            return '('
        return '['

 算法可视化面板

接下来讲另外两个常见的问题，如何通过最小的插入次数将括号变成有效的？

921. 使括号有效的最小添加

先来个简单的，力扣第 921 题「使括号有效的最少添加」：

921. 使括号有效的最少添加 | 力扣 | LeetCode |  🟠

只有满足下面几点之一，括号字符串才是有效的：

• 它是一个空字符串，或者
• 它可以被写成 AB （A 与 B 连接）, 其中 A 和 B 都是有效字符串，或者
• 它可以被写作 (A)，其中 A 是有效字符串。

给定一个括号字符串 s ，在每一次操作中，你都可以在字符串的任何位置插入一个括号

• 例如，如果 s = "()))" ，你可以插入一个开始括号为 "(()))" 或结束括号为 "())))" 。

返回 为使结果字符串 s 有效而必须添加的最少括号数。

示例 1：

输入：s = "())"
输出：1

示例 2：

输入：s = "((("
输出：3

提示：

• 1 <= s.length <= 1000
• s 只包含 '(' 和 ')' 字符。

题目来源：力扣 921. 使括号有效的最少添加。

这其实和前文的判断括号有效性非常类似，我们直接看代码：

这段代码就是最终解法，核心思路是以左括号为基准，通过维护对右括号的需求数 need，来计算最小的插入次数。需要注意两个地方：

1、当 need == -1 的时候意味着什么？

因为只有遇到右括号 ) 的时候才会 need--，need == -1 意味着右括号太多了，所以需要插入左括号。

比如说 s = "))" 这种情况，需要插入 2 个左括号，使得 s 变成 "()()"，才是一个有效括号串。

2、算法为什么返回 res + need？

因为 res 记录的左括号的插入次数，need 记录了右括号的需求，当 for 循环结束后，若 need 不为 0，那么就意味着右括号还不够，需要插入。

比如说 s = "))(" 这种情况，插入 2 个左括号之后，还要再插入 1 个右括号，使得 s 变成 "()()()"，才是一个有效括号串。

以上就是这道题的思路，接下来我们看一道进阶题目，如果左右括号不是 1:1 配对，会出现什么问题呢？

1541. 平衡括号串的最少插入

这是力扣第 1541 题「平衡括号字符串的最少插入次数」：

1541. 平衡括号字符串的最少插入次数 | 力扣 | LeetCode |  🟠

给你一个括号字符串 s ，它只包含字符 '(' 和 ')' 。一个括号字符串被称为平衡的当它满足：

• 任何左括号 '(' 必须对应两个连续的右括号 '))' 。
• 左括号 '(' 必须在对应的连续两个右括号 '))' 之前。

比方说 "())"， "())(())))" 和 "(())())))" 都是平衡的， ")()"， "()))" 和 "(()))" 都是不平衡的。

你可以在任意位置插入字符 '(' 和 ')' 使字符串平衡。

请你返回让 s 平衡的最少插入次数。

示例 1：

输入：s = "(()))"
输出：1
解释：第二个左括号有与之匹配的两个右括号，但是第一个左括号只有一个右括号。我们需要在字符串结尾额外增加一个 ')' 使字符串变成平衡字符串 "(())))" 。

示例 2：

输入：s = "())"
输出：0
解释：字符串已经平衡了。

示例 3：

输入：s = "))())("
输出：3
解释：添加 '(' 去匹配最开头的 '))' ，然后添加 '))' 去匹配最后一个 '(' 。

示例 4：

输入：s = "(((((("
输出：12
解释：添加 12 个 ')' 得到平衡字符串。

示例 5：

输入：s = ")))))))"
输出：5
解释：在字符串开头添加 4 个 '(' 并在结尾添加 1 个 ')' ，字符串变成平衡字符串 "(((())))))))" 。

提示：

• 1 <= s.length <= 10^5
• s 只包含 '(' 和 ')' 。

题目来源：力扣 1541. 平衡括号字符串的最少插入次数。

现在假设 1 个左括号需要匹配 2 个右括号才叫做有效的括号组合，那么给你输入一个括号串 s，请问你如何计算使得 s 有效的最小插入次数呢？

核心思路还是和刚才一样，通过一个 need 变量记录对右括号的需求数，根据 need 的变化来判断是否需要插入。

第一步，我们按照刚才的思路正确维护 need 变量：

def minInsertions(s: str) -> int: 
    # need 记录需右括号的需求量
    res = 0 
    need = 0 
    for i in range(len(s)):
        # 一个左括号对应两个右括号
        if s[i] == '(': 
            need += 2 

        if s[i] == ')': 
            need -= 1 

    return res + need

现在想一想，当 need 为什么值的时候，我们可以确定需要进行插入？

首先，类似第一题，当 need == -1 时，意味着我们遇到一个多余的右括号，显然需要插入一个左括号。

比如说当 s = ")"，我们肯定需要插入一个左括号让 s = "()"，但是由于一个左括号需要两个右括号，所以对右括号的需求量变为 1：

if (s[i] == ')') {
    need--;
    // 说明右括号太多了
    if (need == -1) {
        // 需要插入一个左括号
        res++;
        // 同时，对右括号的需求变为 1
        need = 1;
    }
}

另外，当遇到左括号时，若对右括号的需求量为奇数，需要插入 1 个右括号。因为一个左括号需要两个右括号嘛，右括号的需求必须是偶数，这一点也是本题的难点。

所以遇到左括号时要做如下判断：

if (s[i] == '(') {
    need += 2;
    if (need % 2 == 1) {
        // 插入一个右括号
        res++;
        // 对右括号的需求减一
        need--;
    }
}

综上，我们可以写出正确的代码：

class Solution:
    def minInsertions(self, s: str) -> int:
        # need 记录需右括号的需求量
        res = 0
        need = 0

        for i in range(len(s)):
            # 一个左括号对应两个右括号
            if s[i] == '(':
                need += 2
                if need % 2 == 1:
                    # 插入一个右括号
                    res += 1
                    need -= 1

            if s[i] == ')':
                need -= 1
                # 说明右括号太多了
                if need == -1:
                    # 需要插入一个左括号
                    res += 1
                    # 同时，对右括号的需求变为 1
                    need = 1

        return res + need