【练习】栈的经典习题
考察先进后出性质
对于栈这种数据结构的考察,主要考察先进后出特点的运用,比如表达式运算、括号合法性检测等问题,下面列出几个使用栈的经典场景。
71. 简化路径
71. 简化路径 | 力扣 | LeetCode | 🟠
给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 '/' 开头),请你将其转化为更加简洁的规范路径。
在 Unix 风格的文件系统中,一个点(.)表示当前目录本身;此外,两个点 (..) 表示将目录切换到上一级(指向父目录);两者都可以是复杂相对路径的组成部分。任意多个连续的斜杠(即,'//')都被视为单个斜杠 '/' 。 对于此问题,任何其他格式的点(例如,'...')均被视为文件/目录名称。
请注意,返回的 规范路径 必须遵循下述格式:
- 始终以斜杠
'/'开头。 - 两个目录名之间必须只有一个斜杠
'/'。 - 最后一个目录名(如果存在)不能 以
'/'结尾。 - 此外,路径仅包含从根目录到目标文件或目录的路径上的目录(即,不含
'.'或'..')。
返回简化后得到的 规范路径 。
示例 1:
输入:path = "/home/" 输出:"/home" 解释:注意,最后一个目录名后面没有斜杠。
示例 2:
输入:path = "/../" 输出:"/" 解释:从根目录向上一级是不可行的,因为根目录是你可以到达的最高级。
示例 3:
输入:path = "/home//foo/" 输出:"/home/foo" 解释:在规范路径中,多个连续斜杠需要用一个斜杠替换。
示例 4:
输入:path = "/a/./b/../../c/" 输出:"/c"
提示:
1 <= path.length <= 3000path由英文字母,数字,'.','/'或'_'组成。path是一个有效的 Unix 风格绝对路径。
基本思路
这题比较简单,利用栈先进后出的特性处理上级目录 ..,最后组装化简后的路径即可。
详细题解:
解法代码
class Solution:
def simplifyPath(self, path: str) -> str:
parts = path.split("/")
stk = []
# 借助栈计算最终的文件夹路径
for part in parts:
if part == "" or part == ".":
continue
if part == "..":
if stk:
stk.pop()
continue
stk.append(part)
# 栈中存储的文件夹组成路径
res = ""
while stk:
res = "/" + stk.pop() + res
return res if res else "/"可视化
算法可视化面板
143. 重排链表
143. 重排链表 | 力扣 | LeetCode | 🟠
给定一个单链表 L 的头节点 head ,单链表 L 表示为:
L0 → L1 → … → Ln - 1 → Ln
请将其重新排列后变为:
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例 1:

输入:head = [1,2,3,4] 输出:[1,4,2,3]
示例 2:

输入:head = [1,2,3,4,5] 输出:[1,5,2,4,3]
提示:
- 链表的长度范围为
[1, 5 * 104] 1 <= node.val <= 1000
基本思路
这题的难点在于:一个单链表只能从头部向尾部遍历节点,无法从尾部开始向头部遍历节点。
那么我们可以利用「栈」先进后出的结构特点,按从头到尾的顺序让链表节点入栈,那么出栈顺序就是反过来从尾到头了。
有了这个栈,算法的大致逻辑如下:
ListNode p = head;
while (p != null) {
// 链表尾部的节点
ListNode lastNode = stk.pop();
// 按题目要求拼接
ListNode next = p.next;
p.next = lastNode;
lastNode.next = next;
p = next;
}当然,处理单链表时细节问题比较多,注意操作指针时的顺序,避免操作失误形成环形链表,直接看我的代码注释吧。
详细题解:
解法代码
class Solution:
def reorderList(self, head: ListNode) -> None:
stk = []
# 先把所有节点装进栈里,得到倒序结果
p = head
while p is not None:
stk.append(p)
p = p.next
p = head
while p is not None:
# 链表尾部的节点
lastNode = stk.pop()
next = p.next
if lastNode == next or lastNode.next == next:
# 结束条件,链表节点数为奇数或偶数时均适用
lastNode.next = None
break
p.next = lastNode
lastNode.next = next
p = next可视化
算法可视化面板
类似题目:
20. 有效的括号
20. 有效的括号 | 力扣 | LeetCode | 🟢
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
示例 1:
输入:s = "()" 输出:true
示例 2:
输入:s = "()[]{}"
输出:true
示例 3:
输入:s = "(]" 输出:false
提示:
1 <= s.length <= 104s仅由括号'()[]{}'组成
基本思路
栈是一种先进后出的数据结构,处理括号问题的时候尤其有用。
括号的有效性判断在笔试中和现实中都很常见,比如说我们写的代码,编辑器会检查括号是否正确闭合。而且我们的代码可能会包含三种括号 [](){},判断起来有一点难度。
解决这个问题之前,我们先降低难度,思考一下,如果只有一种括号 (),应该如何判断字符串组成的括号是否有效呢?
假设字符串中只有圆括号,如果想让括号字符串有效,那么必须做到:
每个右括号 ) 的左边必须有一个左括号 ( 和它匹配。
比如说字符串 ()))(( 中,中间的两个右括号左边就没有左括号匹配,所以这个括号组合是无效的。
那么根据这个思路,我们可以写出算法:
boolean isValid(String str) {
// 待匹配的左括号数量
int left = 0;
for (int i = 0; i < str.length(); i++) {
if (str.charAt(i) == '(') {
left++;
} else {
// 遇到右括号
left--;
}
// 右括号太多
if (left == -1)
return false;
}
// 是否所有的左括号都被匹配了
return left == 0;
}如果只有圆括号,这样就能正确判断有效性。对于三种括号的情况,我一开始想模仿这个思路,定义三个变量 left1,left2,left3 分别处理每种括号,虽然要多写不少 if else 分支,但是似乎可以解决问题。
但实际上直接照搬这种思路是不行的,比如说只有一个括号的情况下 (()) 是有效的,但是多种括号的情况下, [(]) 显然是无效的。
仅仅记录每种左括号出现的次数已经不能做出正确判断了,我们要加大存储的信息量,可以利用栈来模仿类似的思路。
我们这道题就用一个名为 left 的栈代替之前思路中的 left 变量,遇到左括号就入栈,遇到右括号就去栈中寻找最近的左括号,看是否匹配。
详细题解:
解法代码
class Solution:
def isValid(self, str: str) -> bool:
left = []
for c in str:
if c in '({[':
# 字符 c 是左括号,入栈
left.append(c)
else:
# 字符 c 是右括号
if left and self.leftOf(c) == left[-1]:
left.pop()
else:
# 和最近的左括号不匹配
return False
# 是否所有的左括号都被匹配了
return not left
def leftOf(self, c: str) -> str:
if c == '}':
return '{'
if c == ')':
return '('
return '['可视化
算法可视化面板
150. 逆波兰表达式求值
150. 逆波兰表达式求值 | 力扣 | LeetCode | 🟠
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为
'+'、'-'、'*'和'/'。 - 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
示例 1:
输入:tokens = ["2","1","+","3","*"] 输出:9 解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = ["4","13","5","/","+"] 输出:6 解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"] 输出:22 解释:该算式转化为常见的中缀算术表达式为: ((10 * (6 / ((9 + 3) * -11))) + 17) + 5 = ((10 * (6 / (12 * -11))) + 17) + 5 = ((10 * (6 / -132)) + 17) + 5 = ((10 * 0) + 17) + 5 = (0 + 17) + 5 = 17 + 5 = 22
提示:
1 <= tokens.length <= 104tokens[i]是一个算符("+"、"-"、"*"或"/"),或是在范围[-200, 200]内的一个整数
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
- 平常使用的算式则是一种中缀表达式,如
( 1 + 2 ) * ( 3 + 4 )。 - 该算式的逆波兰表达式写法为
( ( 1 2 + ) ( 3 4 + ) * )。
逆波兰表达式主要有以下两个优点:
- 去掉括号后表达式无歧义,上式即便写成
1 2 + 3 4 + *也可以依据次序计算出正确结果。 - 适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中
基本思路
逆波兰表达式发明出来就是为了方便计算机运用「栈」进行表达式运算的,其运算规则如下:
按顺序遍历逆波兰表达式中的字符,如果是数字,则放入栈;如果是运算符,则将栈顶的两个元素拿出来进行运算,再将结果放入栈。对于减法和除法,运算顺序别搞反了,栈顶第二个数是被除(减)数。
所以这题很简单,直接按照运算规则借助栈计算表达式结果即可。
详细题解:
解法代码
class Solution:
def evalRPN(self, tokens: List[str]) -> int:
stk = []
for token in tokens:
if token in "+-*/":
# 是个运算符,从栈顶拿出两个数字进行运算,运算结果入栈
a = stk.pop()
b = stk.pop()
if token == "+":
stk.append(a + b)
elif token == "*":
stk.append(a * b)
# 对于减法和除法,顺序别搞反了,第二个数是被除(减)数
elif token == "-":
stk.append(b - a)
elif token == "/":
stk.append(int(b / a)) # Ensure the result is an integer
else:
# 是个数字,直接入栈即可
stk.append(int(token))
# 最后栈中剩下一个数字,即是计算结果
return stk.pop()可视化
算法可视化面板
类似题目:
225. 用队列实现栈
225. 用队列实现栈 | 力扣 | LeetCode | 🟢
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
void push(int x)将元素 x 压入栈顶。int pop()移除并返回栈顶元素。int top()返回栈顶元素。boolean empty()如果栈是空的,返回true;否则,返回false。
注意:
- 你只能使用队列的标准操作 —— 也就是
push to back、peek/pop from front、size和is empty这些操作。 - 你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
示例:
输入: ["MyStack", "push", "push", "top", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 2, 2, false]解释:
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False
提示:
1 <= x <= 9- 最多调用
100次push、pop、top和empty - 每次调用
pop和top都保证栈不为空
进阶:你能否仅用一个队列来实现栈。
基本思路
底层用队列实现栈就比较简单粗暴了,只需要一个队列作为底层数据结构。
底层队列只能向队尾添加元素,所以栈的 pop API 相当于要从队尾取元素:
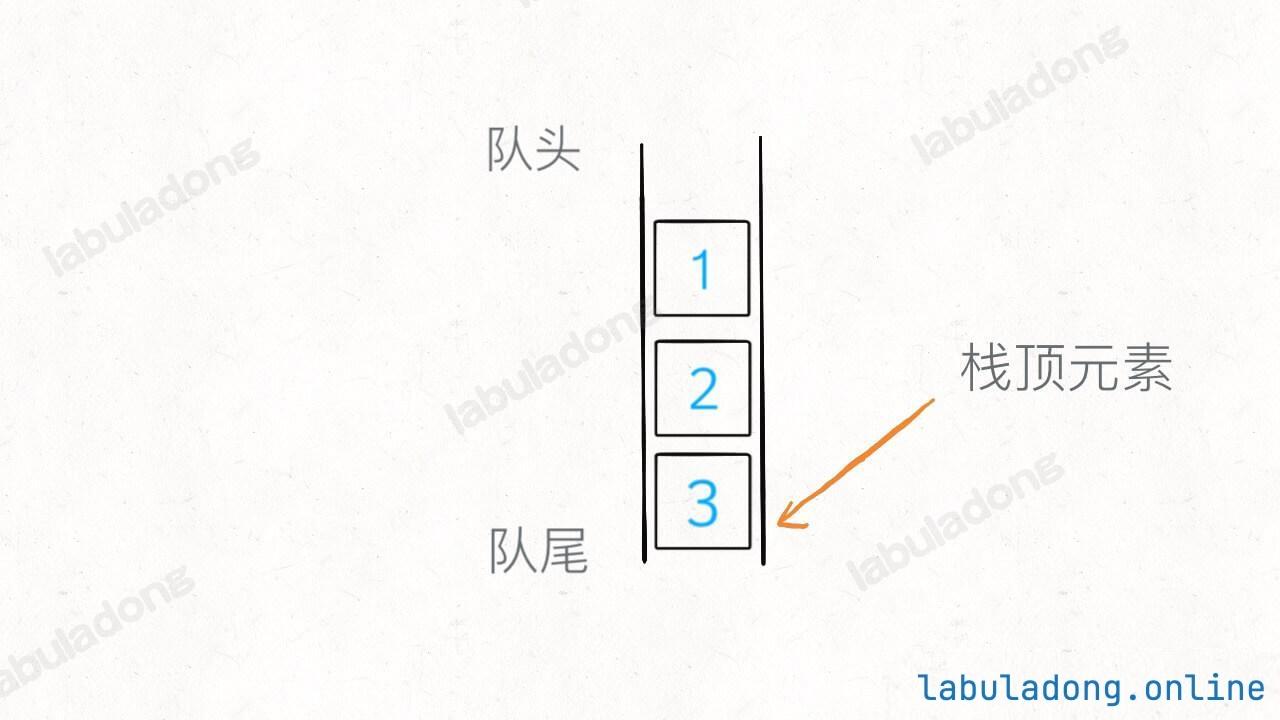
那么最简单的思路就是,把队尾元素前面的所有元素重新塞到队尾,让队尾元素排到队头,这样就可以取出了:

详细题解:
解法代码
from collections import deque
class MyStack:
def __init__(self):
self.q = deque()
self.top_elem = 0
# 将元素 x 压入栈顶
def push(self, x: int) -> None:
# x 是队列的队尾,是栈的栈顶
self.q.append(x)
self.top_elem = x
# 返回栈顶元素
def top(self) -> int:
return self.top_elem
# 删除栈顶的元素并返回
def pop(self) -> int:
size = len(self.q)
# 留下队尾 2 个元素
while size > 2:
self.q.append(self.q.popleft())
size -= 1
# 记录新的队尾元素
self.top_elem = self.q[0]
self.q.append(self.q.popleft())
# 删除之前的队尾元素
return self.q.popleft()
# 判断栈是否为空
def empty(self) -> bool:
return not self.q类似题目:
388. 文件的最长绝对路径
388. 文件的最长绝对路径 | 力扣 | LeetCode | 🟠
假设有一个同时存储文件和目录的文件系统。下图展示了文件系统的一个示例:

这里将 dir 作为根目录中的唯一目录。dir 包含两个子目录 subdir1 和 subdir2 。subdir1 包含文件 file1.ext 和子目录 subsubdir1;subdir2 包含子目录 subsubdir2,该子目录下包含文件 file2.ext 。
在文本格式中,如下所示(⟶表示制表符):
dir ⟶ subdir1 ⟶ ⟶ file1.ext ⟶ ⟶ subsubdir1 ⟶ subdir2 ⟶ ⟶ subsubdir2 ⟶ ⟶ ⟶ file2.ext
如果是代码表示,上面的文件系统可以写为 "dir\n\tsubdir1\n\t\tfile1.ext\n\t\tsubsubdir1\n\tsubdir2\n\t\tsubsubdir2\n\t\t\tfile2.ext" 。'\n' 和 '\t' 分别是换行符和制表符。
文件系统中的每个文件和文件夹都有一个唯一的 绝对路径 ,即必须打开才能到达文件/目录所在位置的目录顺序,所有路径用 '/' 连接。上面例子中,指向 file2.ext 的 绝对路径 是 "dir/subdir2/subsubdir2/file2.ext" 。每个目录名由字母、数字和/或空格组成,每个文件名遵循 name.extension 的格式,其中 name 和 extension由字母、数字和/或空格组成。
给定一个以上述格式表示文件系统的字符串 input ,返回文件系统中 指向 文件 的 最长绝对路径 的长度 。 如果系统中没有文件,返回 0。
示例 1:

输入:input = "dir\n\tsubdir1\n\tsubdir2\n\t\tfile.ext" 输出:20 解释:只有一个文件,绝对路径为 "dir/subdir2/file.ext" ,路径长度 20
示例 2:

输入:input = "dir\n\tsubdir1\n\t\tfile1.ext\n\t\tsubsubdir1\n\tsubdir2\n\t\tsubsubdir2\n\t\t\tfile2.ext" 输出:32 解释:存在两个文件: "dir/subdir1/file1.ext" ,路径长度 21 "dir/subdir2/subsubdir2/file2.ext" ,路径长度 32 返回 32 ,因为这是最长的路径
示例 3:
输入:input = "a" 输出:0 解释:不存在任何文件
示例 4:
输入:input = "file1.txt\nfile2.txt\nlongfile.txt" 输出:12 解释:根目录下有 3 个文件。 因为根目录中任何东西的绝对路径只是名称本身,所以答案是 "longfile.txt" ,路径长度为 12
提示:
1 <= input.length <= 104input可能包含小写或大写的英文字母,一个换行符'\n',一个制表符'\t',一个点'.',一个空格' ',和数字。
基本思路
我觉得这道题还是比较实用的,因为在我做这道题之前,我就思考并解决过这个问题,可以在这里和大家分享下我的使用场景:
你可以看我的 GitHub 仓库中的文章目录,是通过缩进来表示层级的,很类似本题所说的场景。然而我需要把这些目录转化成 HTML 文档,按照文件目录的形式把这些 HTML 部署到 我的网站 上。你看,这是不是就涉及到本题生成文件的绝对路径的问题?
对于这个场景,我当时其实尝试很多可行的办法。但这里我还是写一个最简单直接容易理解的解法吧,那就是用栈来辅助,对于每一个路径,都去维护正确的父路径,从而计算最长路径的长度。具体看代码注释吧。
详细题解:
解法代码
class Solution:
def lengthLongestPath(self, input: str) -> int:
# 这个栈存储之前的父路径。实际上这里只用存父路径的长度就够了,这个优化留给你吧
stack = []
max_len = 0
for part in input.split("\n"):
level = part.rfind("\t") + 1
# 让栈中只保留当前目录的父路径
while level < len(stack):
stack.pop()
stack.append(len(part) - level)
# 如果是文件,就计算路径长度
if "." in part:
total_length = sum(stack) + len(stack) - 1
# 加上父路径的分隔符
max_len = max(max_len, total_length)
return max_len栈的设计题
除了上面几道题,还有一类常考题目是让你设计具备额外功能的栈结构。
155. 最小栈
155. 最小栈 | 力扣 | LeetCode | 🟠
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack()初始化堆栈对象。void push(int val)将元素val推入堆栈。void pop()删除堆栈顶部的元素。int top()获取堆栈顶部的元素。int getMin()获取堆栈中的最小元素。
示例 1:
输入: ["MinStack","push","push","push","getMin","pop","top","getMin"] [[],[-2],[0],[-3],[],[],[],[]]输出:
[null,null,null,null,-3,null,0,-2]解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); –> 返回 -3.
minStack.pop();
minStack.top(); –> 返回 0.
minStack.getMin(); –> 返回 -2.
提示:
-231 <= val <= 231 - 1pop、top和getMin操作总是在 非空栈 上调用push,pop,top, andgetMin最多被调用3 * 104次
基本思路
根据我们之前亲自动手实现的栈,我们知道栈是一种操作受限的数据结构,只能从栈顶插入或弹出元素,所以对于标准的栈来说,如果想实现本题的 getMin 方法,只能老老实实把所有元素弹出来然后找最小值。想提高时间效率,那肯定要通过空间换时间的思路。
不过在具体说解法之前,我想聊一下动态集合中维护最值的问题。这类问题看似简单,但实际上是个很棘手的问题。其实本题就是如下一个场景:
假设你有若干数字,你用一个 min 变量维护了其中的最小值,如果现在给这些数字中添加一个新数字,那么只要比较这个新数字和 min 的大小就可以得出最新的最小值。但如果现在从这些数字钟删除一个数字,你还能用 min 变量得到最小值吗?答案是不能,因为如果这个被删除的数字恰好是最小值,那么新的 min 变量应该更新为第二小的元素对吧,但是我没有记录第二小的元素是多少,所以只能把所有数字重新遍历一遍。
明确了难点再回到本题,就可以对症下药了。删除栈顶元素的时候,不确定新的最小值是多少,但楼下那哥们知道啊,他当时入栈时的最小值,就是现在的最小值呗。
所以这道题的关键就是,每个元素入栈时,还要记下来当前栈中的最小值。比方说,可以用一个额外的栈 minStk 来记录栈中每个元素入栈时的栈中的最小元素是多少,这样每次删除元素时就能快速得到剩余栈中的最小元素了。
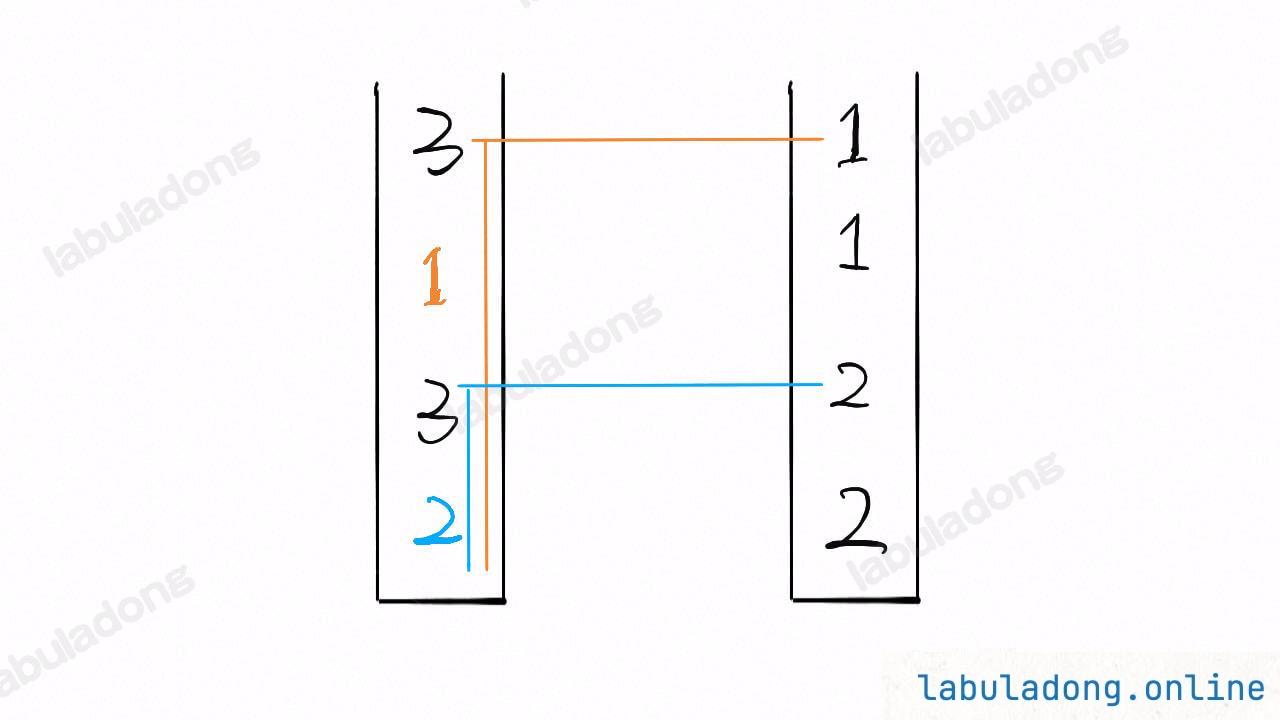
当然,我们还可以做一些优化,减少 minStk 中存储的元素个数,我把原始解法和优化解法都写出来了,供参考。
PS:这道题并不难,但我还是很细致地分析了,希望你深刻理解其中的难点。下一步可以做一下 239. 滑动窗口最大值,请仔细观察和思考,队列结构是如何解决这个难点的。
详细题解:
解法代码
# 原始思路
class MinStack1:
def __init__(self):
# 记录栈中的所有元素
self.stk = []
# 阶段性记录栈中的最小元素
self.minStk = []
def push(self, val: int) -> None:
self.stk.append(val)
# 维护 minStk 栈顶为全栈最小元素
if not self.minStk or val <= self.minStk[-1]:
# 新插入的这个元素就是全栈最小的
self.minStk.append(val)
else:
# 插入的这个元素比较大
self.minStk.append(self.minStk[-1])
def pop(self) -> None:
self.stk.pop()
self.minStk.pop()
def top(self) -> int:
return self.stk[-1]
def getMin(self) -> int:
# minStk 栈顶为全栈最小元素
return self.minStk[-1]
# 优化版
class MinStack:
def __init__(self):
# 记录栈中的所有元素
self.stk = []
# 阶段性记录栈中的最小元素
self.minStk = []
def push(self, val: int) -> None:
self.stk.append(val)
# 维护 minStk 栈顶为全栈最小元素
if not self.minStk or val <= self.minStk[-1]:
# 新插入的这个元素就是全栈最小的
self.minStk.append(val)
def pop(self) -> None:
# 注意 Java 的语言特性,比较 Integer 相等要用 equals 方法
if self.stk[-1] == self.minStk[-1]:
# 弹出的元素是全栈最小的
self.minStk.pop()
self.stk.pop()
def top(self) -> int:
return self.stk[-1]
def getMin(self) -> int:
# minStk 栈顶为全栈最小元素
return self.minStk[-1]类似题目:
895. 最大频率栈
895. 最大频率栈 | 力扣 | LeetCode | 🔴
设计一个类似堆栈的数据结构,将元素推入堆栈,并从堆栈中弹出出现频率最高的元素。
实现 FreqStack 类:
FreqStack()构造一个空的堆栈。void push(int val)将一个整数val压入栈顶。int pop()删除并返回堆栈中出现频率最高的元素。- 如果出现频率最高的元素不只一个,则移除并返回最接近栈顶的元素。
示例 1:
输入: ["FreqStack","push","push","push","push","push","push","pop","pop","pop","pop"], [[],[5],[7],[5],[7],[4],[5],[],[],[],[]] 输出:[null,null,null,null,null,null,null,5,7,5,4] 解释: FreqStack = new FreqStack(); freqStack.push (5);//堆栈为 [5] freqStack.push (7);//堆栈是 [5,7] freqStack.push (5);//堆栈是 [5,7,5] freqStack.push (7);//堆栈是 [5,7,5,7] freqStack.push (4);//堆栈是 [5,7,5,7,4] freqStack.push (5);//堆栈是 [5,7,5,7,4,5] freqStack.pop ();//返回 5 ,因为 5 出现频率最高。堆栈变成 [5,7,5,7,4]。 freqStack.pop ();//返回 7 ,因为 5 和 7 出现频率最高,但7最接近顶部。堆栈变成 [5,7,5,4]。 freqStack.pop ();//返回 5 ,因为 5 出现频率最高。堆栈变成 [5,7,4]。 freqStack.pop ();//返回 4 ,因为 4, 5 和 7 出现频率最高,但 4 是最接近顶部的。堆栈变成 [5,7]。
提示:
0 <= val <= 109push和pop的操作数不大于2 * 104。- 输入保证在调用
pop之前堆栈中至少有一个元素。
基本思路
这种设计数据结构的问题,主要是要搞清楚问题的难点在哪里,然后结合各种基本数据结构的特性,高效实现题目要求的 API。
那么,我们仔细思考一下 push 和 pop 方法,难点如下:
1、每次 pop 时,必须要知道频率最高的元素是什么。
2、如果频率最高的元素有多个,还得知道哪个是最近 push 进来的元素是哪个。
为了实现上述难点,我们要做到以下几点:
1、肯定要有一个变量 maxFreq 记录当前栈中最高的频率是多少。
2、我们得知道一个频率 freq 对应的元素有哪些,且这些元素要有时间顺序。
3、随着 pop 的调用,每个 val 对应的频率会变化,所以还得维持一个映射记录每个 val 对应的 freq。
综上,我们可以先实现 FreqStack 所需的数据结构:
class FreqStack {
// 记录 FreqStack 中元素的最大频率
int maxFreq = 0;
// 记录 FreqStack 中每个 val 对应的出现频率,后文就称为 VF 表
HashMap<Integer, Integer> valToFreq = new HashMap<>();
// 记录频率 freq 对应的 val 列表,后文就称为 FV 表
HashMap<Integer, Stack<Integer>> freqToVals = new HashMap<>();
}其实这有点类似后文 手把手实现 LFU 算法,注意 freqToVals 中 val 列表用一个栈实现,如果一个 freq 对应的元素有多个,根据栈的特点,可以首先取出最近添加的元素。
具体看解法代码吧,要记住在 push 和 pop 方法中同时修改 maxFreq、VF 表、FV 表,否则容易出现 bug。
算法执行过程如下 GIF 所示:

详细题解:
解法代码
class FreqStack:
def __init__(self):
# 记录 FreqStack 中元素的最大频率
self.maxFreq = 0
# 记录 FreqStack 中每个 val 对应的出现频率,后文就称为 VF 表
self.valToFreq = {}
# 记录频率 freq 对应的 val 列表,后文就称为 FV 表
self.freqToVals = {}
def push(self, val: int) -> None:
# 修改 VF 表:val 对应的 freq 加一
freq = self.valToFreq.get(val, 0) + 1
self.valToFreq[val] = freq
# 修改 FV 表:在 freq 对应的列表加上 val
if freq not in self.freqToVals:
self.freqToVals[freq] = []
self.freqToVals[freq].append(val)
# 更新 maxFreq
self.maxFreq = max(self.maxFreq, freq)
def pop(self) -> int:
# 修改 FV 表:pop 出一个 maxFreq 对应的元素 v
vals = self.freqToVals[self.maxFreq]
v = vals.pop()
# 修改 VF 表:v 对应的 freq 减一
self.valToFreq[v] -= 1
# 更新 maxFreq
if not vals:
# 如果 maxFreq 对应的元素空了
self.maxFreq -= 1
return v


