本文是承接 二叉树心法(纲领篇) 的第三篇文章,前文 二叉树心法(构造篇) 带你学习了二叉树构造技巧,本文加大难度,让你对二叉树同时进行「序列化」和「反序列化」。
要说序列化和反序列化,得先从 JSON 数据格式说起。
JSON 的运用非常广泛,比如我们经常将编程语言中的结构体序列化成 JSON 字符串,存入缓存或者通过网络发送给远端服务,消费者接受 JSON 字符串然后进行反序列化,就可以得到原始数据了。
这就是序列化和反序列化的目的,以某种特定格式组织数据,使得数据可以独立于编程语言。
那么假设现在有一棵用 Java 实现的二叉树,我想把它通过某些方式存储下来,然后用 C++ 读取这棵并还原这棵二叉树的结构,怎么办?这就需要对二叉树进行序列化和反序列化了。
零、前/中/后序和二叉树的唯一性
谈具体的题目之前,我们先思考一个问题:什么样的序列化的数据可以反序列化出唯一的一棵二叉树?
比如说,如果给你一棵二叉树的前序遍历结果,你是否能够根据这个结果还原出这棵二叉树呢?
答案是也许可以,也许不可以,具体要看你给的前序遍历结果是否包含空指针的信息。如果包含了空指针,那么就可以唯一确定一棵二叉树,否则就不行。
举例来说,如果我给你这样一个不包含空指针的前序遍历结果 [1,2,3,4,5],那么如下两棵二叉树都是满足这个前序遍历结果的:
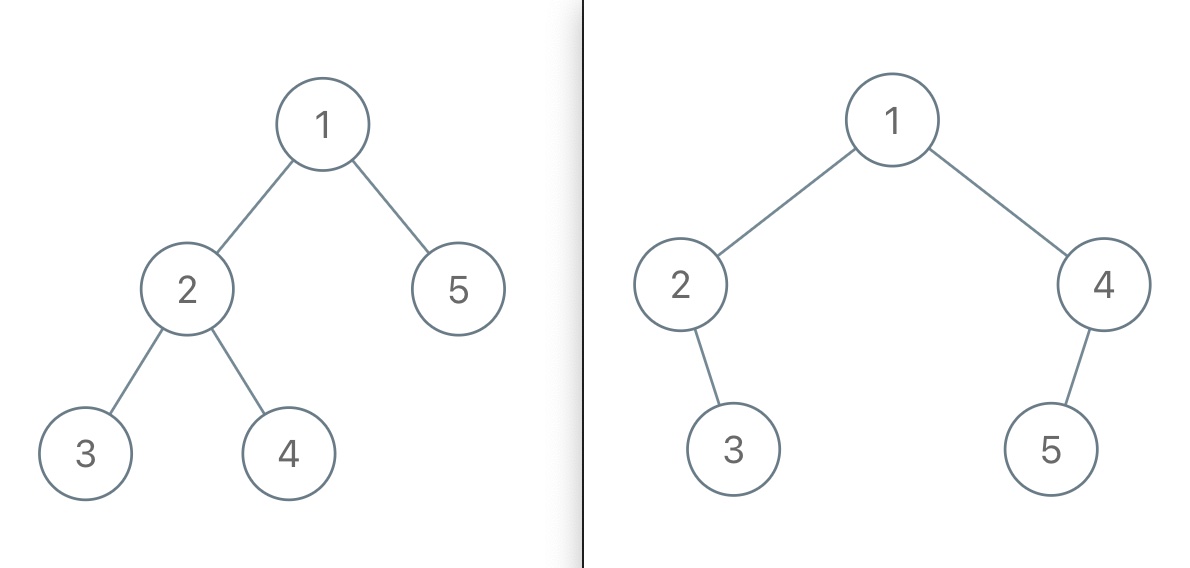
所以给定不包含空指针信息的前序遍历结果,是不能还原出唯一的一棵二叉树的。
但如果我的前序遍历结果包含空指针的信息,那么就能还原出唯一的一棵二叉树了。比如说用 # 表示空指针,上图左侧的二叉树的前序遍历结果就是 [1,2,3,#,#,4,#,#,5,#,#],上图右侧的二叉树的前序遍历结果就是 [1,2,#,3,#,#,4,5,#,#,#],它俩就区分开了。
那么估计就有聪明的小伙伴说了:二叉树心法了。
首先要夸一下这种举一反三的思维,但很不幸,正确答案是,即便你包含了空指针的信息,也只有前序和后序的遍历结果才能唯一还原二叉树,中序遍历结果做不到。
本文后面会具体探讨这个问题,这里只简单说下原因:因为前序/后序遍历的结果中,可以确定根节点的位置,而中序遍历的结果中,根节点的位置是无法确定的。
更直观的,比如如下两棵二叉树显然拥有不同的结构,但它俩的中序遍历结果都是 [#,1,#,1,#],无法区分:
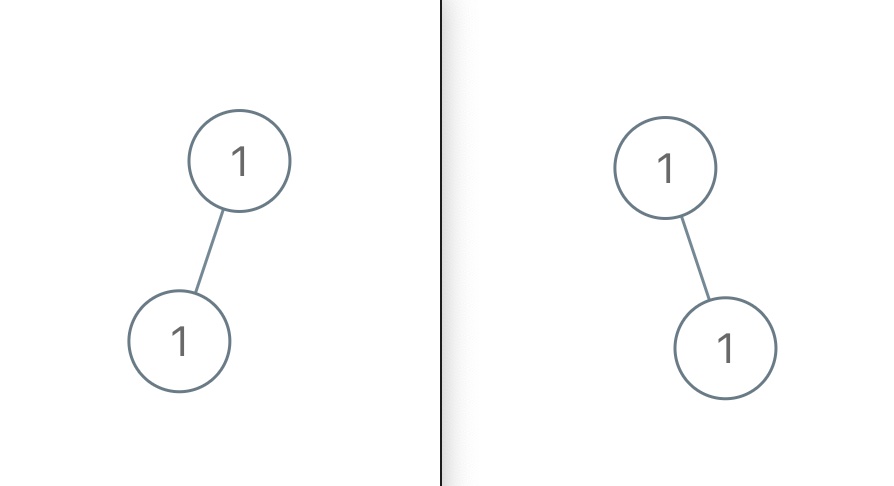
说了这么多,总结下结论,当二叉树中节点的值不存在重复时:
如果你的序列化结果中不包含空指针的信息,且你只给出一种遍历顺序,那么你无法还原出唯一的一棵二叉树。
如果你的序列化结果中不包含空指针的信息,且你会给出两种遍历顺序,分两种情况:
2.1. 如果你给出的是前序和中序,或者后序和中序,那么你可以还原出唯一的一棵二叉树。
2.2. 如果你给出前序和后序,那么你无法还原出唯一的一棵二叉树。
如果你的序列化结果中包含空指针的信息,且你只给出一种遍历顺序,也要分两种情况:
3.1. 如果你给出的是前序或者后序,那么你可以还原出唯一的一棵二叉树。
3.2. 如果你给出的是中序,那么你无法还原出唯一的一棵二叉树。
我在开头提一下这些总结性的认识,可以理解性记忆,之后会遇到一些相关的题目,再回过头来看看这些总结,会有更深的理解,下面看具体的题目吧。
一、题目描述
力扣第 297 题「二叉树的序列化与反序列化」就是给你输入一棵二叉树的根节点 root,要求你实现如下一个类:
class Codec:
# 把一棵二叉树序列化成字符串
def serialize(self, root: TreeNode) -> str:
pass
# 把字符串反序列化成二叉树
def deserialize(self, data: str) -> TreeNode:
pass我们可以用 serialize 方法将二叉树序列化成字符串,用 deserialize 方法将序列化的字符串反序列化成二叉树,至于以什么格式序列化和反序列化,这个完全由你决定。
比如说输入如下这样一棵二叉树:
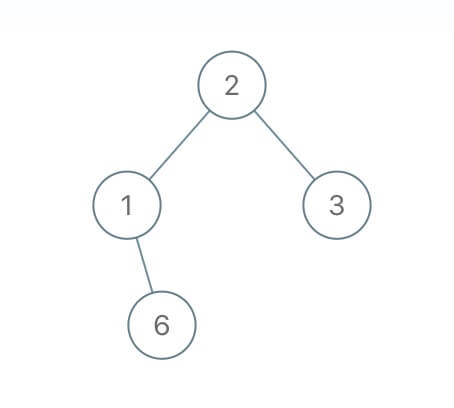
serialize 方法也许会把它序列化成字符串 2,1,#,6,#,#,3,#,#,其中 # 表示 null 指针,那么把这个字符串再输入 deserialize 方法,依然可以还原出这棵二叉树。
也就是说,这两个方法会成对儿使用,你只要保证他俩能够自洽就行了。
想象一下,二叉树是一个二维平面内的结构,而序列化出来的字符串是一个线性的一维结构。所谓的序列化不过就是把结构化的数据「打平」,本质就是在考察二叉树的遍历方式。
二叉树的遍历方式有哪些?递归遍历方式有前序遍历,中序遍历,后序遍历;迭代方式一般是层级遍历。本文就把这些方式都尝试一遍,来实现 serialize 方法和 deserialize 方法。
二、前序遍历解法
前文 二叉树的遍历基础 说过了二叉树的几种遍历方式,在前序位置收集节点,即可获得前序遍历结果:
res = []
def traverse(root):
if root is None:
# 暂且用数字 -1 代表空指针 null
res.append(-1)
return
# ****** 前序位置 ******
res.append(root.val)
# **********************
traverse(root.left)
traverse(root.right)调用 traverse 函数之后,你是否可以立即想出这个 res 列表中元素的顺序是怎样的?比如如下二叉树(# 代表空指针 null),可以直观看出前序遍历做的事情:
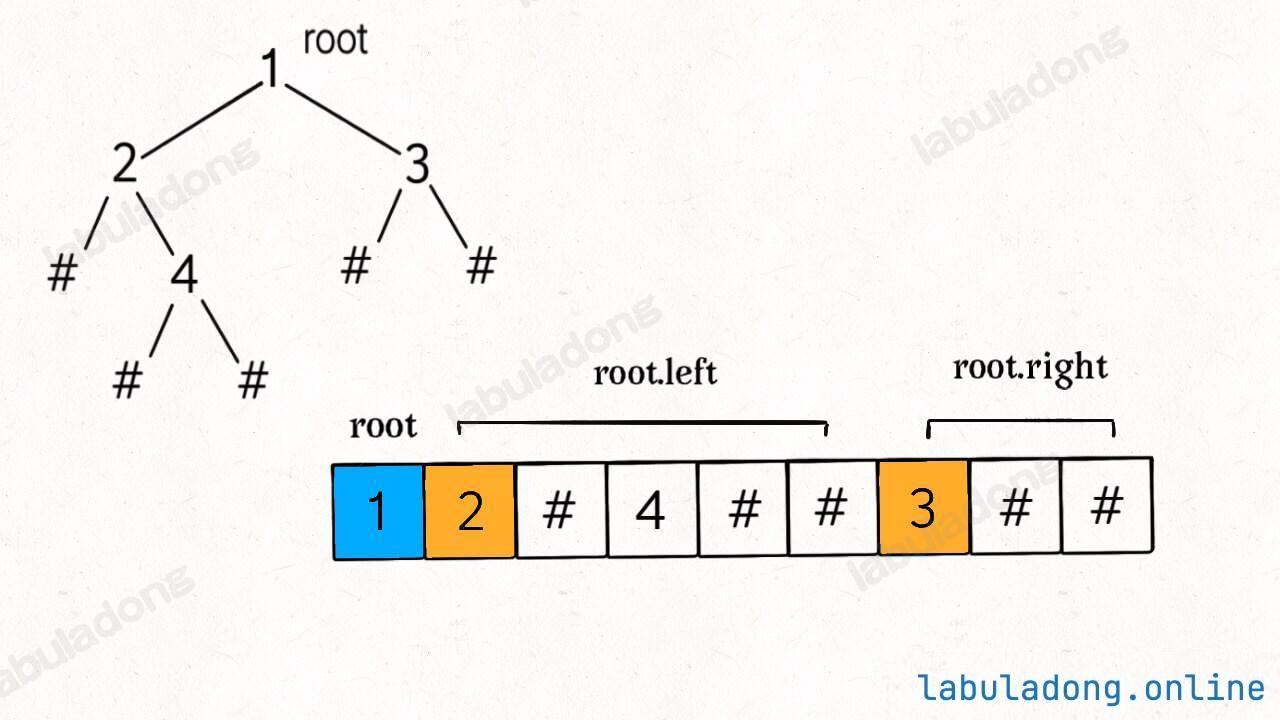
那么 res = [1,2,-1,4,-1,-1,3,-1,-1],这就是将二叉树「打平」到了一个列表中,其中 -1 代表 null。
那么,将二叉树打平到一个字符串中也是完全一样的:
# 代表分隔符的字符
SEP = ","
# 代表 null 空指针的字符
NULL = "#"
# 用于拼接字符串
sb = []
# 将二叉树打平为字符串
def traverse(root, sb):
if root == None:
sb.append(NULL).append(SEP)
return
# ***** 前序位置 *****
sb.append(str(root.val)).append(SEP)
# *******************
traverse(root.left, sb)
traverse(root.right, sb)这段代码依然是收集前序遍历结果,用 , 作为分隔符,用 # 表示空指针 null,调用完 traverse 函数后,sb 中的字符串应该是 1,2,#,4,#,#,3,#,#,。
至此,我们已经可以写出序列化函数 serialize 的代码了:
class Codec:
SEP = ","
NULL = "#"
# 主函数,将二叉树序列化为字符串
def serialize(self, root):
sb = []
self._serialize(root, sb)
return "".join(sb)
# 辅助函数,将二叉树存入 StringBuilder
def _serialize(self, root, sb):
if root is None:
sb.append(self.NULL)
sb.append(self.SEP)
return
# ****** 前序位置 ********
sb.append(str(root.val))
sb.append(self.SEP)
# ***********************
self._serialize(root.left, sb)
self._serialize(root.right, sb)现在,思考一下如何写 deserialize 函数,将字符串反过来构造二叉树。
首先我们可以把字符串转化成列表:
data = "1,2,#,4,#,#,3,#,#,"
nodes = data.split(",")这样,nodes 列表就是二叉树的前序遍历结果,问题转化为:如何通过二叉树的前序遍历结果还原一棵二叉树?
Tip
前文 二叉树心法(构造篇) 说过,至少要得到前、中、后序遍历中的两种互相配合才能还原二叉树。那是因为前文的遍历结果没有记录空指针的信息。这里的 nodes 列表包含了空指针的信息,所以只使用 nodes 列表就可以还原二叉树。
根据我们刚才的分析,nodes 列表就是一棵打平的二叉树:

那么,反序列化过程也是一样,先确定根节点 root,然后遵循前序遍历的规则,递归生成左右子树即可:
class Codec:
SEP = ","
NULL = "#"
# 主函数,将字符串反序列化为二叉树结构
def deserialize(self, data: str) -> TreeNode:
# 将字符串转化成列表
nodes = data.split(self.SEP)
return self._deserialize(nodes)
# 辅助函数,通过 nodes 列表构造二叉树
def _deserialize(self, nodes: List[str]) -> TreeNode:
if not nodes: return None
# ****** 前序位置 *******
# 列表最左侧就是根节点
first = nodes.pop(0)
if first == self.NULL: return None
root = TreeNode(int(first))
# *********************
root.left = self._deserialize(nodes)
root.right = self._deserialize(nodes)
return root我们发现,根据树的递归性质,nodes 列表的第一个元素就是一棵树的根节点,所以只要将列表的第一个元素取出作为根节点,剩下的交给递归函数去解决即可。
三、后序遍历解法
二叉树的后序遍历框架:
def traverse(root: TreeNode) -> None:
if root is None:
return
traverse(root.left)
traverse(root.right)
# 后序位置的代码明白了前序遍历的解法,后序遍历就比较容易理解了。serialize 序列化方法非常容易实现,只需要稍微修改前文的 _serialize辅助方法即可:
# 辅助函数,将二叉树存入 StringBuilder
def _serialize(root, sb):
if root is None:
sb.append(NULL).append(SEP)
return
_serialize(root.left, sb)
_serialize(root.right, sb)
# ****** 后序位置 ********
sb.append(root.val).append(SEP)
# ***********************我们把对 StringBuilder 的拼接操作放到了后序遍历的位置,后序遍历导致结果的顺序发生变化:
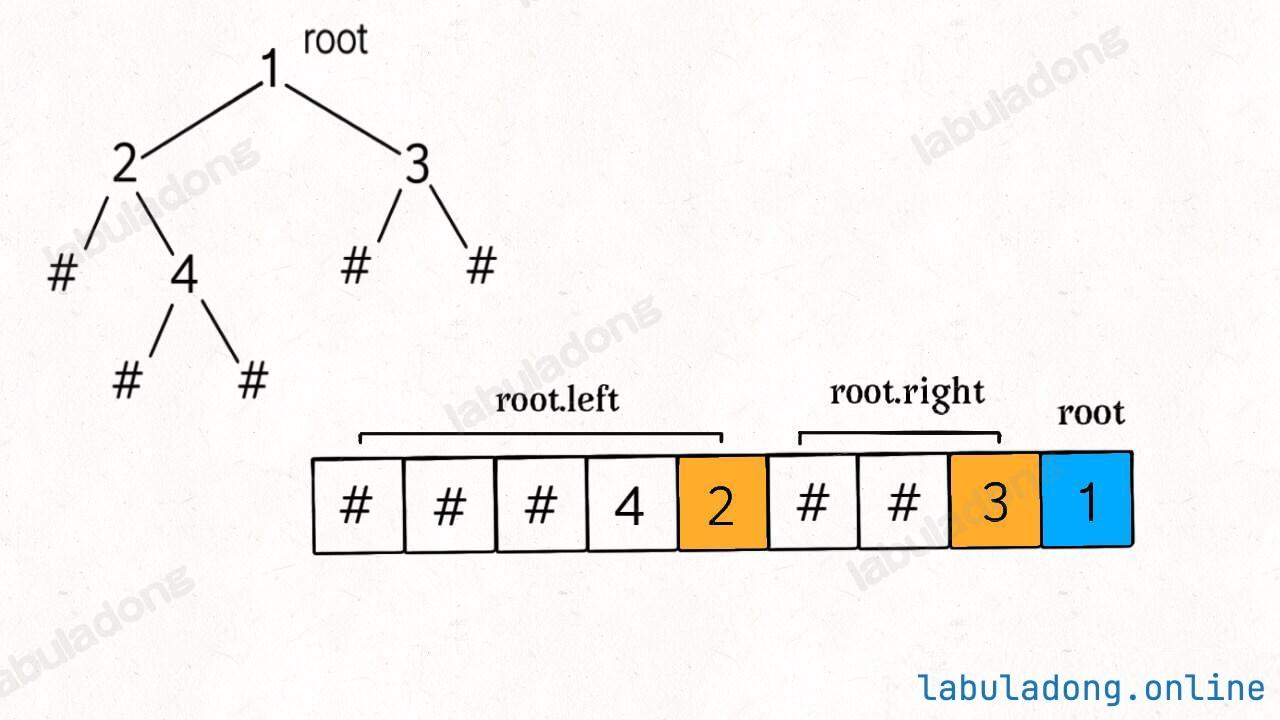
关键点在于,如何实现后序遍历的 deserialize 方法呢?是不是也简单地将反序列化的关键代码无脑放到后序遍历的位置就行了呢:
# 辅助函数,通过 nodes 列表构造二叉树
def deserialize(nodes):
if not nodes:
return None
root.left = deserialize(nodes)
root.right = deserialize(nodes)
# 后序位置
first = nodes.pop(0)
if first == 'NULL':
return None
root = TreeNode(int(first))
return root显然上述代码是错误的,变量都没声明呢,就开始用了?生搬硬套肯定是行不通的,回想刚才我们前序遍历方法中的 deserialize 方法,第一件事情在做什么?
deserialize 方法首先寻找 root 节点的值,然后递归计算左右子节点。那么我们这里也应该顺着这个基本思路走,后序遍历中,root 节点的值能不能找到?
再看一眼刚才的图:

在后序遍历结果中,root 的值是列表的最后一个元素。我们应该从后往前取出列表元素,先用最后一个元素构造 root,然后递归调用生成 root 的左右子树。
注意,根据上图,从后往前在 nodes 列表中取元素,一定要先构造 root.right 子树,后构造 root.left 子树。
看完整代码:
class Codec:
SEP = ","
NULL = "#"
# 主函数,将二叉树序列化为字符串
def serialize(self, root):
sb = []
self._serialize(root, sb)
return ''.join(sb)
def _serialize(self, root, sb):
if root is None:
sb.append(self.NULL)
sb.append(self.SEP)
return
self._serialize(root.left, sb)
self._serialize(root.right, sb)
# ****** 后序位置 ********
sb.append(str(root.val))
sb.append(self.SEP)
# ***********************
# 主函数,将字符串反序列化为二叉树结构
def deserialize(self, data):
# 将分割结果中的空字符串过滤掉
nodes = [x for x in data.split(self.SEP) if x]
return self._deserialize(nodes)
# 辅助函数,通过 nodes 列表构造二叉树
def _deserialize(self, nodes):
if nodes == []:
return None
# 从后往前取出元素
last = nodes.pop()
if last == self.NULL or last == "":
return None
root = TreeNode(int(last))
# 先构造右子树,后构造左子树
root.right = self._deserialize(nodes)
root.left = self._deserialize(nodes)
return root至此,后序遍历实现的序列化、反序列化方法也都实现了。
四、中序遍历解法
先说结论,中序遍历的方式行不通,因为无法实现反序列化方法 deserialize。
序列化方法 serialize 依然容易,只要把辅助函数 _serialize 中的字符串的拼接操作放到中序遍历的位置就行了:
# 辅助函数,将二叉树存入 StringBuilder
def serialize(root: 'TreeNode', sb: 'List[str]') -> None:
if root == None:
sb.append(NULL)
sb.append(SEP)
return
serialize(root.left, sb)
# ******* 中序位置 *******
sb.append(str(root.val))
sb.append(SEP)
# ***********************
serialize(root.right, sb)但是,我们刚才说了,要想实现反序列方法,首先要构造 root 节点。前序遍历得到的 nodes 列表中,第一个元素是 root 节点的值;后序遍历得到的 nodes 列表中,最后一个元素是 root 节点的值。
你看上面这段中序遍历的代码,root 的值被夹在两棵子树的中间,也就是在 nodes 列表的中间,我们不知道确切的索引位置,所以无法找到 root 节点,也就无法进行反序列化。
五、层级遍历解法
先写出 二叉树遍历基础 中的层级遍历代码框架:
def traverse(root):
if root is None:
return
# 初始化队列,将 root 加入队列
q = [root]
while q:
sz = len(q)
for i in range(sz):
# 层级遍历代码位置
cur = q.pop(0)
print(cur.val)
# *************
if cur.left:
q.append(cur.left)
if cur.right:
q.append(cur.right)上述代码是标准的二叉树层级遍历框架,从上到下,从左到右打印每一层二叉树节点的值,可以看到,队列 q 中不会存在 null 指针。
不过我们在反序列化的过程中是需要记录空指针 null 的,所以可以把标准的层级遍历框架略作修改:
from collections import deque
def traverse(root):
if not root:
return
# 初始化队列,将 root 加入队列
q = deque([root])
while q:
sz = len(q)
for _ in range(sz):
cur = q.popleft()
# 层级遍历代码位置
if cur is None:
continue
print(cur.val)
# **************
q.append(cur.left)
q.append(cur.right)这样也可以完成层级遍历,只不过我们把对空指针的检验从「将元素加入队列」的时候改成了「从队列取出元素」的时候。
那么我们完全仿照这个框架即可写出序列化方法:
class Codec:
SEP = ","
NULL = "#"
# 将二叉树序列化为字符串
def serialize(self, root):
if root is None:
return ""
# 初始化队列,将 root 加入队列
queue = [root]
res = []
while queue:
sz = len(queue)
for i in range(sz):
cur = queue.pop(0)
# 层级遍历代码位置
if cur is None:
res.append(self.NULL)
res.append(self.SEP)
continue
res.append(str(cur.val))
res.append(self.SEP)
# ***************
queue.append(cur.left)
queue.append(cur.right)
return Codec.SEP.join(res)层级遍历序列化得出的结果如下图:
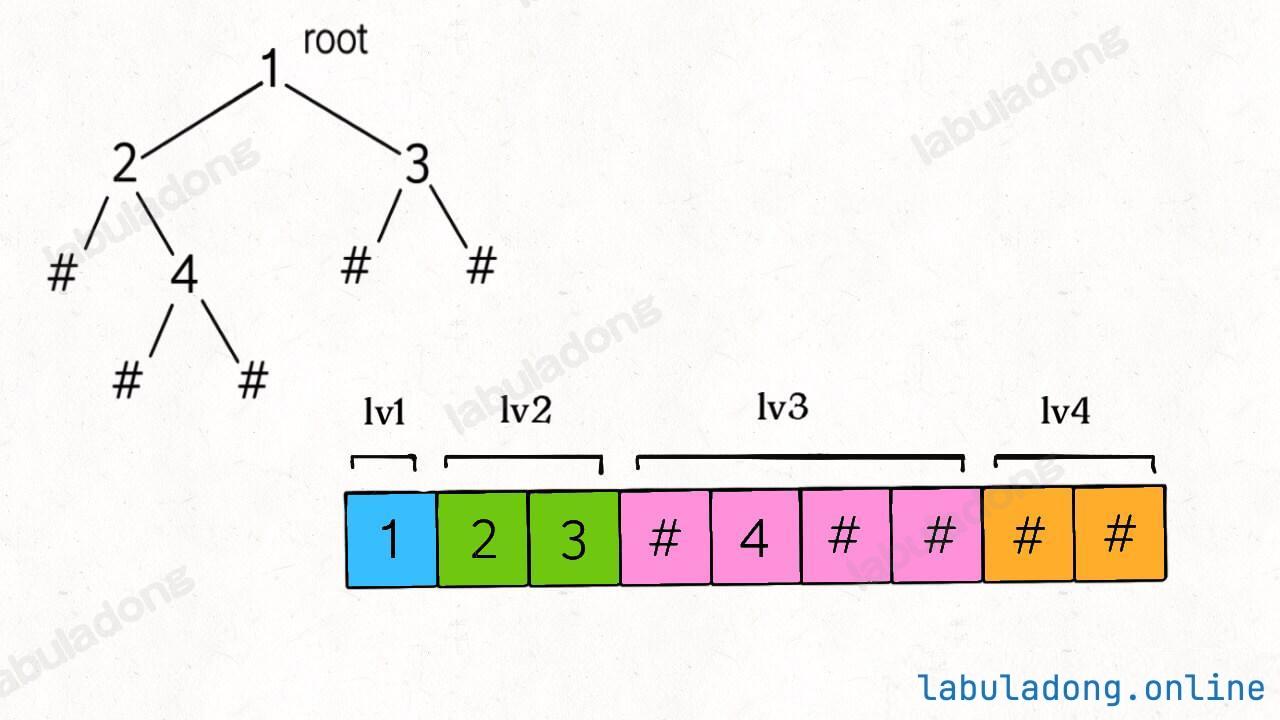
可以看到,每一个非空节点都会对应两个子节点,那么反序列化的思路也是用队列进行层级遍历,同时用索引 index 记录对应子节点的位置:
from collections import deque
class Codec:
SEP = ","
NULL = "#"
# 将字符串反序列化为二叉树结构
def deserialize(self, data: str):
if data == "":
return None
# 将分割结果中的空字符串过滤掉
nodes = [x for x in data.split(self.SEP) if x]
# 第一个元素就是 root 的值
root = TreeNode(int(nodes[0]))
# 队列 q 记录父节点,将 root 加入队列
q = deque([root])
# index 变量记录正在序列化的节点在数组中的位置
index = 1
while q:
sz = len(q)
for i in range(sz):
parent = q.popleft()
# 为父节点构造左侧子节点
left = nodes[index]
index += 1
if left != self.NULL:
parent.left = TreeNode(int(left))
q.append(parent.left)
# 为父节点构造右侧子节点
right = nodes[index]
index += 1
if right != self.NULL:
parent.right = TreeNode(int(right))
q.append(parent.right)
return root不难发现,这个反序列化的代码逻辑也是标准的二叉树层级遍历的代码衍生出来的。我们的函数通过 nodes[index] 来计算左右子节点,接到父节点上并加入队列,一层一层地反序列化出来一棵二叉树。
二叉搜索树心法(特性篇)
本文讲解的例题
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 1038. Binary Search Tree to Greater Sum Tree | 1038. 从二叉搜索树到更大和树 | 🟠 |
| 230. Kth Smallest Element in a BST | 230. 二叉搜索树中第K小的元素 | 🟠 |
| 538. Convert BST to Greater Tree | 538. 把二叉搜索树转换为累加树 | 🟠 |
前置知识
阅读本文前,你需要先学习:
前文手把手带你刷二叉树已经写了 思维篇,构造篇,后序篇 和 序列化篇。
今天开启二叉搜索树(Binary Search Tree,后文简写 BST)的系列文章,手把手带你刷 BST。
首先,BST 的特性大家应该都很熟悉了(详见基础知识章节的 二叉树基础):
1、对于 BST 的每一个节点 node,左子树节点的值都比 node 的值要小,右子树节点的值都比 node 的值大。
2、对于 BST 的每一个节点 node,它的左侧子树和右侧子树都是 BST。
二叉搜索树并不算复杂,但我觉得它可以算是数据结构领域的半壁江山,直接基于 BST 的数据结构有 AVL 树,红黑树等等,拥有了自平衡性质,可以提供 logN 级别的增删查改效率;还有 B+ 树,线段树等结构都是基于 BST 的思想来设计的。
从做算法题的角度来看 BST,除了它的定义,还有一个重要的性质:BST 的中序遍历结果是有序的(升序)。
也就是说,如果输入一棵 BST,以下代码可以将 BST 中每个节点的值升序打印出来:
def traverse(root):
if not root:
return
traverse(root.left)
# 中序遍历代码位置
print(root.val)
traverse(root.right)那么根据这个性质,我们来做两道算法题。
寻找第 K 小的元素
这是力扣第 230 题「二叉搜索树中第 K 小的元素」,看下题目:
230. 二叉搜索树中第K小的元素 | 力扣
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 小的元素(从 1 开始计数)。
示例 1:

输入:root = [3,1,4,null,2], k = 1 输出:1
示例 2:

输入:root = [5,3,6,2,4,null,null,1], k = 3 输出:3
提示:
- 树中的节点数为
n。 1 <= k <= n <= 1040 <= Node.val <= 104
进阶:如果二叉搜索树经常被修改(插入/删除操作)并且你需要频繁地查找第 k 小的值,你将如何优化算法?
这个需求很常见吧,一个直接的思路就是升序排序,然后找第 k 个元素呗。BST 的中序遍历其实就是升序排序的结果,找第 k 个元素肯定不是什么难事。
按照这个思路,可以直接写出代码:
class Solution:
def __init__(self):
# 记录结果
self.res = 0
# 记录当前元素的排名
self.rank = 0
def kthSmallest(self, root: TreeNode, k: int) -> int:
# 利用 BST 的中序遍历特性
self.traverse(root, k)
return self.res
def traverse(self, root, k):
if not root:
return
self.traverse(root.left, k)
# 中序代码位置
self.rank += 1
if k == self.rank:
# 找到第 k 小的元素
self.res = root.val
return
self.traverse(root.right, k)算法可视化面板
这道题就做完了,不过呢,还是要多说几句,因为这个解法并不是最高效的解法,而是仅仅适用于这道题。
我们后文 高效计算数据流的中位数 中就提过今天的这个问题:
Info
如果让你实现一个在二叉搜索树中通过排名计算对应元素的方法 select(int k),你会怎么设计?
如果按照我们刚才说的方法,利用「BST 中序遍历就是升序排序结果」这个性质,每次寻找第 k 小的元素都要中序遍历一次,最坏的时间复杂度是 O(N)O(N),N 是 BST 的节点个数。
要知道 BST 性质是非常牛逼的,像红黑树这种改良的自平衡 BST,增删查改都是 O(logN)O(log**N) 的复杂度,让你算一个第 k 小元素,时间复杂度竟然要 O(N)O(N),有点低效了。
所以说,计算第 k 小元素,最好的算法肯定也是对数级别的复杂度,不过这个依赖于 BST 节点记录的信息有多少。
我们想一下 BST 的操作为什么这么高效?就拿搜索某一个元素来说,BST 能够在对数时间找到该元素的根本原因还是在 BST 的定义里,左子树小右子树大嘛,所以每个节点都可以通过对比自身的值判断去左子树还是右子树搜索目标值,从而避免了全树遍历,达到对数级复杂度。
那么回到这个问题,想找到第 k 小的元素,或者说找到排名为 k 的元素,如果想达到对数级复杂度,关键也在于每个节点得知道他自己排第几。
比如说你让我查找排名为 k 的元素,当前节点知道自己排名第 m,那么我可以比较 m 和 k 的大小:
1、如果 m == k,显然就是找到了第 k 个元素,返回当前节点就行了。
2、如果 k < m,那说明排名第 k 的元素在左子树,所以可以去左子树搜索第 k 个元素。
3、如果 k > m,那说明排名第 k 的元素在右子树,所以可以去右子树搜索第 k - m - 1 个元素。
这样就可以将时间复杂度降到 O(logN)O(log**N) 了。
那么,如何让每一个节点知道自己的排名呢?
这就是我们之前说的,需要在二叉树节点中维护额外信息。每个节点需要记录,以自己为根的这棵二叉树有多少个节点。
也就是说,我们 TreeNode 中的字段应该如下:
class TreeNode:
def __init__(self):
self.val = None
# 以该节点为根的树的节点总数
self.size = None
self.left = None
self.right = None有了 size 字段,外加 BST 节点左小右大的性质,对于每个节点 node 就可以通过 node.left 推导出 node 的排名,从而做到我们刚才说到的对数级算法。
当然,size 字段需要在增删元素的时候需要被正确维护,力扣提供的 TreeNode 是没有 size 这个字段的,所以我们这道题就只能利用 BST 中序遍历的特性实现了,但是我们上面说到的优化思路是 BST 的常见操作,还是有必要理解的。
BST 转化累加树
力扣第 538 题和 1038 题都是这道题,完全一样,你可以把它们一块做掉。看下题目:
538. 把二叉搜索树转换为累加树 | 力扣
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
注意:本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同
示例 1:

输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1] 输出:[1,null,1]
示例 3:
输入:root = [1,0,2] 输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1] 输出:[7,9,4,10]
提示:
- 树中的节点数介于
0和104之间。 - 每个节点的值介于
-104和104之间。 - 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
题目应该不难理解,比如图中的节点 5,转化成累加树的话,比 5 大的节点有 6,7,8,加上 5 本身,所以累加树上这个节点的值应该是 5+6+7+8=26。
我们需要把 BST 转化成累加树,函数签名如下:
def convertBST(root: TreeNode) -> TreeNode:按照二叉树的通用思路,需要思考每个节点应该做什么,但是这道题上很难想到什么思路。
BST 的每个节点左小右大,这似乎是一个有用的信息,既然累加和是计算大于等于当前值的所有元素之和,那么每个节点都去计算右子树的和,不就行了吗?
这是不行的。对于一个节点来说,确实右子树都是比它大的元素,但问题是它的父节点也可能是比它大的元素呀?这个没法确定的,我们又没有触达父节点的指针,所以二叉树的通用思路在这里用不了。
此路不通,我们不妨换一个思路,还是利用 BST 的中序遍历特性。
刚才我们说了 BST 的中序遍历代码可以升序打印节点的值,那如果我想降序打印节点的值怎么办?
很简单,只要把递归顺序改一下,先遍历右子树,后遍历左子树就行了:
def traverse(root):
if root is None:
return
# 先递归遍历右子树
traverse(root.right)
# 中序遍历代码位置
print(root.val)
# 后递归遍历左子树
traverse(root.left)这段代码可以降序打印 BST 节点的值,如果维护一个外部累加变量 sum,然后把 sum 赋值给 BST 中的每一个节点,不就将 BST 转化成累加树了吗?
看下代码就明白了:
class Solution:
def __init__(self):
# 记录累加和
self.sum = 0
def convertBST(self, root):
self.traverse(root)
return root
def traverse(self, root):
if root is None:
return
self.traverse(root.right)
# 维护累加和
self.sum += root.val
# 将 BST 转化成累加树
root.val = self.sum
self.traverse(root.left)算法可视化面板
这道题就解决了,核心还是 BST 的中序遍历特性,只不过我们修改了递归顺序,降序遍历 BST 的元素值,从而契合题目累加树的要求。
简单总结下吧,BST 相关的问题,要么利用 BST 左小右大的特性提升算法效率,要么利用中序遍历的特性满足题目的要求,也就这么些事儿吧。
二叉搜索树心法(基操篇)
本文讲解的例题
我们前文 二叉搜索树心法(特性篇) 介绍了 BST 的基本特性,还利用二叉搜索树「中序遍历有序」的特性来解决了几道题目,本文来实现 BST 的基础操作:判断 BST 的合法性、增、删、查。其中「删」和「判断合法性」略微复杂。
BST 的基础操作主要依赖「左小右大」的特性,可以在二叉树中做类似二分搜索的操作,寻找一个元素的效率很高。比如下面这就是一棵合法的二叉树:
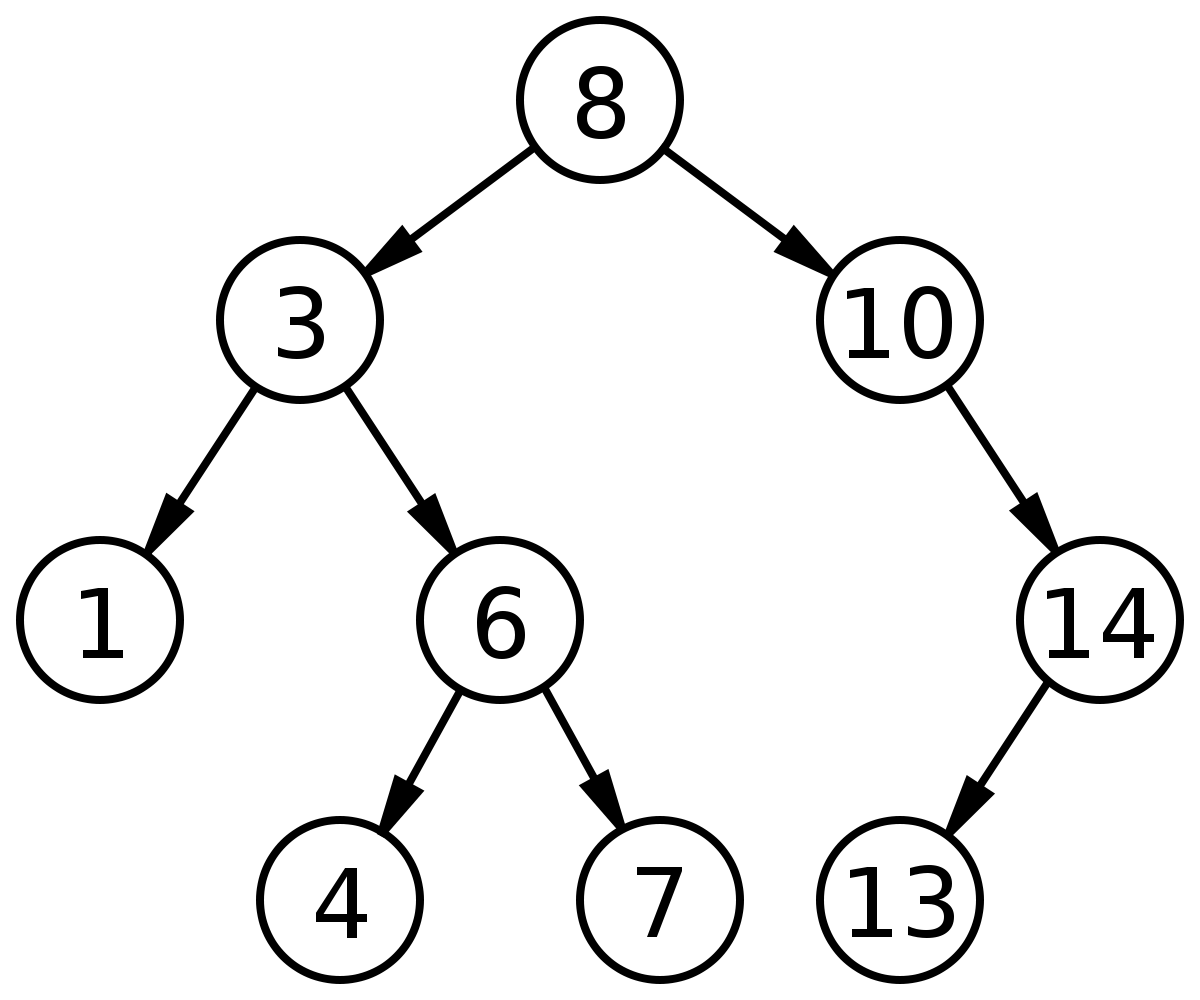
对于 BST 相关的问题,你可能会经常看到类似下面这样的代码逻辑:
def BST(root: TreeNode, target: int) -> None:
if root.val == target:
# 找到目标,做点什么
if root.val < target:
BST(root.right, target)
if root.val > target:
BST(root.left, target)这个代码框架其实和二叉树的遍历框架差不多,无非就是利用了 BST 左小右大的特性而已。接下来看下 BST 这种结构的基础操作是如何实现的。
一、判断 BST 的合法性
力扣第 98 题「验证二叉搜索树」就是让你判断输入的 BST 是否合法:
98. 验证二叉搜索树 | 力扣
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:

输入:root = [2,1,3] 输出:true
示例 2:

输入:root = [5,1,4,null,null,3,6] 输出:false 解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
- 树中节点数目范围在
[1, 104]内 -231 <= Node.val <= 231 - 1
注意,这里是有坑的哦。按照 BST 左小右大的特性,每个节点想要判断自己是否是合法的 BST 节点,要做的事不就是比较自己和左右孩子吗?感觉应该这样写代码:
def isValidBST(root: TreeNode) -> bool:
if root is None:
return True
# root 的左边应该更小
if root.left is not None and root.left.val >= root.val:
return False
# root 的右边应该更大
if root.right is not None and root.right.val <= root.val:
return False
return isValidBST(root.left) and isValidBST(root.right)但是这个算法出现了错误,BST 的每个节点应该要小于右边子树的所有节点,下面这个二叉树显然不是 BST,因为节点 7 的左子树中有一个节点 8,但是我们的算法会把它判定为合法 BST:
7418910
错误的原因在于,对于每一个节点 root,代码值检查了它的左右孩子节点是否符合左小右大的原则;但是根据 BST 的定义,root 的整个左子树都要小于 root.val,整个右子树都要大于 root.val。
问题是,对于某一个节点 root,他只能管得了自己的左右子节点,怎么把 root 的约束传递给左右子树呢?请看正确的代码:
class Solution:
def isValidBST(self, root: TreeNode) -> bool:
return self._isValidBST(root, None, None)
# 定义:该函数返回 root 为根的子树的所有节点是否满足 max.val > root.val > min.val
def _isValidBST(self, root: TreeNode, min: TreeNode, max: TreeNode) -> bool:
# base case
if root is None:
return True
# 若 root.val 不符合 max 和 min 的限制,说明不是合法 BST
if min is not None and root.val <= min.val:
return False
if max is not None and root.val >= max.val:
return False
# 根据定义,限定左子树的最大值是 root.val,右子树的最小值是 root.val
return self._isValidBST(root.left, min, root) and self._isValidBST(root.right, root, max)算法可视化面板
我们通过使用辅助函数,增加函数参数列表,在参数中携带额外信息,将这种约束传递给子树的所有节点,这也是二叉树算法的一个小技巧吧。
在 BST 中搜索元素
力扣第 700 题「二叉搜索树中的搜索」就是让你在 BST 中搜索值为 target 的节点,函数签名如下:
def searchBST(root: TreeNode, target: int) -> TreeNode:如果是在一棵普通的二叉树中寻找,可以这样写代码:
def searchBST(root, target):
if not root:
return None
if root.val == target:
return root
# 当前节点没找到就递归地去左右子树寻找
left = searchBST(root.left, target)
right = searchBST(root.right, target)
return left if left else right这样写完全正确,但这段代码相当于穷举了所有节点,适用于所有二叉树。那么应该如何充分利用 BST 的特殊性,把「左小右大」的特性用上?
很简单,其实不需要递归地搜索两边,类似二分查找思想,根据 target 和 root.val 的大小比较,就能排除一边。我们把上面的思路稍稍改动:
# 定义:在以 root 为根的 BST 中搜索值为 target 的节点,返回该节点
def searchBST(root: TreeNode, target: int) -> TreeNode:
# 如果二叉树为空,直接返回
if not root:
return None
# 去左子树搜索
if root.val > target:
return searchBST(root.left, target)
# 去右子树搜索
if root.val < target:
return searchBST(root.right, target)
# 当前节点就是目标值
return root算法可视化面板
在 BST 中插入一个数
对数据结构的操作无非遍历 + 访问,遍历就是「找」,访问就是「改」。具体到这个问题,插入一个数,就是先找到插入位置,然后进行插入操作。
因为 BST 一般不会存在值重复的节点,所以我们一般不会在 BST 中插入已存在的值。下面的代码都默认不会向 BST 中插入已存在的值。
上一个问题,我们总结了 BST 中的遍历框架,就是「找」的问题。直接套框架,加上「改」的操作即可。
一旦涉及「改」,就类似二叉树的构造问题,函数要返回 TreeNode 类型,并且要对递归调用的返回值进行接收。
力扣第 701 题「二叉搜索树中的插入操作」就是这个问题:
701. 二叉搜索树中的插入操作 | 力扣
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例 1:

输入:root = [4,2,7,1,3], val = 5 输出:[4,2,7,1,3,5] 解释:另一个满足题目要求可以通过的树是:
示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25 输出:[40,20,60,10,30,50,70,null,null,25]
示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5 输出:[4,2,7,1,3,5]
提示:
- 树中的节点数将在
[0, 104]的范围内。 -108 <= Node.val <= 108- 所有值
Node.val是 独一无二 的。 -108 <= val <= 108- 保证
val在原始BST中不存在。
直接看解法代码吧,可以结合注释和可视化面板的来理解:
# 定义:在以 root 为根的 BST 中插入 val 节点,返回插入后的根节点
class Solution:
def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
if not root:
# 找到空位置插入新节点
return TreeNode(val)
# 去右子树找插入位置
if root.val < val:
root.right = self.insertIntoBST(root.right, val)
# 去左子树找插入位置
if root.val > val:
root.left = self.insertIntoBST(root.left, val)
# 返回 root,上层递归会接收返回值作为子节点
return root算法可视化面板
三、在 BST 中删除一个数
力扣第 450 题「删除二叉搜索树中的节点」就是让你在 BST 中删除一个值为 key 的节点:
450. 删除二叉搜索树中的节点 | 力扣
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
示例 1:

输入:root = [5,3,6,2,4,null,7], key = 3 输出:[5,4,6,2,null,null,7] 解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。 一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。 另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0 输出: [5,3,6,2,4,null,7] 解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0 输出: []
提示:
- 节点数的范围
[0, 104]. -105 <= Node.val <= 105- 节点值唯一
root是合法的二叉搜索树-105 <= key <= 105
进阶: 要求算法时间复杂度为 O(h),h 为树的高度。
这个问题稍微复杂,跟插入操作类似,先「找」再「改」,先把框架写出来再说:
def deleteNode(root: TreeNode, key: int) -> TreeNode:
if root.val == key:
# 找到啦,进行删除
elif root.val > key:
# 去左子树找
root.left = deleteNode(root.left, key)
elif root.val < key:
# 去右子树找
root.right = deleteNode(root.right, key)
return root找到目标节点了,比方说是节点 A,如何删除这个节点,这是难点。因为删除节点的同时不能破坏 BST 的性质。有三种情况,用图片来说明。
情况 1:A 恰好是末端节点,两个子节点都为空,那么它可以直接被删除。
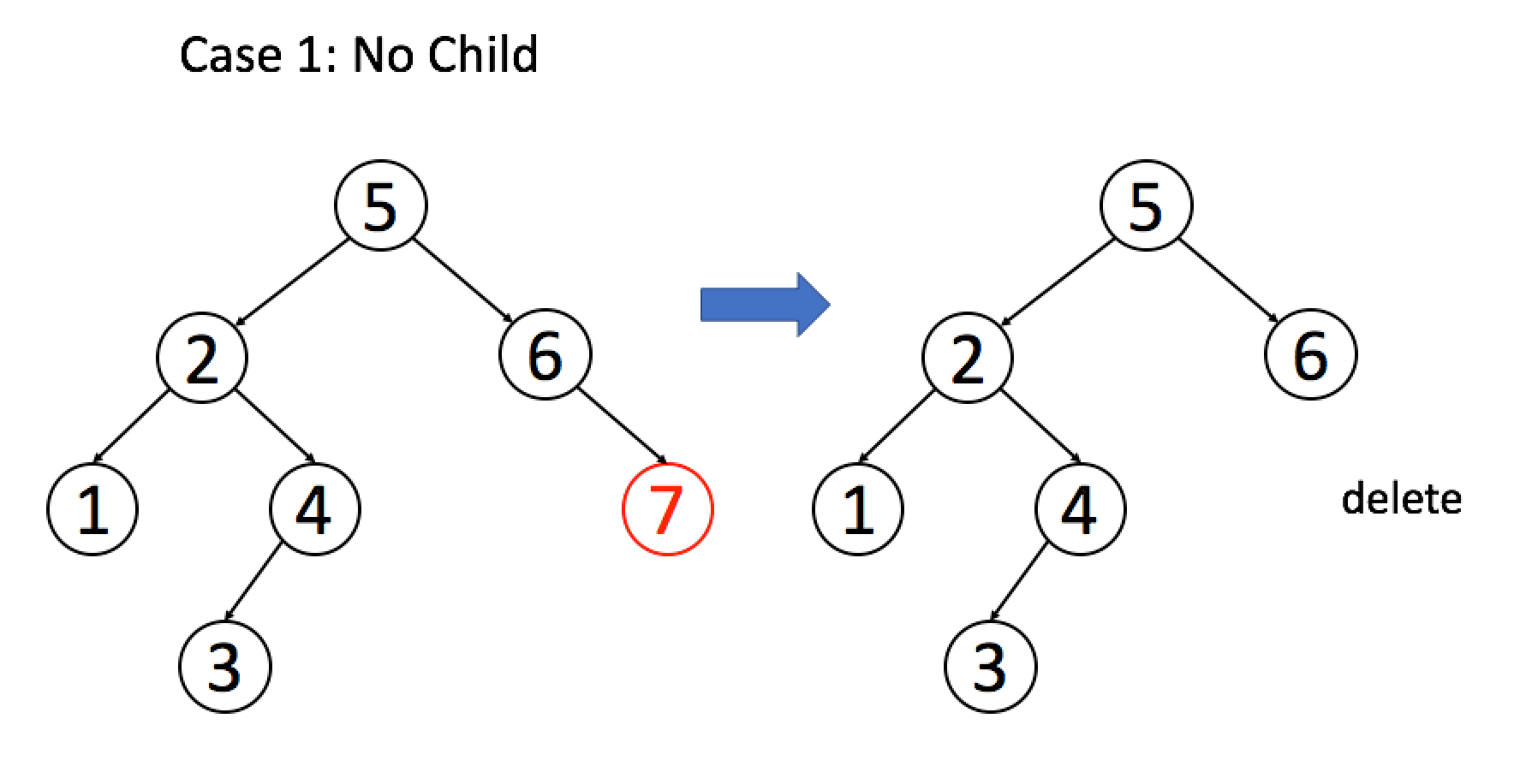
if (root.left == null && root.right == null)
return null;情况 2:A 只有一个非空子节点,那么它要让这个孩子接替自己的位置。
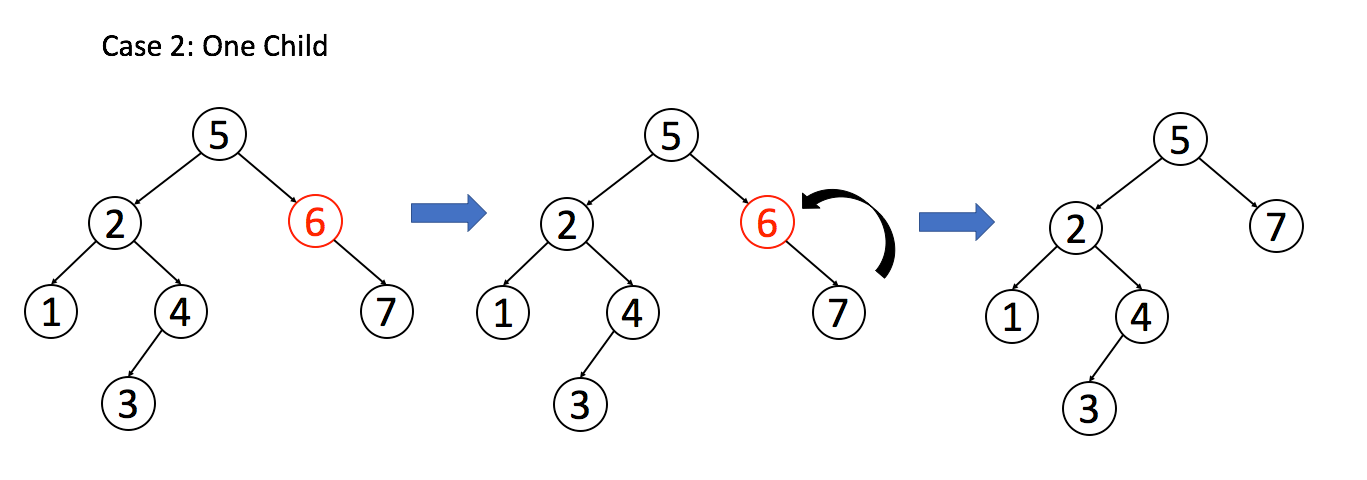
// 排除了情况 1 之后
if (root.left == null) return root.right;
if (root.right == null) return root.left;情况 3:A 有两个子节点,麻烦了,为了不破坏 BST 的性质,A 必须找到左子树中最大的那个节点,或者右子树中最小的那个节点来接替自己。我们以第二种方式讲解。
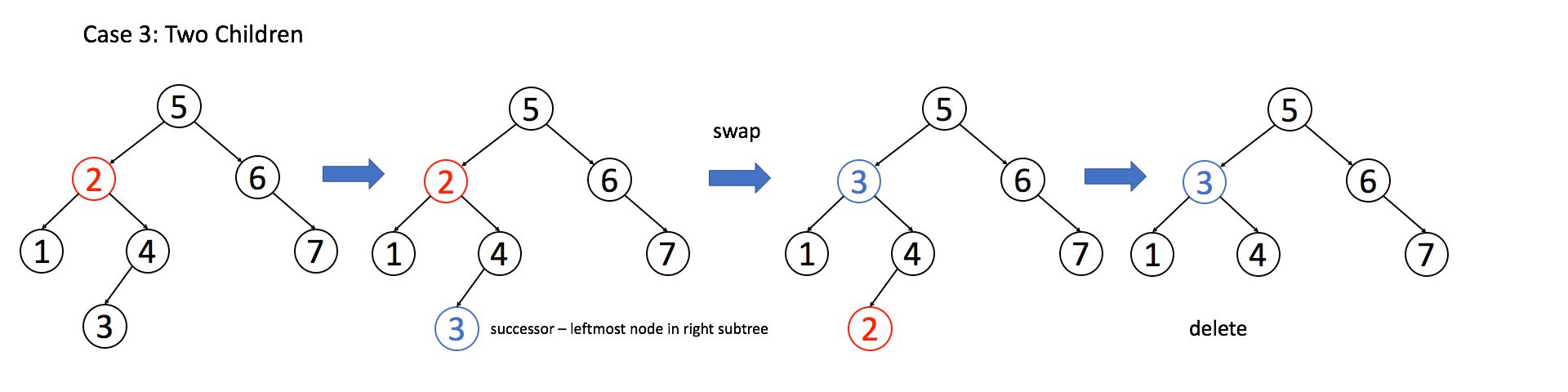
if (root.left != null && root.right != null) {
// 找到右子树的最小节点
TreeNode minNode = getMin(root.right);
// 把 root 改成 minNode
root.val = minNode.val;
// 转而去删除 minNode
root.right = deleteNode(root.right, minNode.val);
}三种情况分析完毕,填入框架,简化一下代码:
class Solution:
# 定义:在以 root 为根的 BST 中删除值为 key 的节点,返回完成删除后的根节点
def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
if root == None:
return None
if root.val == key:
# 这两个 if 把情况 1 和 2 都正确处理了
if root.left == None:
return root.right
if root.right == None:
return root.left
# 处理情况 3
# 获得右子树最小的节点
minNode = self.getMin(root.right)
# 删除右子树最小的节点
root.right = self.deleteNode(root.right, minNode.val)
# 用右子树最小的节点替换 root 节点
minNode.left = root.left
minNode.right = root.right
root = minNode
elif root.val > key:
root.left = self.deleteNode(root.left, key)
elif root.val < key:
root.right = self.deleteNode(root.right, key)
return root
def getMin(self, node: TreeNode) -> TreeNode:
# BST 最左边的就是最小的
while node.left != None:
node = node.left
return node算法可视化面板
这样,删除操作就完成了。注意一下,上述代码在处理情况 3 时通过一系列略微复杂的链表操作交换 root 和 minNode 两个节点:
// 处理情况 3
// 获得右子树最小的节点
TreeNode minNode = getMin(root.right);
// 删除右子树最小的节点
root.right = deleteNode(root.right, minNode.val);
// 用右子树最小的节点替换 root 节点
minNode.left = root.left;
minNode.right = root.right;
root = minNode;有的读者可能会疑惑,替换 root 节点为什么这么麻烦,直接改 val 字段不就行了?看起来还更简洁易懂:
// 处理情况 3
// 获得右子树最小的节点
TreeNode minNode = getMin(root.right);
// 删除右子树最小的节点
root.right = deleteNode(root.right, minNode.val);
// 用右子树最小的节点替换 root 节点
root.val = minNode.val;仅对于这道算法题来说是可以的,但这样操作并不完美,我们一般不会通过修改节点内部的值来交换节点。因为在实际应用中,BST 节点内部的数据域是用户自定义的,可以非常复杂,而 BST 作为数据结构(一个工具人),其操作应该和内部存储的数据域解耦,所以我们更倾向于使用指针操作来交换节点,根本没必要关心内部数据。
最后简单总结一下吧,通过这篇文章,我们总结出了如下几个技巧:
1、如果当前节点会对下面的子节点有整体影响,可以通过辅助函数增长参数列表,借助参数传递信息。
2、掌握 BST 的增删查改方法。
3、递归修改数据结构时,需要对递归调用的返回值进行接收,并返回修改后的节点。



