【练习】用「遍历」思维解题 I
一般来说,如果让你在二叉树的「树枝」上做文章,那么用遍历的思维模式解题是比较自然的想法。
257. 二叉树的所有路径
257. 二叉树的所有路径 | 力扣 | LeetCode | 🟢
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:

输入:root = [1,2,3,null,5] 输出:["1->2->5","1->3"]
示例 2:
输入:root = [1] 输出:["1"]
提示:
- 树中节点的数目在范围
[1, 100]内 -100 <= Node.val <= 100
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
你让我求所有根节点到叶子节点的路径,那我遍历一遍二叉树肯定可以搞定,遍历到叶子节点的时候想办法把路径生成出来就行了。
详细题解:
解法代码
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
# 遍历一遍二叉树就能出结果了
self.traverse(root)
return self.res
def __init__(self):
# 记录 traverse 函数递归时的路径
self.path = []
# 记录所有从根节点到叶子节点的路径
self.res = []
def traverse(self, root: TreeNode):
if root is None:
return
# root 是叶子节点
if root.left is None and root.right is None:
self.path.append(str(root.val))
# 将这条路径装入 res
self.res.append("->".join(self.path))
self.path.pop()
return
# 前序遍历位置
self.path.append(str(root.val))
# 递归遍历左右子树
self.traverse(root.left)
self.traverse(root.right)
# 后序遍历位置
self.path.pop()可视化
算法可视化面板
129. 求根节点到叶节点数字之和
129. 求根节点到叶节点数字之和 | 力扣 | LeetCode | 🟠
root ,树中每个节点都存放有一个 0 到 9 之间的数字。每条从根节点到叶节点的路径都代表一个数字:
- 例如,从根节点到叶节点的路径
1 -> 2 -> 3表示数字123。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1:

输入:root = [1,2,3] 输出:25 解释: 从根到叶子节点路径1->2代表数字12从根到叶子节点路径1->3代表数字13因此,数字总和 = 12 + 13 =25
示例 2:

输入:root = [4,9,0,5,1] 输出:1026 解释: 从根到叶子节点路径4->9->5代表数字 495 从根到叶子节点路径4->9->1代表数字 491 从根到叶子节点路径4->0代表数字 40 因此,数字总和 = 495 + 491 + 40 =1026
提示:
- 树中节点的数目在范围
[1, 1000]内 0 <= Node.val <= 9- 树的深度不超过
10
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
你想,让我获取所有路径数字之和,那我递归遍历一遍二叉树,沿路记录下来路径上的数字,到叶子节点的时候求和,不就完事了?
详细题解:
解法代码
class Solution:
def __init__(self):
self.path = ""
self.res = 0
def sumNumbers(self, root: TreeNode) -> int:
# 遍历一遍二叉树就能出结果
self.traverse(root)
return self.res
# 二叉树遍历函数
def traverse(self, root):
if root is None:
return
# 前序遍历位置,记录节点值
self.path += str(root.val)
if root.left is None and root.right is None:
# 到达叶子节点,累加路径和
self.res += int(self.path)
# 二叉树递归框架,遍历左右子树
self.traverse(root.left)
self.traverse(root.right)
# 后续遍历位置,撤销节点值
self.path = self.path[:-1]类似题目:
199. 二叉树的右视图
199. 二叉树的右视图 | 力扣 | LeetCode | 🟠
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:

输入: [1,2,3,null,5,null,4] 输出: [1,3,4]
示例 2:
输入: [1,null,3] 输出: [1,3]
示例 3:
输入: [] 输出: []
提示:
- 二叉树的节点个数的范围是
[0,100] -100 <= Node.val <= 100
基本思路
这题有两个思路:
1、用 BFS 层序遍历算法,每一层的最后一个节点就是二叉树的右侧视图。我们可以把 BFS 反过来,从右往左遍历每一行,进一步提升效率。
2、用 DFS 递归遍历算法,同样需要反过来,先递归 root.right 再递归 root.left,同时用 res 记录每一层的最右侧节点作为右侧视图。
详细题解:
解法代码
from collections import deque
class Solution:
# BFS 层序遍历解法
def rightSideView(self, root) -> list:
res = []
if root is None:
return res
# BFS 层序遍历,计算右侧视图
q = deque([root])
# while 循环控制从上向下一层层遍历
while q:
sz = len(q)
# 每一层头部就是最右侧的元素
last = q[0]
for i in range(sz):
cur = q.popleft()
# 控制每一层从右向左遍历
if cur.right:
q.append(cur.right)
if cur.left:
q.append(cur.left)
# 每一层的最后一个节点就是二叉树的右侧视图
res.append(last.val)
return res
# DFS 递归遍历解法
def rightSideView_DFS(self, root) -> list:
self.res = []
# 记录递归的层数
self.depth = 0
self.traverse(root)
return self.res
# 二叉树遍历函数
def traverse(self, root):
if root is None:
return
# 前序遍历位置
self.depth += 1
if len(self.res) < self.depth:
# 这一层还没有记录值
# 说明 root 就是右侧视图的第一个节点
self.res.append(root.val)
# 注意,这里反过来,先遍历右子树再遍历左子树
# 这样首先遍历的一定是右侧节点
self.traverse(root.right)
self.traverse(root.left)
# 后序遍历位置
self.depth -= 1
# 从左到右正常遍历
class Solution:
def __init__(self):
self.res = []
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
self.bfs(root)
return self.res
def bfs(self, root: Optional[TreeNode]):
if root is None:
return
q = [root]
while q:
sz = len(q)
self.res.append(q[-1].val)
for _ in range(sz):
cur = q.pop(0) # 移除并返回第一个元素
if cur.left:
q.append(cur.left)
if cur.right:
q.append(cur.right)可视化
算法可视化面板
类似题目:
988. 从叶结点开始的最小字符串
988. 从叶结点开始的最小字符串 | 力扣 | LeetCode | 🟠
给定一颗根结点为 root 的二叉树,树中的每一个结点都有一个 [0, 25] 范围内的值,分别代表字母 'a' 到 'z'。
返回 按字典序最小 的字符串,该字符串从这棵树的一个叶结点开始,到根结点结束。
注:字符串中任何较短的前缀在 字典序上 都是 较小 的:
- 例如,在字典序上
"ab"比"aba"要小。叶结点是指没有子结点的结点。
节点的叶节点是没有子节点的节点。
示例 1:

输入:root = [0,1,2,3,4,3,4] 输出:"dba"
示例 2:

输入:root = [25,1,3,1,3,0,2] 输出:"adz"
示例 3:

输入:root = [2,2,1,null,1,0,null,0] 输出:"abc"
提示:
- 给定树的结点数在
[1, 8500]范围内 0 <= Node.val <= 25
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
代码看起来虽然多,但思路非常简单:用 path 维护递归遍历的路径,到达叶子节点的时候判断字典序最小的路径。
不要忘了在叶子节点的时候也要正确维护 path 变量,而且要把 StringBuilder 中的字符串反转才是题目想要的答案。
详细题解:
解法代码
class Solution:
def smallestFromLeaf(self, root: TreeNode) -> str:
self.traverse(root)
return self.res
# 遍历过程中的路径
path = ""
res = None
# 二叉树遍历函数
def traverse(self, root):
if root is None:
return
if root.left is None and root.right is None:
# 找到叶子结点,比较字典序最小的路径
# 结果字符串是从叶子向根,所以需要反转
self.path = chr(ord('a') + root.val) + self.path
s = self.path
if self.res is None or self.res > s:
# 如果字典序更小,则更新 res
self.res = s
# 恢复,正确维护 path 中的元素
self.path = self.path[1:]
return
# 前序位置
self.path = chr(ord('a') + root.val) + self.path
self.traverse(root.left)
self.traverse(root.right)
# 后序位置
self.path = self.path[1:]可视化
算法可视化面板
1022. 从根到叶的二进制数之和
1022. 从根到叶的二进制数之和 | 力扣 | LeetCode | 🟢
给出一棵二叉树,其上每个结点的值都是 0 或 1 。每一条从根到叶的路径都代表一个从最高有效位开始的二进制数。
- 例如,如果路径为
0 -> 1 -> 1 -> 0 -> 1,那么它表示二进制数01101,也就是13。
对树上的每一片叶子,我们都要找出从根到该叶子的路径所表示的数字。
返回这些数字之和。题目数据保证答案是一个 32 位 整数。
示例 1:

输入:root = [1,0,1,0,1,0,1] 输出:22 解释:(100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22
示例 2:
输入:root = [0] 输出:0
提示:
- 树中的节点数在
[1, 1000]范围内 Node.val仅为0或1
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
用 path 变量维护每一条从根节点到叶子节点的路径形成的二进制数,到了叶子节点之后将这条路径的二进制数累加到 res 中即可。
详细题解:
解法代码
class Solution:
def sumRootToLeaf(self, root: TreeNode) -> int:
self.path = 0
self.res = 0
self.traverse(root)
return self.res
def traverse(self, root: TreeNode):
if root is None:
return
if root.left is None and root.right is None:
# 叶子节点
self.res += self.path << 1 | root.val
return
# 前序位置
self.path = self.path << 1 | root.val
self.traverse(root.left)
self.traverse(root.right)
# 后序位置
self.path = self.path >> 1可视化
算法可视化面板
1457. 二叉树中的伪回文路径
1457. 二叉树中的伪回文路径 | 力扣 | LeetCode | 🟠
给你一棵二叉树,每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「伪回文」的,当它满足:路径经过的所有节点值的排列中,存在一个回文序列。
请你返回从根到叶子节点的所有路径中 伪回文 路径的数目。
示例 1:

输入:root = [2,3,1,3,1,null,1]
输出:2
解释:上图为给定的二叉树。总共有 3 条从根到叶子的路径:红色路径 [2,3,3] ,绿色路径 [2,1,1] 和路径 [2,3,1] 。
在这些路径中,只有红色和绿色的路径是伪回文路径,因为红色路径 [2,3,3] 存在回文排列 [3,2,3] ,绿色路径 [2,1,1] 存在回文排列 [1,2,1] 。
示例 2:

输入:root = [2,1,1,1,3,null,null,null,null,null,1]
输出:1
解释:上图为给定二叉树。总共有 3 条从根到叶子的路径:绿色路径 [2,1,1] ,路径 [2,1,3,1] 和路径 [2,1] 。
这些路径中只有绿色路径是伪回文路径,因为 [2,1,1] 存在回文排列 [1,2,1] 。
示例 3:
输入:root = [9] 输出:1
提示:
- 给定二叉树的节点数目在范围
[1, 105]内 1 <= Node.val <= 9
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
遍历一遍二叉树就能得到每条路径上的数字,但这题的考点在于,如何判断一组数字是否存在一个回文串组合?
稍加思考不难想到:如果一组数字中,只有最多一个数字出现的次数为奇数,剩余数字的出现次数均为偶数,那么这组数字可以组成一个回文串。
题目说了 1 <= root.val <= 9,所以我们可以用一个大小为 10 的 count 数组做计数器来记录每条路径上的元素出现次数,到达叶子节点之后根据元素出现的次数判断是否可以构成回文串。
当然,我们也可以用更巧妙的位运算来实现上述逻辑:
1、首先用到异或运算的特性,1 ^ 1 = 0, 0 ^ 0 = 0, 1 ^ 0 = 1。
2、其次用到 n & (n - 1) 去除二进制最后一个 1 的技巧,详见 东哥教你几招常用的位运算技巧。
我同时实现了这两种方法,供你参考。
详细题解:
解法代码
class Solution:
def __init__(self):
self.count = [0] * 10
self.res = 0
def pseudoPalindromicPaths(self, root: TreeNode) -> int:
self.traverse(root)
return self.res
# 二叉树遍历函数
def traverse(self, root: TreeNode):
if root is None:
return
if root.left is None and root.right is None:
# 遇到叶子节点,判断路径是否是伪回文串
self.count[root.val] += 1
# 如果路径上出现奇数次的数字个数大于 1,
# 则不可能组成回文串,反之则可以组成回文串
odd = 0
for n in self.count:
if n % 2 == 1:
odd += 1
if odd <= 1:
self.res += 1
self.count[root.val] -= 1
return
self.count[root.val] += 1
# 二叉树遍历框架
self.traverse(root.left)
self.traverse(root.right)
self.count[root.val] -= 1
# 用位运算代替数组计数,进一步提升效率
class Solution2:
def __init__(self):
self.count = 0
self.res = 0
def pseudoPalindromicPaths(self, root: TreeNode) -> int:
self.traverse(root)
return self.res
# 二叉树遍历函数
def traverse(self, root: TreeNode):
if root is None:
return
if root.left is None and root.right is None:
# 遇到叶子节点,判断路径是否是伪回文串
self.count ^= (1 << root.val)
# 判断二进制中只有一位 1,原理见 https://labuladong.online/algo/frequency-interview/bitwise-operation/
if (self.count & (self.count - 1)) == 0:
self.res += 1
self.count ^= (1 << root.val)
return
self.count ^= (1 << root.val)
# 二叉树遍历框架
self.traverse(root.left)
self.traverse(root.right)
self.count ^= (1 << root.val)可视化
算法可视化面板
404. 左叶子之和
404. 左叶子之和 | 力扣 | LeetCode | 🟢
给定二叉树的根节点 root ,返回所有左叶子之和。
示例 1:

输入: root = [3,9,20,null,null,15,7] 输出: 24 解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
示例 2:
输入: root = [1] 输出: 0
提示:
- 节点数在
[1, 1000]范围内 -1000 <= Node.val <= 1000
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
无非就是遍历一遍二叉树,然后找到那些左叶子节点,累加它们的值罢了。
详细题解:
解法代码
class Solution:
def __init__(self):
# 记录左叶子之和
self.sum = 0
def sumOfLeftLeaves(self, root: TreeNode) -> int:
self.traverse(root)
return self.sum
# 二叉树遍历函数
def traverse(self, root: TreeNode):
if root is None:
return
if (root.left is not None and
root.left.left is None and root.left.right is None):
# 找到左侧的叶子节点,记录累加值
self.sum += root.left.val
# 递归框架
self.traverse(root.left)
self.traverse(root.right)可视化
算法可视化面板
623. 在二叉树中增加一行
623. 在二叉树中增加一行 | 力扣 | LeetCode | 🟠
给定一个二叉树的根 root 和两个整数 val 和 depth ,在给定的深度 depth 处添加一个值为 val 的节点行。
注意,根节点 root 位于深度 1 。
加法规则如下:
- 给定整数
depth,对于深度为depth - 1的每个非空树节点cur,创建两个值为val的树节点作为cur的左子树根和右子树根。 cur原来的左子树应该是新的左子树根的左子树。cur原来的右子树应该是新的右子树根的右子树。- 如果
depth == 1意味着depth - 1根本没有深度,那么创建一个树节点,值val作为整个原始树的新根,而原始树就是新根的左子树。
示例 1:

输入: root = [4,2,6,3,1,5], val = 1, depth = 2 输出: [4,1,1,2,null,null,6,3,1,5]
示例 2:

输入: root = [4,2,null,3,1], val = 1, depth = 3 输出: [4,2,null,1,1,3,null,null,1]
提示:
- 节点数在
[1, 104]范围内 - 树的深度在
[1, 104]范围内 -100 <= Node.val <= 100-105 <= val <= 1051 <= depth <= the depth of tree + 1
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
用 traverse 函数遍历到对应行,进行插入即可。
详细题解:
解法代码
class Solution:
def __init__(self):
self.targetVal = 0
self.targetDepth = 0
def addOneRow(self, root: TreeNode, val: int, depth: int) -> TreeNode:
self.targetVal = val
self.targetDepth = depth
# 插入到第一行的话特殊对待一下
if self.targetDepth == 1:
newRoot = TreeNode(self.targetVal)
newRoot.left = root
return newRoot
# 遍历二叉树,走到对应行进行插入
self.traverse(root, 1)
return root
def traverse(self, root: TreeNode, curDepth: int):
if root is None:
return
# 前序遍历
if curDepth == self.targetDepth - 1:
# 进行插入
newLeft = TreeNode(self.targetVal)
newRight = TreeNode(self.targetVal)
newLeft.left = root.left
newRight.right = root.right
root.left = newLeft
root.right = newRight
# Recursively traverse the left and right subtree
self.traverse(root.left, curDepth + 1)
self.traverse(root.right, curDepth + 1)
# 后序遍历
# Note: The original Java code does not have any action in the post-order position,
# but we keep the comment for consistency.可视化
算法可视化面板
971. 翻转二叉树以匹配先序遍历
971. 翻转二叉树以匹配先序遍历 | 力扣 | LeetCode | 🟠
给你一棵二叉树的根节点 root ,树中有 n 个节点,每个节点都有一个不同于其他节点且处于 1 到 n 之间的值。
另给你一个由 n 个值组成的行程序列 voyage ,表示 预期 的二叉树 先序遍历 结果。
通过交换节点的左右子树,可以 翻转 该二叉树中的任意节点。例,翻转节点 1 的效果如下:

请翻转 最少 的树中节点,使二叉树的 先序遍历 与预期的遍历行程 voyage 相匹配 。
如果可以,则返回 翻转的 所有节点的值的列表。你可以按任何顺序返回答案。如果不能,则返回列表 [-1]。
示例 1:

输入:root = [1,2], voyage = [2,1] 输出:[-1] 解释:翻转节点无法令先序遍历匹配预期行程。
示例 2:

输入:root = [1,2,3], voyage = [1,3,2] 输出:[1] 解释:交换节点 2 和 3 来翻转节点 1 ,先序遍历可以匹配预期行程。
示例 3:

输入:root = [1,2,3], voyage = [1,2,3] 输出:[] 解释:先序遍历已经匹配预期行程,所以不需要翻转节点。
提示:
- 树中的节点数目为
n n == voyage.length1 <= n <= 1001 <= Node.val, voyage[i] <= n- 树中的所有值 互不相同
voyage中的所有值 互不相同
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
用 traverse 函数遍历整棵二叉树,对比前序遍历结果,如果节点的值对不上,就无解;如果子树对不上 voyage,就尝试翻转子树。
详细题解:
解法代码
class Solution:
def flipMatchVoyage(self, root: TreeNode, voyage: List[int]) -> List[int]:
self.res = []
self.i = 0
self.can_flip = True
def dfs(node):
# 遍历的过程中尝试进行反转
if not node or not self.can_flip:
return True
if node.val != voyage[self.i]:
# 节点的 val 对不上,必然无解
self.can_flip = False
return False
self.i += 1
# Only flip if there's a left child and the next value in voyage doesn't match the left child's value
if node.left and node.left.val != voyage[self.i]:
# 前序遍历结果不对,尝试翻转左右子树
self.res.append(node.val)
node.left, node.right = node.right, node.left
# 记录翻转节点
# Note: This comment was not in the original Java code, but added to match the pattern of comments.
# If this was not intended, it can be removed.
return dfs(node.left) and dfs(node.right)
if dfs(root):
return self.res
else:
return [-1]可视化
算法可视化面板
987. 二叉树的垂序遍历
987. 二叉树的垂序遍历 | 力扣 | LeetCode | 🔴
给你二叉树的根结点 root ,请你设计算法计算二叉树的 垂序遍历 序列。
对位于 (row, col) 的每个结点而言,其左右子结点分别位于 (row + 1, col - 1) 和 (row + 1, col + 1) 。树的根结点位于 (0, 0) 。
二叉树的 垂序遍历 从最左边的列开始直到最右边的列结束,按列索引每一列上的所有结点,形成一个按出现位置从上到下排序的有序列表。如果同行同列上有多个结点,则按结点的值从小到大进行排序。
返回二叉树的 垂序遍历 序列。
示例 1:

输入:root = [3,9,20,null,null,15,7] 输出:[[9],[3,15],[20],[7]] 解释: 列 -1 :只有结点 9 在此列中。 列 0 :只有结点 3 和 15 在此列中,按从上到下顺序。 列 1 :只有结点 20 在此列中。 列 2 :只有结点 7 在此列中。
示例 2:

输入:root = [1,2,3,4,5,6,7]
输出:[[4],[2],[1,5,6],[3],[7]]
解释:
列 -2 :只有结点 4 在此列中。
列 -1 :只有结点 2 在此列中。
列 0 :结点 1 、5 和 6 都在此列中。
1 在上面,所以它出现在前面。
5 和 6 位置都是 (2, 0) ,所以按值从小到大排序,5 在 6 的前面。
列 1 :只有结点 3 在此列中。
列 2 :只有结点 7 在此列中。
示例 3:

输入:root = [1,2,3,4,6,5,7] 输出:[[4],[2],[1,5,6],[3],[7]] 解释: 这个示例实际上与示例 2 完全相同,只是结点 5 和 6 在树中的位置发生了交换。 因为 5 和 6 的位置仍然相同,所以答案保持不变,仍然按值从小到大排序。
提示:
- 树中结点数目总数在范围
[1, 1000]内 0 <= Node.val <= 1000
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
看这题的难度是困难,但你别被吓住了,我们从简单的开始,如果以整棵树的根节点为坐标 (0, 0),你如何打印出其他节点的坐标?
很简单,写出如下代码遍历一遍二叉树即可:
void traverse(TreeNode root, int row, int col) {
if (root == null) {
return;
}
print(row, col);
traverse(root.left, row + 1, col - 1);
traverse(root.right, row + 1, col + 1);
}然后就简单了,把这些坐标收集起来,依据题目要求进行排序,组装成题目要求的返回数据格式即可。
详细题解:
解法代码
class Solution:
# 记录每个节点和对应的坐标 (row, col)
class Triple:
def __init__(self, node, row, col):
self.node = node
self.row = row
self.col = col
def verticalTraversal(self, root: TreeNode) -> List[List[int]]:
# 遍历二叉树,并且为所有节点生成对应的坐标
self.traverse(root, 0, 0)
# 根据题意,根据坐标值对所有节点进行排序:
# 按照 col 从小到大排序,col 相同的话按 row 从小到大排序,
# 如果 col 和 row 都相同,按照 node.val 从小到大排序。
self.nodes.sort(key=lambda x: (x.col, x.row, x.node.val))
# 将排好序的节点组装成题目要求的返回格式
res = collections.deque()
# 记录上一列编号,初始化一个特殊值
preCol = float('-inf')
for cur in self.nodes:
if cur.col != preCol:
# 开始记录新的一列
res.append(collections.deque())
preCol = cur.col
res[-1].append(cur.node.val)
return [list(col) for col in res]
def __init__(self):
self.nodes = []
# 二叉树遍历函数,记录所有节点对应的坐标
def traverse(self, root: TreeNode, row: int, col: int):
if root is None:
return
# 记录坐标
self.nodes.append(self.Triple(root, row, col))
# 二叉树遍历框架
self.traverse(root.left, row + 1, col - 1)
self.traverse(root.right, row + 1, col + 1)类似题目:
993. 二叉树的堂兄弟节点
993. 二叉树的堂兄弟节点 | 力扣 | LeetCode | 🟢
在二叉树中,根节点位于深度 0 处,每个深度为 k 的节点的子节点位于深度 k+1 处。
如果二叉树的两个节点深度相同,但 父节点不同 ,则它们是一对堂兄弟节点。
我们给出了具有唯一值的二叉树的根节点 root ,以及树中两个不同节点的值 x 和 y 。
只有与值 x 和 y 对应的节点是堂兄弟节点时,才返回 true 。否则,返回 false。
示例 1:
输入:root = [1,2,3,4], x = 4, y = 3 输出:false
示例 2:
输入:root = [1,2,3,null,4,null,5], x = 5, y = 4 输出:true
示例 3:

输入:root = [1,2,3,null,4], x = 2, y = 3 输出:false
提示:
- 二叉树的节点数介于
2到100之间。 - 每个节点的值都是唯一的、范围为
1到100的整数。
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
遍历找到 x,y 的深度和父节点,对比即可。
详细题解:
解法代码
class Solution:
def __init__(self):
self.parentX = None
self.parentY = None
self.depthX = 0
self.depthY = 0
self.x = 0
self.y = 0
def isCousins(self, root: TreeNode, x: int, y: int) -> bool:
self.x = x
self.y = y
self.traverse(root, 0, None)
if self.depthX == self.depthY and self.parentX != self.parentY:
# 判断 x,y 是否是表兄弟节点
return True
return False
def traverse(self, root: TreeNode, depth: int, parent: TreeNode) -> None:
if root is None:
return
if root.val == self.x:
# 找到 x,记录它的深度和父节点
self.parentX = parent
self.depthX = depth
if root.val == self.y:
# 找到 y,记录它的深度和父节点
self.parentY = parent
self.depthY = depth
self.traverse(root.left, depth + 1, root)
self.traverse(root.right, depth + 1, root)可视化
算法可视化面板
1315. 祖父节点值为偶数的节点和
1315. 祖父节点值为偶数的节点和 | 力扣 | LeetCode | 🟠
给你一棵二叉树,请你返回满足以下条件的所有节点的值之和:
- 该节点的祖父节点的值为偶数。(一个节点的祖父节点是指该节点的父节点的父节点。)
如果不存在祖父节点值为偶数的节点,那么返回 0 。
示例:

输入:root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5] 输出:18 解释:图中红色节点的祖父节点的值为偶数,蓝色节点为这些红色节点的祖父节点。
提示:
- 树中节点的数目在
1到10^4之间。 - 每个节点的值在
1到100之间。
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
很简单,遍历一遍二叉树,对于节点值为偶数的节点,累加它的孙子节点的值即可。
详细题解:
解法代码
class Solution:
def __init__(self):
self.sum = 0
def sumEvenGrandparent(self, root: TreeNode) -> int:
self.traverse(root)
return self.sum
# 二叉树的遍历函数
def traverse(self, root: TreeNode):
if root is None:
return
if root.val % 2 == 0:
# 累加左子树孙子节点的值
if root.left is not None:
if root.left.left is not None:
self.sum += root.left.left.val
if root.left.right is not None:
self.sum += root.left.right.val
# 累加右子树孙子节点的值
if root.right is not None:
if root.right.left is not None:
self.sum += root.right.left.val
if root.right.right is not None:
self.sum += root.right.right.val
# 二叉树的遍历框架
self.traverse(root.left)
self.traverse(root.right)可视化
算法可视化面板
1448. 统计二叉树中好节点的数目
1448. 统计二叉树中好节点的数目 | 力扣 | LeetCode | 🟠
给你一棵根为 root 的二叉树,请你返回二叉树中好节点的数目。
「好节点」X 定义为:从根到该节点 X 所经过的节点中,没有任何节点的值大于 X 的值。
示例 1:

输入:root = [3,1,4,3,null,1,5] 输出:4 解释:图中蓝色节点为好节点。 根节点 (3) 永远是个好节点。 节点 4 -> (3,4) 是路径中的最大值。 节点 5 -> (3,4,5) 是路径中的最大值。 节点 3 -> (3,1,3) 是路径中的最大值。
示例 2:

输入:root = [3,3,null,4,2] 输出:3 解释:节点 2 -> (3, 3, 2) 不是好节点,因为 "3" 比它大。
示例 3:
输入:root = [1] 输出:1 解释:根节点是好节点。
提示:
- 二叉树中节点数目范围是
[1, 10^5]。 - 每个节点权值的范围是
[-10^4, 10^4]。
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维,利用函数参数给子树传递信息。
函数参数 pathMax 记录从根节点到当前节点路径中的最大值,通过比较 root.val 和 pathMax 比较就可判断 root 节点是不是「好节点」。然后再把 pathMax 传递到子树中继续判断其他节点。
详细题解:
解法代码
class Solution:
def __init__(self):
self.count = 0
def goodNodes(self, root: TreeNode) -> int:
self.traverse(root, root.val)
return self.count
# 二叉树遍历函数,pathMax 参数记录从根节点到当前节点路径中的最大值
def traverse(self, root: TreeNode, pathMax: int):
if root is None:
return
if pathMax <= root.val:
# 找到一个「好节点」
self.count += 1
# 更新路径上的最大值
pathMax = max(pathMax, root.val)
self.traverse(root.left, pathMax)
self.traverse(root.right, pathMax)可视化
算法可视化面板
437. 路径总和 III
437. 路径总和 III | 力扣 | LeetCode | 🟠
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
示例 1:

输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 输出:3 解释:和等于 8 的路径有 3 条,如图所示。
示例 2:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:3
提示:
- 二叉树的节点个数的范围是
[0,1000] -109 <= Node.val <= 109-1000 <= targetSum <= 1000
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维模式。
这题的难度应该设置为困难,因为这题及要求你准确理解二叉树的前序后序遍历,还要熟悉前缀和技巧,把前缀和技巧用到二叉树上。
你可以先看前文 前缀和技巧,然后做一下 560. 和为K的子数组,应该能够理解这道题的思路了。
你把二叉树看做是数组,利用前后序遍历来维护前缀和,看下图就能理解解法中几个关键变量的关系了:
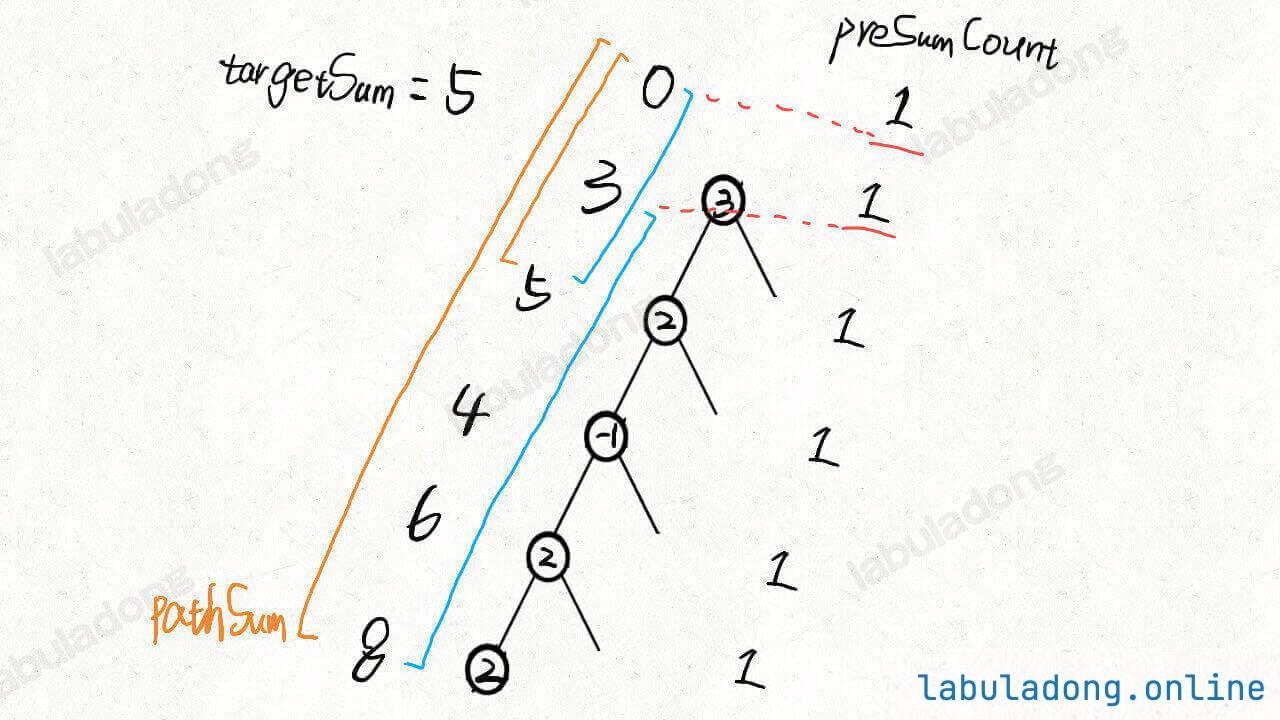
详细题解:
解法代码
class Solution:
# 记录前缀和
# 定义:从二叉树的根节点开始,路径和为 pathSum 的路径有 preSumCount.get(pathSum) 个
def __init__(self):
self.preSumCount = {}
self.path_sum = 0
self.target_sum = 0
self.res = 0
def pathSum(self, root: TreeNode, targetSum: int) -> int:
if root is None:
return 0
self.path_sum = 0
self.target_sum = targetSum
self.preSumCount[0] = 1
self.traverse(root)
return self.res
def traverse(self, root: TreeNode):
if root is None:
return
# 前序遍历位置
self.path_sum += root.val
# 从二叉树的根节点开始,路径和为 pathSum - targetSum 的路径条数
# 就是路径和为 targetSum 的路径条数
self.res += self.preSumCount.get(self.path_sum - self.target_sum, 0)
# 记录从二叉树的根节点开始,路径和为 pathSum 的路径条数
self.preSumCount[self.path_sum] = self.preSumCount.get(self.path_sum, 0) + 1
self.traverse(root.left)
self.traverse(root.right)
# 后序遍历位置
self.preSumCount[self.path_sum] = self.preSumCount.get(self.path_sum) - 1
self.path_sum -= root.val可视化
算法可视化面板
类似题目:
513. 找树左下角的值
513. 找树左下角的值 | 力扣 | LeetCode | 🟠
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
示例 1:

输入: root = [2,1,3] 输出: 1
示例 2:

输入: [1,2,3,4,null,5,6,null,null,7] 输出: 7
提示:
- 二叉树的节点个数的范围是
[1,104] -231 <= Node.val <= 231 - 1
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
二叉树递归框架代码是先递归左子树,后递归右子树,所以到最大深度时第一次遇到的节点就是左下角的节点。
当然,这题也可以用 BFS 层序遍历来做,留给你思考吧。
详细题解:
解法代码
class Solution:
def __init__(self):
# 记录二叉树的最大深度
self.maxDepth = 0
# 记录 traverse 递归遍历到的深度
self.depth = 0
self.res = None
def findBottomLeftValue(self, root: TreeNode) -> int:
self.traverse(root)
return self.res.val
def traverse(self, root: TreeNode):
if root is None:
return
# 前序遍历位置
self.depth += 1
if self.depth > self.maxDepth:
# 到最大深度时第一次遇到的节点就是左下角的节点
self.maxDepth = self.depth
self.res = root
self.traverse(root.left)
self.traverse(root.right)
# 后序遍历位置
self.depth -= 1可视化
算法可视化面板
类似题目:
1261. 在受污染的二叉树中查找元素
1261. 在受污染的二叉树中查找元素 | 力扣 | LeetCode | 🟠
给出一个满足下述规则的二叉树:
root.val == 0- 如果
treeNode.val == x且treeNode.left != null,那么treeNode.left.val == 2 * x + 1 - 如果
treeNode.val == x且treeNode.right != null,那么treeNode.right.val == 2 * x + 2
现在这个二叉树受到「污染」,所有的 treeNode.val 都变成了 -1。
请你先还原二叉树,然后实现 FindElements 类:
FindElements(TreeNode* root)用受污染的二叉树初始化对象,你需要先把它还原。bool find(int target)判断目标值target是否存在于还原后的二叉树中并返回结果。
示例 1:

输入: ["FindElements","find","find"] [[[-1,null,-1]],[1],[2]] 输出: [null,false,true] 解释: FindElements findElements = new FindElements([-1,null,-1]); findElements.find(1); // return False findElements.find(2); // return True
示例 2:

输入: ["FindElements","find","find","find"] [[[-1,-1,-1,-1,-1]],[1],[3],[5]] 输出: [null,true,true,false] 解释: FindElements findElements = new FindElements([-1,-1,-1,-1,-1]); findElements.find(1); // return True findElements.find(3); // return True findElements.find(5); // return False
示例 3:

输入: ["FindElements","find","find","find","find"] [[[-1,null,-1,-1,null,-1]],[2],[3],[4],[5]] 输出: [null,true,false,false,true] 解释: FindElements findElements = new FindElements([-1,null,-1,-1,null,-1]); findElements.find(2); // return True findElements.find(3); // return False findElements.find(4); // return False findElements.find(5); // return True
提示:
TreeNode.val == -1- 二叉树的高度不超过
20 - 节点的总数在
[1, 10^4]之间 - 调用
find()的总次数在[1, 10^4]之间 0 <= target <= 10^6
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
还原二叉树的时候只需要遍历所有节点,通过函数参数传递每个节点的值;由于节点的个数规模不算大,所以可以直接用一个 HashSet 缓存所有节点值,实现 find 函数的功能。
当然,题目给的这种二叉树节点的取值规律非常像用数组存储完全二叉树的场景,所以你应该可以通过 target 推算出来它在第几层的什么位置,不过我这里就不实现了,类似的题目你可以参考 1104. 二叉树寻路 和 662. 二叉树最大宽度。
详细题解:
解法代码
class FindElements:
# 帮助 find 函数快速判断
def __init__(self, root):
# 还原二叉树中的值
self.values = set()
self.traverse(root, 0)
# 二叉树遍历函数
def traverse(self, root, val):
if root is None:
return
root.val = val
self.values.add(val)
self.traverse(root.left, 2 * val + 1)
self.traverse(root.right, 2 * val + 2)
def find(self, target):
return target in self.values386. 字典序排数
386. 字典序排数 | 力扣 | LeetCode | 🟠
给你一个整数 n ,按字典序返回范围 [1, n] 内所有整数。
你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。
示例 1:
输入:n = 13 输出:[1,10,11,12,13,2,3,4,5,6,7,8,9]
示例 2:
输入:n = 2 输出:[1,2]
提示:
1 <= n <= 5 * 104
基本思路
这个题还挺有意思,要不是它把这道题放在 DFS 的题目分类里面,可能还不太好发现这是一个 DFS 的题目。
既然题目提示你这是个 DFS 的题目了,你心里那棵递归树出来没有?如果没有,建议去看看前文 二叉树视角学习递归思维。
它的递归树大概是这样生长的:
首先看 1 这个节点,1 可以生出二位数 10, 11, 12…
其中 10 又可以生出 100, 101, 102…,11 又可以生出 110, 111, 112…
这棵多叉树是不是就出来了?每个节点最多可以生出 10 个节点,这就是一个十叉树。
还是想不出来?看可视化面板。实际的解法代码需要以 1~9 分别作为根节点,画 9 棵多叉树,这里仅仅以 1 为根节点画递归树,方便你理解:
算法可视化面板
我们只需要以前序顺序遍历这棵多叉树,收集所有小于 n 的节点,就可以得到题目想要的答案。
详细题解:
解法代码
class Solution:
def __init__(self):
self.res = []
def lexicalOrder(self, n: int) -> List[int]:
# 总共有 9 棵多叉树,从 1 开始
for i in range(1, 10):
self.traverse(i, n)
return self.res
# 多叉树遍历框架,前序位置收集所有小于 n 的节点
def traverse(self, root: int, n: int) -> None:
if root > n:
return
self.res.append(root)
for child in range(root * 10, root * 10 + 10):
if child > n:
break
self.traverse(child, n)1104. 二叉树寻路
1104. 二叉树寻路 | 力扣 | LeetCode | 🟠
在一棵无限的二叉树上,每个节点都有两个子节点,树中的节点 逐行 依次按 “之” 字形进行标记。
如下图所示,在奇数行(即,第一行、第三行、第五行……)中,按从左到右的顺序进行标记;
而偶数行(即,第二行、第四行、第六行……)中,按从右到左的顺序进行标记。

给你树上某一个节点的标号 label,请你返回从根节点到该标号为 label 节点的路径,该路径是由途经的节点标号所组成的。
示例 1:
输入:label = 14 输出:[1,3,4,14]
示例 2:
输入:label = 26 输出:[1,2,6,10,26]
提示:
1 <= label <= 10^6
基本思路
如果你看过前文 二叉堆(优先级队列)原理及实现,就知道这种完全二叉树可以通过索引来模拟左右指针以及父节点指针。
具体来说,先假设全都是从左到右排列,没有之字形排列的这个条件:
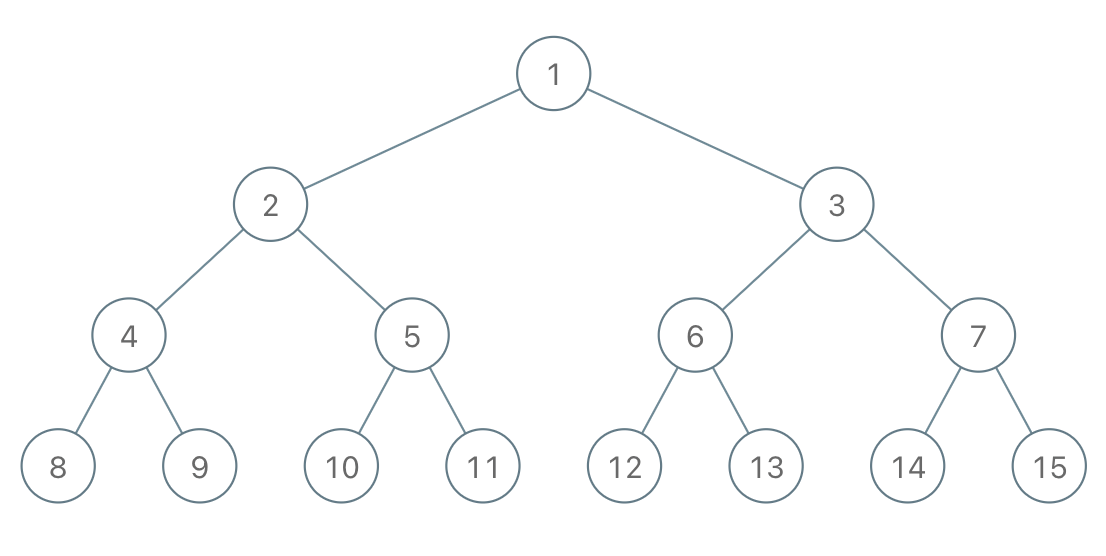
如果我想求到达某一个 label 节点的路径,那么我一直对 label 除以 2 就行了(忽略余数)。
你比如我想求到达 13 的路径,就是 13, 6, 3, 1,然后反转一下就行了。大致的代码逻辑如下:
ArrayList<Integer> path = new ArrayList<>();
while (label >= 1) {
path.add(label);
label = label / 2;
}
// 反转成从根节点到目标节点的路径
Collections.reverse(path);现在虽然是之字形排列,但稍加修改就可以适应这个变化:
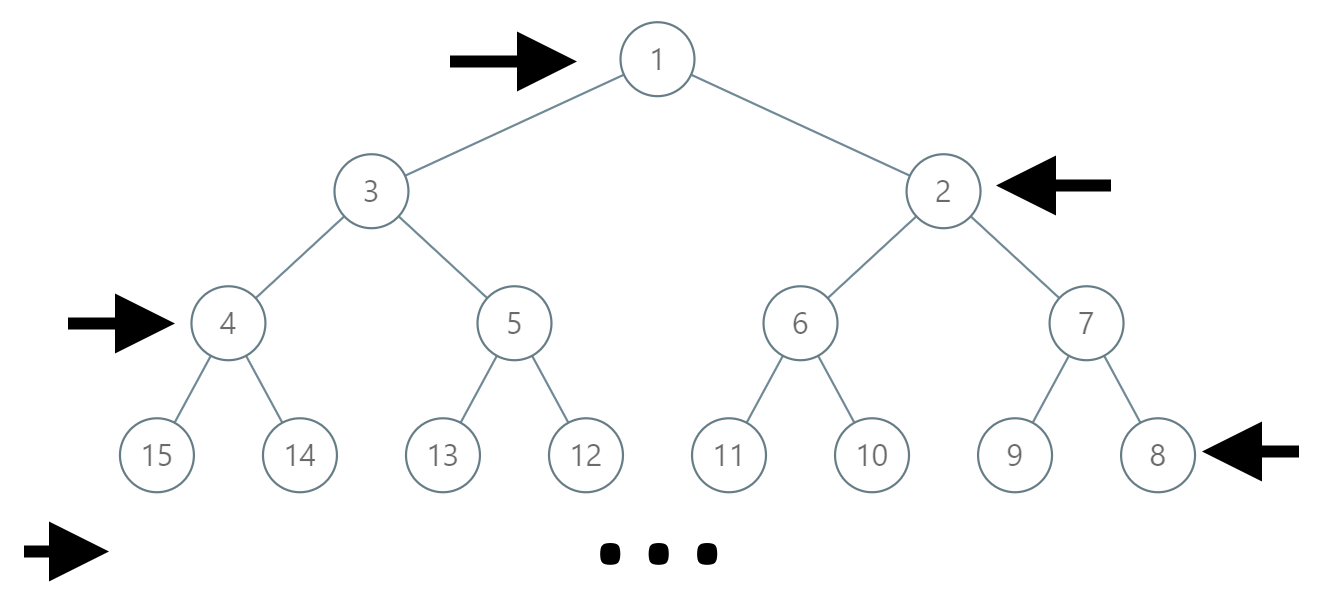
13 的父节点不是 6 了,而是 7 - (6 - 4) = 5。
这个 7 和 4 是哪里来的?就是 6 这一行的最小节点值和最大节点值,而对于完全二叉树,每一行的最大最小值可以通过计算 2 的指数算出来的。
理解了上述思路,就能看懂解法代码了。
详细题解:
解法代码
import math
from typing import List
class Solution:
def pathInZigZagTree(self, label: int) -> List[int]:
path = []
while label >= 1:
path.append(label)
label = label // 2
if label == 0:
break
depth = self.log(label)
range_ = self.getLevelRange(depth)
# 由于之字形分布,根据上层的节点取值范围,修正父节点
label = range_[1] - (label - range_[0])
# 反转成从根节点到目标节点的路径
path.reverse()
return path
# 获取第 n 层节点的取值范围
def getLevelRange(self, n: int) -> List[int]:
p = 2 ** n
return [p, 2 * p - 1]
def log(self, x: int) -> int:
if x == 0:
return 0
return int(math.log(x) / math.log(2))可视化
算法可视化面板
类似题目:
1145. 二叉树着色游戏
1145. 二叉树着色游戏 | 力扣 | LeetCode | 🟠
有两位极客玩家参与了一场「二叉树着色」的游戏。游戏中,给出二叉树的根节点 root,树上总共有 n 个节点,且 n 为奇数,其中每个节点上的值从 1 到 n 各不相同。
最开始时:
- 「一号」玩家从
[1, n]中取一个值x(1 <= x <= n); - 「二号」玩家也从
[1, n]中取一个值y(1 <= y <= n)且y != x。
「一号」玩家给值为 x 的节点染上红色,而「二号」玩家给值为 y 的节点染上蓝色。
之后两位玩家轮流进行操作,「一号」玩家先手。每一回合,玩家选择一个被他染过色的节点,将所选节点一个 未着色 的邻节点(即左右子节点、或父节点)进行染色(「一号」玩家染红色,「二号」玩家染蓝色)。
如果(且仅在此种情况下)当前玩家无法找到这样的节点来染色时,其回合就会被跳过。
若两个玩家都没有可以染色的节点时,游戏结束。着色节点最多的那位玩家获得胜利 ✌️。
现在,假设你是「二号」玩家,根据所给出的输入,假如存在一个 y 值可以确保你赢得这场游戏,则返回 true ;若无法获胜,就请返回 false 。
示例 1 :

输入:root = [1,2,3,4,5,6,7,8,9,10,11], n = 11, x = 3 输出:true 解释:第二个玩家可以选择值为 2 的节点。
示例 2 :
输入:root = [1,2,3], n = 3, x = 1 输出:false
提示:
- 树中节点数目为
n 1 <= x <= n <= 100n是奇数1 <= Node.val <= n- 树中所有值 互不相同
基本思路
这道题的关键是要观察规律,根据游戏规则,对方先选一个节点之后,你的最优策略就是紧贴着对方的那个节点选择,也就是说你应该选择节点 x 的左右子节点或者父节点。
做出以上三种选择,你可以占据二叉树的不同部分,如下图:
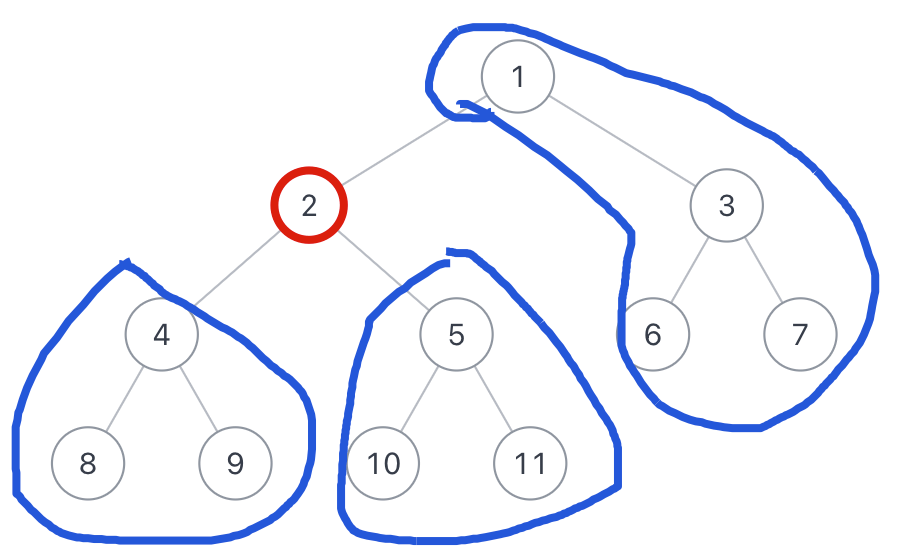
你如果想赢,必须占据超过 n / 2 的节点,也就是说,如果这三个蓝色区域中节点数最多的那个区域中的节点个数大于 n / 2,你能赢,否则你就输。
所以本题转化为计算二叉树节点个数的简单问题,具体看代码逻辑。
详细题解:
解法代码
class Solution:
def btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:
node = self.find(root, x)
left_count = self.count(node.left)
right_count = self.count(node.right)
other_count = n - 1 - left_count - right_count
return max(left_count, max(right_count, other_count)) > n // 2
# 定义:在以 root 为根的二叉树中搜索值为 x 的节点并返回
def find(self, root: TreeNode, x: int) -> TreeNode:
if root is None:
return None
if root.val == x:
return root
# 去左子树找
left = self.find(root.left, x)
if left is not None:
return left
# 左子树找不到的话去右子树找
return self.find(root.right, x)
# 定义:计算以 root 为根的二叉树的节点总数
def count(self, root: TreeNode) -> int:
if root is None:
return 0
return 1 + self.count(root.left) + self.count(root.right)可视化
算法可视化面板
2096. 从二叉树一个节点到另一个节点每一步的方向
2096. 从二叉树一个节点到另一个节点每一步的方向 | 力扣 | LeetCode | 🟠
给你一棵 二叉树 的根节点 root ,这棵二叉树总共有 n 个节点。每个节点的值为 1 到 n 中的一个整数,且互不相同。给你一个整数 startValue ,表示起点节点 s 的值,和另一个不同的整数 destValue ,表示终点节点 t 的值。
请找到从节点 s 到节点 t 的 最短路径 ,并以字符串的形式返回每一步的方向。每一步用 大写 字母 'L' ,'R' 和 'U' 分别表示一种方向:
'L'表示从一个节点前往它的 左孩子 节点。'R'表示从一个节点前往它的 右孩子 节点。'U'表示从一个节点前往它的 父 节点。
请你返回从 s 到 t 最短路径 每一步的方向。
示例 1:

输入:root = [5,1,2,3,null,6,4], startValue = 3, destValue = 6 输出:"UURL" 解释:最短路径为:3 → 1 → 5 → 2 → 6 。
示例 2:

输入:root = [2,1], startValue = 2, destValue = 1 输出:"L" 解释:最短路径为:2 → 1 。
提示:
- 树中节点数目为
n。 2 <= n <= 1051 <= Node.val <= n- 树中所有节点的值 互不相同 。
1 <= startValue, destValue <= nstartValue != destValue
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维模式。
这题的思路比较巧妙,主要分三步:
1、分别记录从根节点到 startValue 和 destValue 的路径 startPath 和 destPath。
2、然后去除 startPath 和 destPath 的公共前缀。
3、最后将 startPath 全部变成 U,把 startPath 和 destPath 接在一起,就是题目要求的路径了。
详细题解:
解法代码
class Solution:
def getDirections(self, root: TreeNode, startValue: int, destValue: int) -> str:
self.startValue = startValue
self.destValue = destValue
# 寻找走到 startValue 和 destValue 的方向路径
self.traverse(root)
# 去除两个方向路径的公共前缀
p = 0
m = len(self.startPath)
n = len(self.destPath)
while p < m and p < n and self.startPath[p] == self.destPath[p]:
p += 1
self.startPath = self.startPath[p:]
self.destPath = self.destPath[p:]
# 将走向 startValue 的方向路径全部变成 U
self.startPath = 'U' * len(self.startPath)
# 组合 startPath 和 destPath 就得到了答案
return self.startPath + self.destPath
def __init__(self):
self.path = ''
self.startPath = ''
self.destPath = ''
self.startValue = 0
self.destValue = 0
# 二叉树遍历函数
def traverse(self, root):
if root is None:
return
if root.val == self.startValue:
self.startPath = self.path
elif root.val == self.destValue:
self.destPath = self.path
# 二叉树遍历框架
self.path += 'L'
self.traverse(root.left)
self.path = self.path[:-1]
self.path += 'R'
self.traverse(root.right)
self.path = self.path[:-1]可视化
算法可视化面板
Tip
题目也可以让你在二叉树中寻找某棵子树,这种情况下会在递归函数中调用其他递归函数,时间复杂度会上升到平方级别,但也没有什么别的办法优化,只能通过遍历来对比子树。
572. 另一棵树的子树
572. 另一棵树的子树 | 力扣 | LeetCode | 🟢
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
示例 1:

输入:root = [3,4,5,1,2], subRoot = [4,1,2] 输出:true
示例 2:

输入:root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2] 输出:false
提示:
root树上的节点数量范围是[1, 2000]subRoot树上的节点数量范围是[1, 1000]-104 <= root.val <= 104-104 <= subRoot.val <= 104
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
遍历以 root 为根的这棵二叉树的所有节点,用 100. 相同的树 中的 isSame 函数判断以该节点为根的子树是否和以 subRoot 为根的那棵树相同。
详细题解:
class Solution:
def isSubtree(self, root: TreeNode, subRoot: TreeNode) -> bool:
if root is None:
return subRoot is None
# 判断以 root 为根的二叉树是否和 subRoot 相同
if self.isSameTree(root, subRoot):
return True
# 去左右子树中判断是否有和 subRoot 相同的子树
return self.isSubtree(root.left, subRoot) or self.isSubtree(root.right, subRoot)
def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
# 判断一对节点是否相同
if p is None and q is None:
return True
if p is None or q is None:
return False
if p.val != q.val:
return False
# 判断其他节点是否相同
return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)可视化
算法可视化面板
1367. 二叉树中的列表
1367. 二叉树中的链表 | 力扣 | LeetCode | 🟠
给你一棵以 root 为根的二叉树和一个 head 为第一个节点的链表。
如果在二叉树中,存在一条一直向下的路径,且每个点的数值恰好一一对应以 head 为首的链表中每个节点的值,那么请你返回 True ,否则返回 False 。
一直向下的路径的意思是:从树中某个节点开始,一直连续向下的路径。
示例 1:

输入:head = [4,2,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3] 输出:true 解释:树中蓝色的节点构成了与链表对应的子路径。
示例 2:

输入:head = [1,4,2,6], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3] 输出:true
示例 3:
输入:head = [1,4,2,6,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3] 输出:false 解释:二叉树中不存在一一对应链表的路径。
提示:
- 二叉树和链表中的每个节点的值都满足
1 <= node.val <= 100。 - 链表包含的节点数目在
1到100之间。 - 二叉树包含的节点数目在
1到2500之间。
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
本质上,isSubPath 就是在遍历二叉树的所有节点,对每个节点用 check 函数判断是否能够将链表嵌进去。
详细题解:
解法代码
class Solution:
def isSubPath(self, head: ListNode, root: TreeNode) -> bool:
# base case
if head is None:
return True
if root is None:
return False
# 当找到一个二叉树节点的值等于链表头结点时
if head.val == root.val:
# 判断是否能把链表嵌进去
if self.check(head, root):
return True
# 继续去遍历其他节点尝试嵌入链表
return self.isSubPath(head, root.left) or self.isSubPath(head, root.right)
# 检查是否能够将链表嵌入二叉树
def check(self, head: ListNode, root: TreeNode) -> bool:
if head is None:
return True
if root is None:
return False
if head.val == root.val:
# 在子树上嵌入子链表
return self.check(head.next, root.left) or self.check(head.next, root.right)
return False可视化
算法可视化面板
【练习】用「分解问题」思维解题 I
105. 从前序与中序遍历序列构造二叉树
105. 从前序与中序遍历序列构造二叉树 | 力扣 | LeetCode | 🟠
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1] 输出: [-1]
提示:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorder和inorder均 无重复 元素inorder均出现在preorderpreorder保证 为二叉树的前序遍历序列inorder保证 为二叉树的中序遍历序列
基本思路
构造二叉树,第一件事一定是找根节点,然后想办法构造左右子树。
二叉树的前序和中序遍历结果的特点如下:
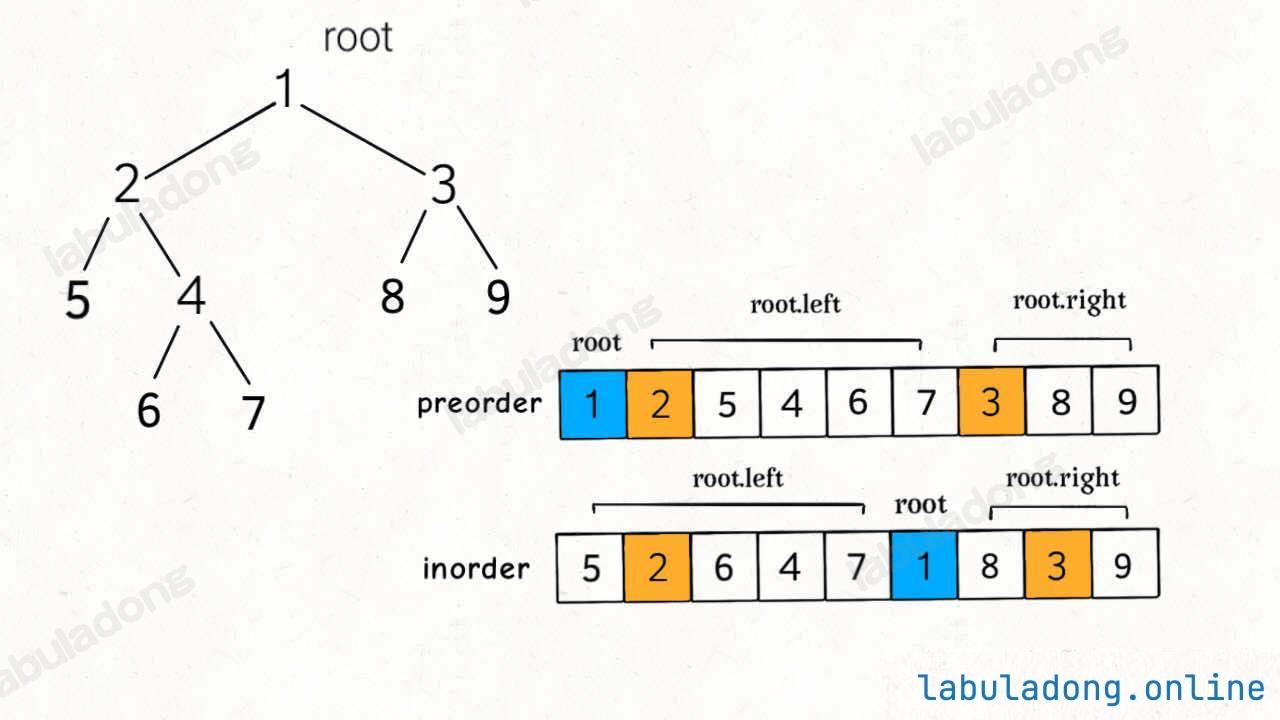
前序遍历结果第一个就是根节点的值,然后再根据中序遍历结果确定左右子树的节点。
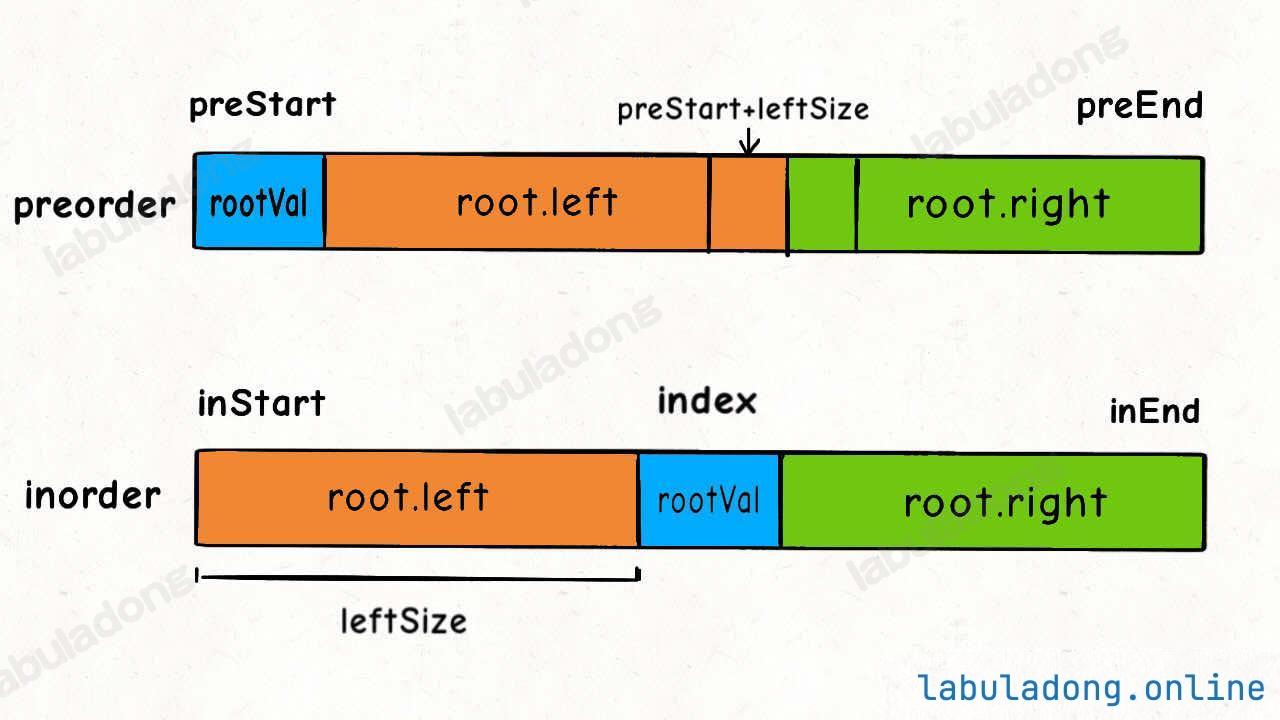
结合这个图看代码辅助理解。
详细题解:
解法代码
class Solution:
# 存储 inorder 中值到索引的映射
valToIndex = dict()
def buildTree(self, preorder, inorder):
for i in range(len(inorder)):
self.valToIndex[inorder[i]] = i
return self.build(preorder, 0, len(preorder) - 1,
inorder, 0, len(inorder) - 1)
# build 函数的定义:
# 若前序遍历数组为 preorder[preStart..preEnd],
# 中序遍历数组为 inorder[inStart..inEnd],
# 构造二叉树,返回该二叉树的根节点
def build(self, preorder, preStart, preEnd,
inorder, inStart, inEnd):
if preStart > preEnd:
return None
# root 节点对应的值就是前序遍历数组的第一个元素
rootVal = preorder[preStart]
# rootVal 在中序遍历数组中的索引
index = self.valToIndex[rootVal]
leftSize = index - inStart
# 先构造出当前根节点
root = TreeNode(rootVal)
# 递归构造左右子树
root.left = self.build(preorder, preStart + 1, preStart + leftSize,
inorder, inStart, index - 1)
root.right = self.build(preorder, preStart + leftSize + 1, preEnd,
inorder, index + 1, inEnd)
return root类似题目:
106. 从中序与后序遍历序列构造二叉树
106. 从中序与后序遍历序列构造二叉树 | 力扣 | LeetCode | 🟠
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:

输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] 输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1] 输出:[-1]
提示:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorder和postorder都由 不同 的值组成postorder中每一个值都在inorder中inorder保证是树的中序遍历postorder保证是树的后序遍历
基本思路
构造二叉树,第一件事一定是找根节点,然后想办法构造左右子树。
二叉树的后序和中序遍历结果的特点如下:
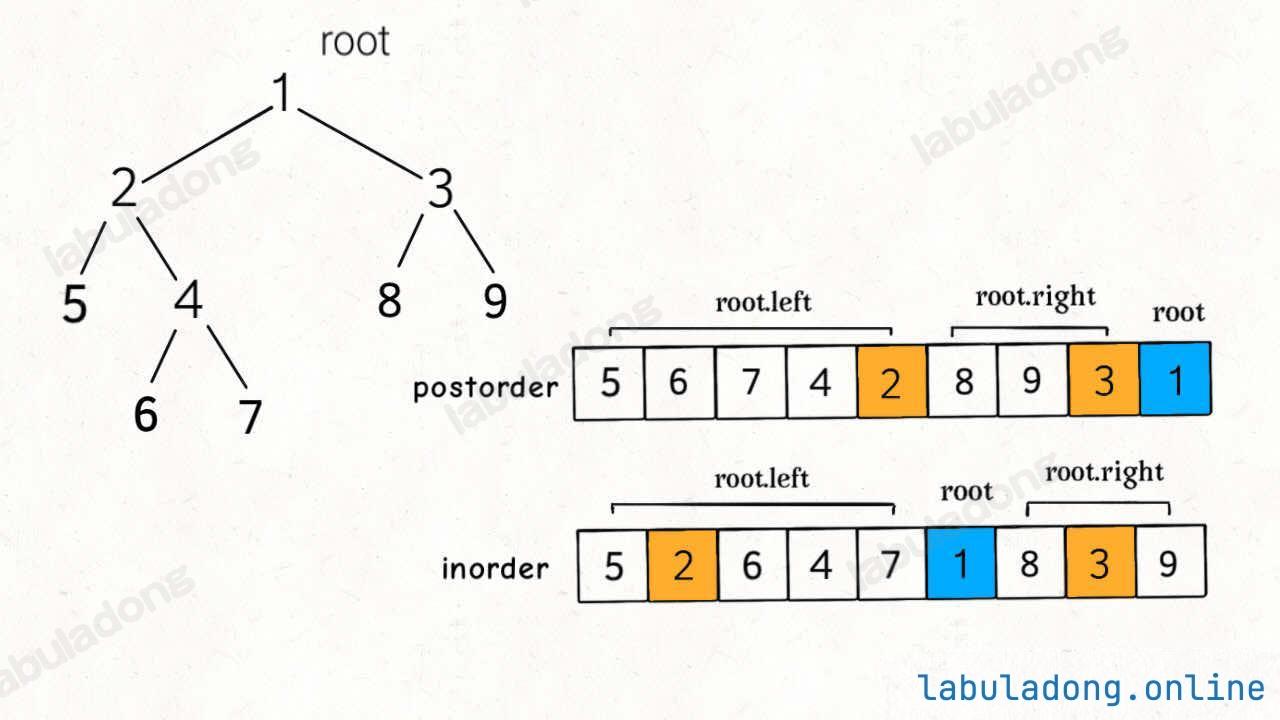
后序遍历结果最后一个就是根节点的值,然后再根据中序遍历结果确定左右子树的节点。
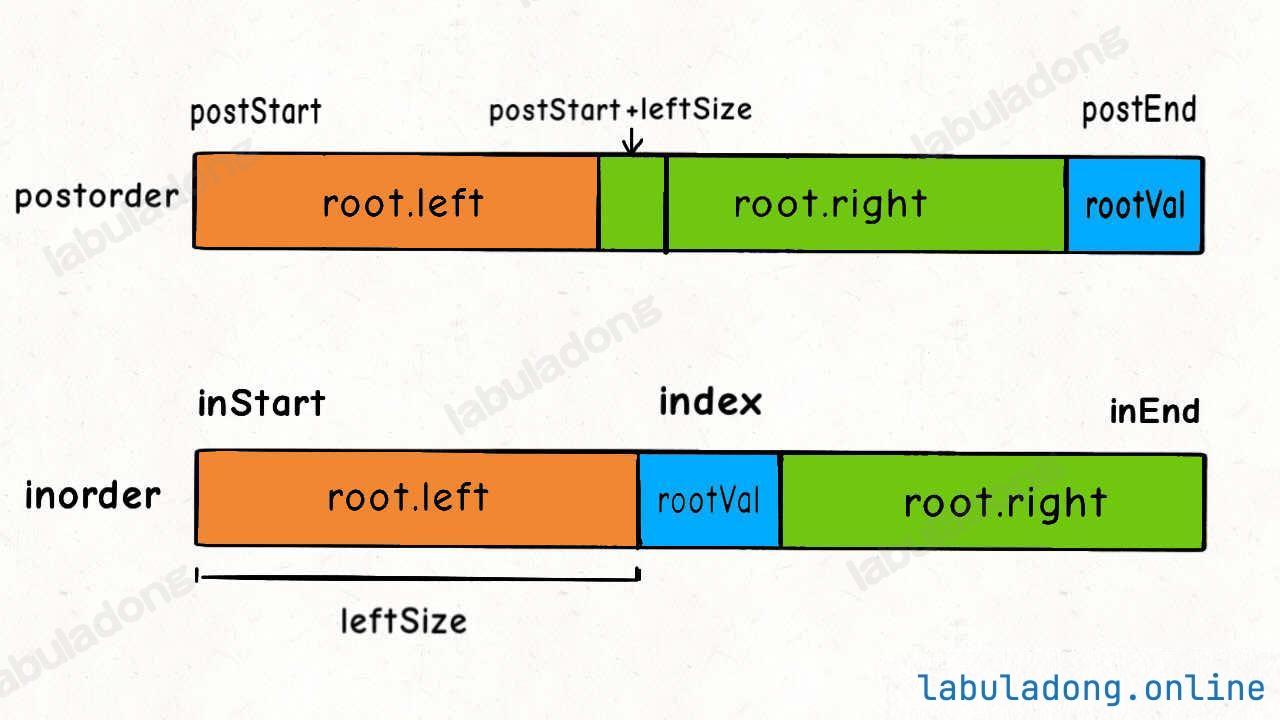
结合这个图看代码辅助理解。
详细题解:
解法代码
class Solution:
# 存储 inorder 中值到索引的映射
val_to_index = {}
def buildTree(self, inorder, postorder):
for i in range(len(inorder)):
self.val_to_index[inorder[i]] = i
return self.build(inorder, 0, len(inorder) - 1,
postorder, 0, len(postorder) - 1)
# 定义:中序遍历数组为 inorder[inStart..inEnd],
# 后序遍历数组为 postorder[postStart..postEnd],
# build 函数构造这个二叉树并返回该二叉树的根节点
def build(self, inorder, in_start, in_end,
postorder, post_start, post_end):
if in_start > in_end:
return None
# root 节点对应的值就是后序遍历数组的最后一个元素
root_val = postorder[post_end]
# rootVal 在中序遍历数组中的索引
index = self.val_to_index[root_val]
# 左子树的节点个数
left_size = index - in_start
root = TreeNode(root_val)
# 递归构造左右子树
root.left = self.build(inorder, in_start, index - 1,
postorder, post_start, post_start + left_size - 1)
root.right = self.build(inorder, index + 1, in_end,
postorder, post_start + left_size, post_end - 1)
return root可视化
算法可视化面板
类似题目:
889. 根据前序和后序遍历构造二叉树
889. 根据前序和后序遍历构造二叉树 | 力扣 | LeetCode | 🟠
给定两个整数数组,preorder 和 postorder ,其中 preorder 是一个具有 无重复 值的二叉树的前序遍历,postorder 是同一棵树的后序遍历,重构并返回二叉树。
如果存在多个答案,您可以返回其中 任何 一个。
示例 1:

输入:preorder = [1,2,4,5,3,6,7], postorder = [4,5,2,6,7,3,1] 输出:[1,2,3,4,5,6,7]
示例 2:
输入: preorder = [1], postorder = [1] 输出: [1]
提示:
1 <= preorder.length <= 301 <= preorder[i] <= preorder.lengthpreorder中所有值都 不同postorder.length == preorder.length1 <= postorder[i] <= postorder.lengthpostorder中所有值都 不同- 保证
preorder和postorder是同一棵二叉树的前序遍历和后序遍历
基本思路
做这道题之前,建议你先看一下 二叉树心法(构造篇),做一下 105. 从前序与中序遍历序列构造二叉树(中等) 和 106. 从中序与后序遍历序列构造二叉树(中等) 这两道题。
这道题让用后序遍历和前序遍历结果还原二叉树,和前两道题有一个本质的区别:
通过前序中序,或者后序中序遍历结果可以确定一棵原始二叉树,但是通过前序后序遍历结果无法确定原始二叉树。题目也说了,如果有多种结果,你可以返回任意一种。
为什么呢?我们说过,构建二叉树的套路很简单,先找到根节点,然后找到并递归构造左右子树即可。
前两道题,可以通过前序或者后序遍历结果找到根节点,然后根据中序遍历结果确定左右子树。
这道题,你可以确定根节点,但是无法确切的知道左右子树有哪些节点。
举个例子,下面这两棵树结构不同,但是它们的前序遍历和后序遍历结果是相同的:
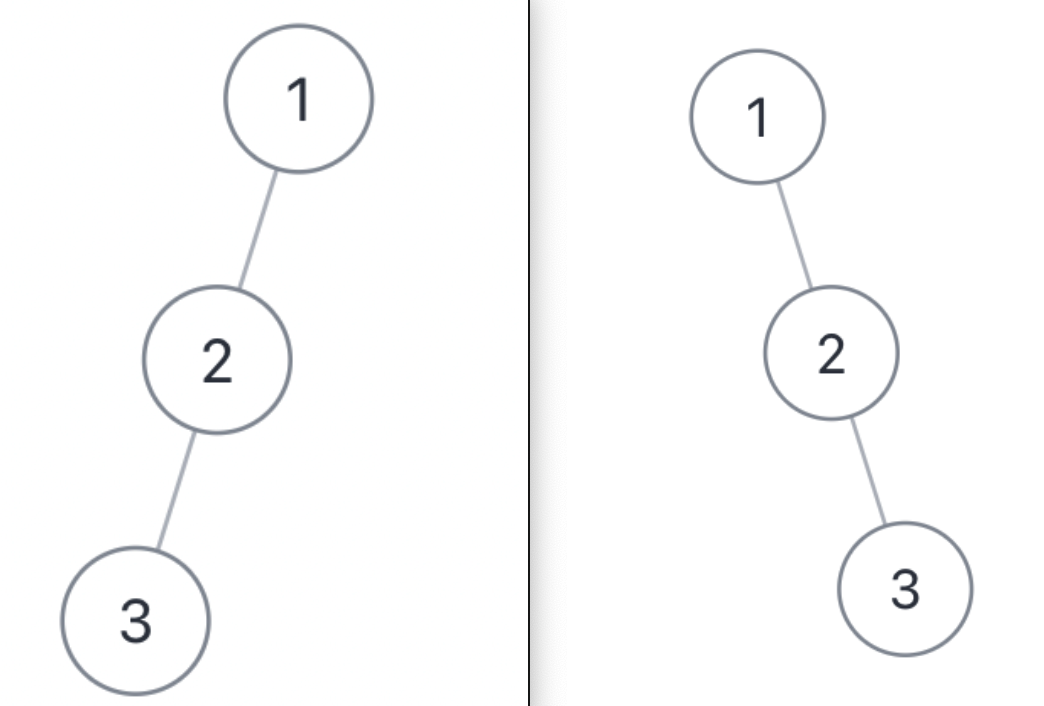
不过话说回来,用后序遍历和前序遍历结果还原二叉树,解法逻辑上和前两道题差别不大,也是通过控制左右子树的索引来构建:
1、首先把前序遍历结果的第一个元素或者后序遍历结果的最后一个元素确定为根节点的值。
2、然后把前序遍历结果的第二个元素作为左子树的根节点的值。
3、在后序遍历结果中寻找左子树根节点的值,从而确定了左子树的索引边界,进而确定右子树的索引边界,递归构造左右子树即可。
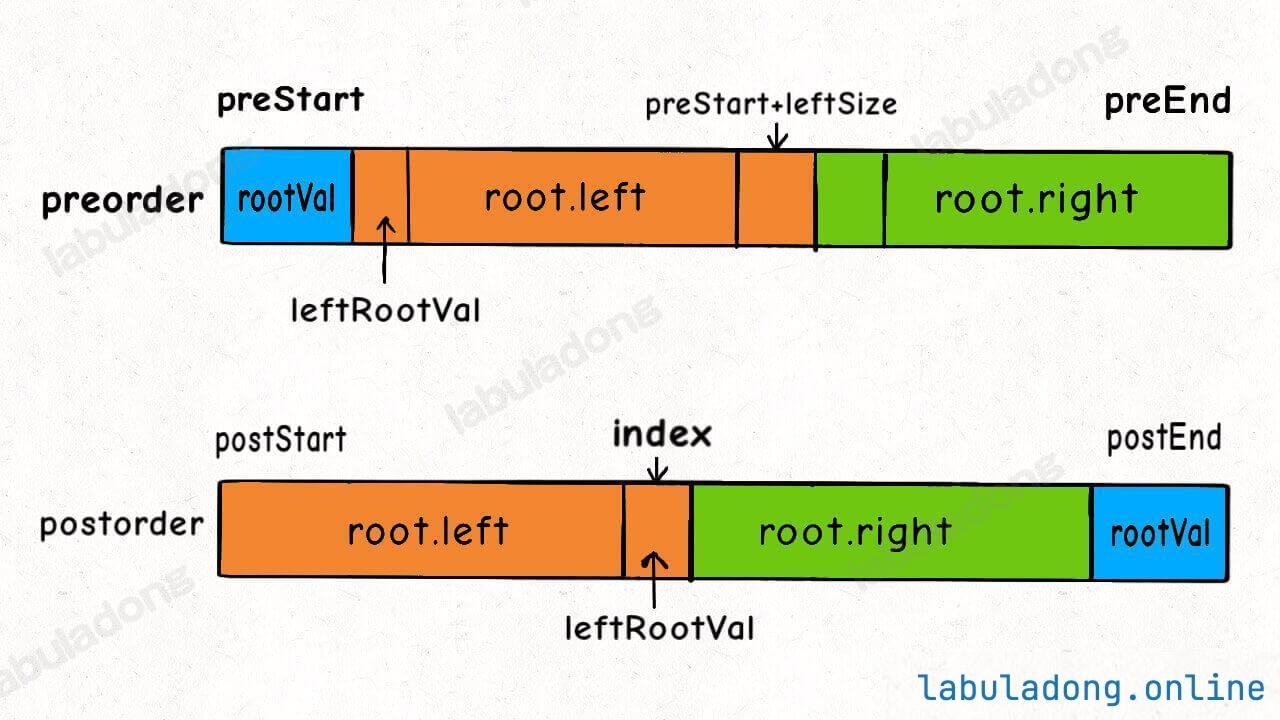
详细题解:
解法代码
class Solution:
# 存储 postorder 中值到索引的映射
valToIndex = dict()
def constructFromPrePost(self, preorder, postorder):
for i in range(len(postorder)):
self.valToIndex[postorder[i]] = i
return self.build(preorder, 0, len(preorder) - 1,
postorder, 0, len(postorder) - 1)
# 定义:根据 preorder[preStart..preEnd] 和 postorder[postStart..postEnd]
# 构建二叉树,并返回根节点。
def build(self, preorder, preStart, preEnd,
postorder, postStart, postEnd):
if preStart > preEnd:
return None
if preStart == preEnd:
return TreeNode(preorder[preStart])
# root 节点对应的值就是前序遍历数组的第一个元素
rootVal = preorder[preStart]
# root.left 的值是前序遍历第二个元素
# 通过前序和后序遍历构造二叉树的关键在于通过左子树的根节点
# 确定 preorder 和 postorder 中左右子树的元素区间
leftRootVal = preorder[preStart + 1]
# leftRootVal 在后序遍历数组中的索引
index = self.valToIndex[leftRootVal]
# 左子树的元素个数
leftSize = index - postStart + 1
# 先构造出当前根节点
root = TreeNode(rootVal)
# 递归构造左右子树
# 根据左子树的根节点索引和元素个数推导左右子树的索引边界
root.left = self.build(preorder, preStart + 1, preStart + leftSize,
postorder, postStart, index)
root.right = self.build(preorder, preStart + leftSize + 1, preEnd,
postorder, index + 1, postEnd - 1)
return root可视化
算法可视化面板
类似题目:
331. 验证二叉树的前序序列化
331. 验证二叉树的前序序列化 | 力扣 | LeetCode | 🟠
序列化二叉树的一种方法是使用 前序遍历 。当我们遇到一个非空节点时,我们可以记录下这个节点的值。如果它是一个空节点,我们可以使用一个标记值记录,例如 #。

例如,上面的二叉树可以被序列化为字符串 "9,3,4,#,#,1,#,#,2,#,6,#,#",其中 # 代表一个空节点。
给定一串以逗号分隔的序列,验证它是否是正确的二叉树的前序序列化。编写一个在不重构树的条件下的可行算法。
保证 每个以逗号分隔的字符或为一个整数或为一个表示 null 指针的 '#' 。
你可以认为输入格式总是有效的
- 例如它永远不会包含两个连续的逗号,比如
"1,,3"。
注意:不允许重建树。
示例 1:
输入: preorder ="9,3,4,#,#,1,#,#,2,#,6,#,#"输出:true
示例 2:
输入: preorder ="1,#"输出:false
示例 3:
输入: preorder ="9,#,#,1"输出:false
提示:
1 <= preorder.length <= 104preorder由以逗号“,”分隔的[0,100]范围内的整数和“#”组成
基本思路
首先,如果看过前文 手把手带你刷二叉树(序列化篇) 理解了前序遍历序列化和反序列化的原理,肯定可以通过改造反序列化函数 deserialize 来判断序列化的合法性。
另外还有一种更巧妙的解法,就是利用二叉树节点和边的关系。
每个非空的二叉树节点都会产生两条边,并消耗一条边;而每个空节点只会消耗一条边:
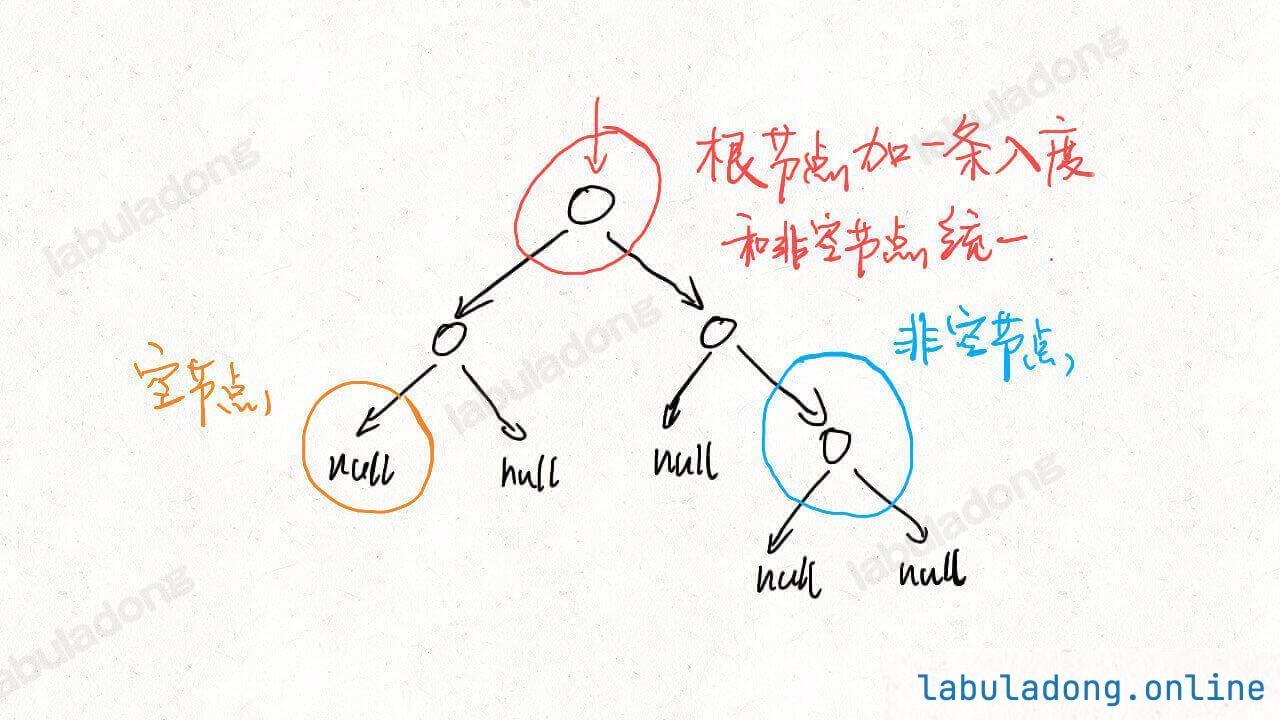
详细题解:
解法代码
class Solution:
def isValidSerialization(self, preorder: str) -> bool:
# 一条指向根节点的虚拟边
edge = 1
for node in preorder.split(","):
# 任何时候,边数都不能小于 0
if node == "#":
# 空指针消耗一条空闲边
edge -= 1
if edge < 0:
return False
else:
# 非空节点消耗一条空闲边,增加两条空闲边
edge -= 1
if edge < 0:
return False
edge += 2
# 最后不应该存在空闲边
return edge == 0
class Solution2:
def isValidSerialization(self, preorder: str) -> bool:
# 将字符串转化成列表
nodes = list(preorder.split(","))
return self.deserialize(nodes) and len(nodes) == 0
# 改造后的前序遍历反序列化函数
# 详细解析:https://labuladong.online/algo/data-structure/serialize-and-deserialize-binary-tree/
def deserialize(self, nodes) -> bool:
if not nodes:
return False
# ***** 前序遍历位置 *****
# 列表最左侧就是根节点
first = nodes.pop(0)
if first == "#":
return True
# *********************
return self.deserialize(nodes) and self.deserialize(nodes)可视化
算法可视化面板
894. 所有可能的满二叉树
894. 所有可能的真二叉树 | 力扣 | LeetCode | 🟠
给你一个整数 n ,请你找出所有可能含 n 个节点的 真二叉树 ,并以列表形式返回。答案中每棵树的每个节点都必须符合 Node.val == 0 。
答案的每个元素都是一棵真二叉树的根节点。你可以按 任意顺序 返回最终的真二叉树列表。
真二叉树 是一类二叉树,树中每个节点恰好有 0 或 2 个子节点。
示例 1:

输入:n = 7 输出:[[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]
示例 2:
输入:n = 3 输出:[[0,0,0]]
提示:
1 <= n <= 20
基本思路
注意:国外和国内关于完全二叉树、满二叉树的定义有区别,我在 二叉树基础知识 有介绍。不过这些文学词汇并不重要,重要的是算法思维,所以我们按照题目说的来就好。
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维。
如果你想生成一棵 n 个节点的满二叉树,首先要固定根节点,然后组装左右子树,根节点加上左右子树节点之和应该等于 n。
我们定义 helper 能够生成节点数为 n 的所有可能的二叉树,然后利用这个定义生成左右子树,然后通过子树组装出结果即可。
详细题解:
解法代码
class Solution:
# 备忘录,记录 n 个节点能够组合成的所有可能二叉树
memo = {}
def allPossibleFBT(self, n: int) -> List[TreeNode]:
if n % 2 == 0:
# 题目描述的满二叉树不可能是偶数个节点
return []
self.memo = {1: [TreeNode(0)]}
return self.build(n)
# 定义:输入一个 n,生成节点树为 n 的所有可能的满二叉树
def build(self, n: int) -> List[TreeNode]:
if n in self.memo:
# 避免冗余计算
return self.memo[n]
res = []
# base case
if n == 1:
return [TreeNode(0)]
# 递归生成所有符合条件的左右子树
for i in range(1, n, 2):
j = n - i - 1
# 利用函数定义,生成左右子树
leftSubTrees = self.build(i)
rightSubTrees = self.build(j)
# 左右子树的不同排列也能构成不同的二叉树
for left in leftSubTrees:
for right in rightSubTrees:
# 生成根节点
root = TreeNode(0)
# 组装出一种可能的二叉树形状
root.left = left
root.right = right
# 加入结果列表
res.append(root)
# 存入备忘录
self.memo[n] = res
return res可视化
算法可视化面板
998. 最大二叉树 II
998. 最大二叉树 II | 力扣 | LeetCode | 🟠
最大树 定义:一棵树,并满足:其中每个节点的值都大于其子树中的任何其他值。
给你最大树的根节点 root 和一个整数 val 。
就像 之前的问题 那样,给定的树是利用 Construct(a) 例程从列表 a(root = Construct(a))递归地构建的:
- 如果
a为空,返回null。 - 否则,令
a[i]作为a的最大元素。创建一个值为a[i]的根节点root。 root的左子树将被构建为Construct([a[0], a[1], ..., a[i - 1]])。root的右子树将被构建为Construct([a[i + 1], a[i + 2], ..., a[a.length - 1]])。- 返回
root。
请注意,题目没有直接给出 a ,只是给出一个根节点 root = Construct(a) 。
假设 b 是 a 的副本,并在末尾附加值 val。题目数据保证 b 中的值互不相同。
返回 Construct(b) 。
示例 1:


输入:root = [4,1,3,null,null,2], val = 5 输出:[5,4,null,1,3,null,null,2] 解释:a = [1,4,2,3], b = [1,4,2,3,5]
示例 2:

输入:root = [5,2,4,null,1], val = 3 输出:[5,2,4,null,1,null,3] 解释:a = [2,1,5,4], b = [2,1,5,4,3]
示例 3:

输入:root = [5,2,3,null,1], val = 4 输出:[5,2,4,null,1,3] 解释:a = [2,1,5,3], b = [2,1,5,3,4]
提示:
- 树中节点数目在范围
[1, 100]内 1 <= Node.val <= 100- 树中的所有值 互不相同
1 <= val <= 100
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维。
做这道题之前,你一定要去做一下 654. 最大二叉树 这道题,知道了构建最大二叉树的逻辑就很容易解决这道题了。
新增的 val 是添加在原始数组的最后的,根据构建最大二叉树的逻辑,正常来说最后的这个值一定是在右子树的,可以对右子树递归调用 insertIntoMaxTree 插入进去。
但是一种特殊情况是 val 比原始数组中的所有元素都大,那么根据构建最大二叉树的逻辑,原来的这棵树应该成为 val 节点的左子树。
详细题解:
解法代码
class Solution:
def insertIntoMaxTree(self, root: TreeNode, val: int) -> TreeNode:
if root is None:
return TreeNode(val)
if root.val < val:
# 如果 val 是整棵树最大的,那么原来的这棵树应该是 val 节点的左子树,
# 因为 val 节点是接在原始数组 a 的最后一个元素
temp = root
root = TreeNode(val)
root.left = temp
else:
# 如果 val 不是最大的,那么就应该在右子树上,
# 因为 val 节点是接在原始数组 a 的最后一个元素
root.right = self.insertIntoMaxTree(root.right, val)
return root可视化
算法可视化面板
1110. 删点成林
1110. 删点成林 | 力扣 | LeetCode | 🟠
给出二叉树的根节点 root,树上每个节点都有一个不同的值。
如果节点值在 to_delete 中出现,我们就把该节点从树上删去,最后得到一个森林(一些不相交的树构成的集合)。
返回森林中的每棵树。你可以按任意顺序组织答案。
示例 1:

输入:root = [1,2,3,4,5,6,7], to_delete = [3,5] 输出:[[1,2,null,4],[6],[7]]
示例 2:
输入:root = [1,2,4,null,3], to_delete = [3] 输出:[[1,2,4]]
提示:
- 树中的节点数最大为
1000。 - 每个节点都有一个介于
1到1000之间的值,且各不相同。 to_delete.length <= 1000to_delete包含一些从1到1000、各不相同的值。
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维。
首先,如果在递归过程中修改二叉树结构,必须要让父节点接收递归函数的返回值,因为子树不管删成啥样,都要接到父节点上。
而且,手把手刷二叉树总结篇 说了可以通过函数参数传递父节点传递的数据,所以可以在前序位置判断是否得到了一个新的根节点。
详细题解:
解法代码
class Solution:
def __init__(self):
self.delSet = set()
# 记录森林的根节点
self.res = []
def delNodes(self, root, to_delete):
if root is None:
return []
for d in to_delete:
self.delSet.add(d)
self.doDelete(root, False)
return self.res
# 定义:输入一棵二叉树,删除 delSet 中的节点,返回删除完成后的根节点
def doDelete(self, root, hasParent):
if root is None:
return None
# 判断是否需要被删除
deleted = root.val in self.delSet
if not deleted and not hasParent:
# 没有父节点且不需要被删除,就是一个新的根节点
self.res.append(root)
# 去左右子树进行删除
root.left = self.doDelete(root.left, not deleted)
root.right = self.doDelete(root.right, not deleted)
# 如果需要被删除,返回 null 给父节点
return None if deleted else root可视化
算法可视化面板
技巧一
类似于判断镜像二叉树、翻转二叉树的问题,一般也可以用分解问题的思路,无非就是把整棵树的问题(原问题)分解成子树之间的问题(子问题)。
100. 相同的树
100. 相同的树 | 力扣 | LeetCode | 🟢
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:

输入:p = [1,2,3], q = [1,2,3] 输出:true
示例 2:

输入:p = [1,2], q = [1,null,2] 输出:false
示例 3:

输入:p = [1,2,1], q = [1,1,2] 输出:false
提示:
- 两棵树上的节点数目都在范围
[0, 100]内 -104 <= Node.val <= 104
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维模式。
判断两棵树是否相同,可以分解为判断根节点是否相同,然后判断左右子树的节点是否都相同。
详细题解:
解法代码
class Solution:
# 定义:输入两个根节点,返回以它们为根的两棵二叉树是否相同
def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
# 判断一对节点是否相同
if p is None and q is None:
return True
if p is None or q is None:
return False
if p.val != q.val:
return False
# 判断其他节点是否相同
return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)可视化
算法可视化面板
类似题目:
101. 对称二叉树
101. 对称二叉树 | 力扣 | LeetCode | 🟢
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:

输入:root = [1,2,2,3,4,4,3] 输出:true
示例 2:

输入:root = [1,2,2,null,3,null,3] 输出:false
提示:
- 树中节点数目在范围
[1, 1000]内 -100 <= Node.val <= 100
进阶:你可以运用递归和迭代两种方法解决这个问题吗?
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维模式。
这道题有点像 100.相同的树,你可以对比一下两道题的代码,只不过本题不是让你比较两棵树是否相同,而是让你比较两棵子树是否对称。
那么分解问题的思路就很明显了,判断两棵树是否镜像对称,只要判断两棵子树都是镜像对称的就行了。
如果用迭代的方式,可以使用 BFS 层序遍历,把每一层的节点求出来,然后用左右双指针判断每一层是否是对称的。
详细题解:
解法代码
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if root is None:
return True
# 检查两棵子树是否对称
return self.check(root.left, root.right)
# 定义:判断输入的两棵树是否是镜像对称的
def check(self, left: TreeNode, right: TreeNode) -> bool:
if left is None or right is None:
return left == right
# 两个根节点需要相同
if left.val != right.val:
return False
# 左右子树也需要镜像对称
return self.check(left.right, right.left) and self.check(left.left, right.right)可视化
算法可视化面板
类似题目:
951. 翻转等价二叉树
951. 翻转等价二叉树 | 力扣 | LeetCode | 🟠
我们可以为二叉树 T 定义一个 翻转操作 ,如下所示:选择任意节点,然后交换它的左子树和右子树。
只要经过一定次数的翻转操作后,能使 X 等于 Y,我们就称二叉树 X 翻转 等价 于二叉树 Y。
这些树由根节点 root1 和 root2 给出。如果两个二叉树是否是翻转 等价 的函数,则返回 true ,否则返回 false 。
示例 1:

输入:root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7] 输出:true 解释:我们翻转值为 1,3 以及 5 的三个节点。
示例 2:
输入: root1 = [], root2 = [] 输出: true
示例 3:
输入: root1 = [], root2 = [1] 输出: false
提示:
- 每棵树节点数在
[0, 100]范围内 - 每棵树中的每个值都是唯一的、在
[0, 99]范围内的整数
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维。
如何分解这个问题呢?原问题是两棵二叉树是否是翻转等价的,只要两棵树的根节点能够匹配,那我们就可以去考察这两个根节点的左右子树(共四棵)是否是翻转等价的。
对子树把翻转和不翻转两种情况全都穷举一遍,只要有一种情况能够匹配,就说明整棵树是翻转等价的,具体实现见代码。
详细题解:
解法代码
class Solution:
# 定义:输入两棵二叉树,判断这两棵二叉树是否是翻转等价的
def flipEquiv(self, root1: TreeNode, root2: TreeNode) -> bool:
# 判断 root1 和 root2 两个节点是否能够匹配
if root1 is None and root2 is None:
return True
if root1 is None or root2 is None:
return False
if root1.val != root2.val:
return False
# 根据函数定义,判断子树是否能够匹配
# 不翻转、翻转两种情况满足一种即可算是匹配
return (
# 不翻转子树
self.flipEquiv(root1.left, root2.left) and self.flipEquiv(root1.right, root2.right)
) or (
# 反转子树
self.flipEquiv(root1.left, root2.right) and self.flipEquiv(root1.right, root2.left)
)可视化
算法可视化面板
技巧二
一般来说,遍历的思维模式可以帮你寻找从根节点开始的符合条件的「树枝」,但在不限制起点必须是根节点的条件下,让你寻找符合条件的「树枝」,就需要用到分解问题的思维模式了。
124. 二叉树中的最大路径和
124. 二叉树中的最大路径和 | 力扣 | LeetCode | 🔴
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:

输入:root = [1,2,3] 输出:6 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:

输入:root = [-10,9,20,null,null,15,7] 输出:42 解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
提示:
- 树中节点数目范围是
[1, 3 * 104] -1000 <= Node.val <= 1000
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维。
这题需要巧用二叉树的后序遍历,可以先去做一下 543. 二叉树的直径 和 366. 寻找二叉树的叶子节点。
oneSideMax 函数和上述几道题中都用到的 maxDepth 函数非常类似,只不过 maxDepth 计算最大深度,oneSideMax 计算「单边」最大路径和:
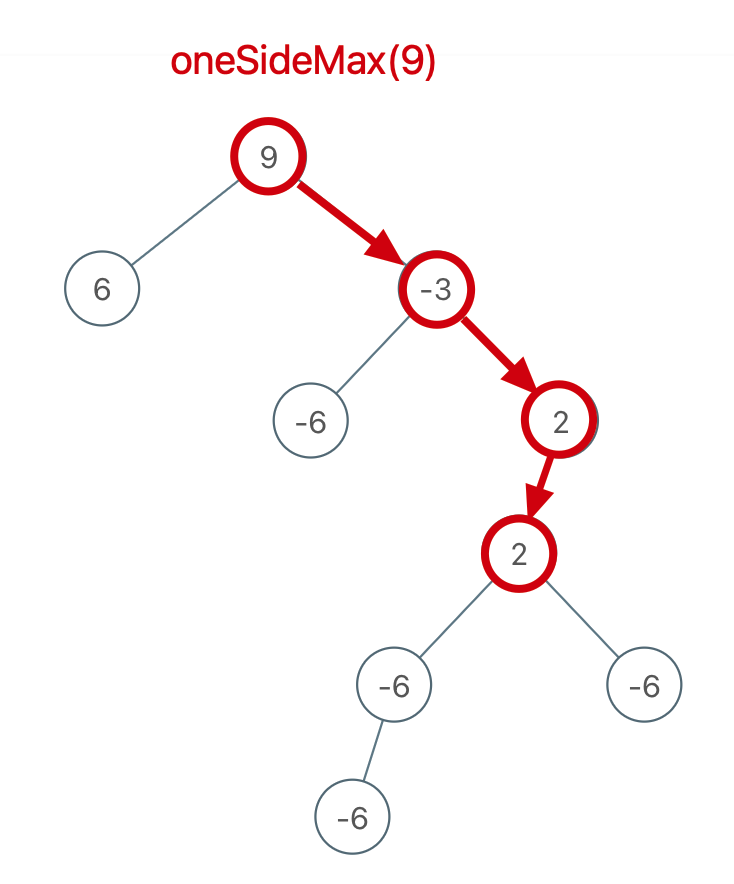
然后在后序遍历的时候顺便计算题目要求的最大路径和。
详细题解:
解法代码
class Solution:
def __init__(self):
self.res = float('-inf')
def maxPathSum(self, root: TreeNode) -> int:
if root is None:
return 0
# 计算单边路径和时顺便计算最大路径和
self.oneSideMax(root)
return self.res
# 定义:计算从根节点 root 为起点的最大单边路径和
def oneSideMax(self, root: TreeNode) -> int:
if root is None:
return 0
left_max_sum = max(0, self.oneSideMax(root.left))
right_max_sum = max(0, self.oneSideMax(root.right))
# 后序遍历位置,顺便更新最大路径和
path_max_sum = root.val + left_max_sum + right_max_sum
self.res = max(self.res, path_max_sum)
# 实现函数定义,左右子树的最大单边路径和加上根节点的值
# 就是从根节点 root 为起点的最大单边路径和
return max(left_max_sum, right_max_sum) + root.val可视化
算法可视化面板
类似题目:
【练习】同时运用两种思维解题
559. N 叉树的最大深度
559. N 叉树的最大深度 | 力扣 | LeetCode | 🟢
给定一个 N 叉树,找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
N 叉树输入按层序遍历序列化表示,每组子节点由空值分隔(请参见示例)。
示例 1:

输入:root = [1,null,3,2,4,null,5,6] 输出:3
示例 2:

输入:root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出:5
提示:
- 树的深度不会超过
1000。 - 树的节点数目位于
[0, 104]之间。
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题可以同时使用两种思维模式,我把两种解法都写一下。
可以对照 104. 二叉树的最大深度 题的解法。
详细题解:
解法代码
# 分解问题的思路
class Solution:
def maxDepth(self, root: 'Node') -> int:
if root is None:
return 0
subTreeMaxDepth = 0
for child in root.children:
subTreeMaxDepth = max(subTreeMaxDepth, self.maxDepth(child))
return 1 + subTreeMaxDepth
# 遍历的思路
class Solution2:
def __init__(self):
# 记录递归遍历到的深度
self.depth = 0
# 记录最大的深度
self.res = 0
def maxDepth(self, root: 'Node') -> int:
self.traverse(root)
return self.res
def traverse(self, root: 'Node'):
if root is None:
return
# 前序遍历位置
self.depth += 1
self.res = max(self.res, self.depth)
for child in root.children:
self.traverse(child)
# 后序遍历位置
self.depth -= 1可视化
算法可视化面板
112. 路径总和
112. 路径总和 | 力扣 | LeetCode | 🟢
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 输出:true 解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:

输入:root = [1,2,3], targetSum = 5 输出:false 解释:树中存在两条根节点到叶子节点的路径: (1 --> 2): 和为 3 (1 --> 3): 和为 4 不存在 sum = 5 的根节点到叶子节点的路径。
示例 3:
输入:root = [], targetSum = 0 输出:false 解释:由于树是空的,所以不存在根节点到叶子节点的路径。
提示:
- 树中节点的数目在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
基本思路
前文 我的刷题经验总结 说过,二叉树的遍历代码是动态规划和回溯算法的祖宗。
动态规划 的关键在于明确递归函数的定义,把用子问题的结果推导出大问题的结果。
回溯算法 就简单粗暴多了,就是单纯的遍历回溯树。
下面给出两种思路下的解法,请仔细体会。
详细题解:
解法代码
class Solution:
# 解法一、分解问题的思路
# 定义:输入一个根节点,返回该根节点到叶子节点是否存在一条和为 targetSum 的路径
def hasPathSum(self, root: TreeNode, targetSum: int) -> bool:
# base case
if root is None:
return False
# root.left == root.right 等同于 root.left == null && root.right == null
if root.left == root.right and root.val == targetSum:
return True
return self.hasPathSum(root.left, targetSum - root.val) or self.hasPathSum(root.right, targetSum - root.val)
# 解法二、遍历二叉树的思路
# 记录遍历过程中的路径和
def hasPathSum_2(self, root: TreeNode, targetSum: int) -> bool:
if root is None:
return False
self.target = targetSum
self.found = False
self.curSum = 0
self.traverse(root)
return self.found
# 二叉树遍历函数
def traverse(self, root: TreeNode) -> None:
if root is None:
return
# 前序遍历位置
self.curSum += root.val
if root.left is None and root.right is None:
if self.curSum == self.target:
self.found = True
self.traverse(root.left)
self.traverse(root.right)
# 后序遍历位置
self.curSum -= root.val可视化
算法可视化面板
113. 路径总和 II
113. 路径总和 II | 力扣 | LeetCode | 🟠
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:[[5,4,11,2],[5,8,4,5]]
示例 2:

输入:root = [1,2,3], targetSum = 5 输出:[]
示例 3:
输入:root = [1,2], targetSum = 0 输出:[]
提示:
- 树中节点总数在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题可以同时运用两种思维。
遍历的思维很简单,只要遍历一遍二叉树,就可以把所有符合条件的路径找出来。为了维护经过的路径,在进入递归的时候要在 path 列表添加节点,结束递归的时候删除节点,类似 回溯算法。
分解问题的思路也不难,你计算以 root 为根的二叉树中和为 sum 的路径,不就可以分解成计算以 root.left, root.right 为根的二叉树中所有和为 sum - root.val 的路径,然后再加上 root 节点吗?
我这里同时写出了遍历思路和分解问题思路的解法,供大家参考。
详细题解:
解法代码
from typing import List, Optional
from collections import deque
class Solution:
def __init__(self):
self.res = []
def pathSum(self, root: Optional[TreeNode], sum: int) -> List[List[int]]:
if root is None:
return self.res
self.traverse(root, sum, deque())
return self.res
# 遍历二叉树
def traverse(self, root: Optional[TreeNode], sum: int, path: deque) -> None:
if root is None:
return
remain = sum - root.val
if root.left is None and root.right is None:
if remain == 0:
# 找到一条路径
path.append(root.val)
self.res.append(list(path))
path.pop()
return
# 维护路径列表
path.append(root.val)
self.traverse(root.left, remain, path)
path.pop()
path.append(root.val)
self.traverse(root.right, remain, path)
path.pop()
# 分解问题的思维模式
class Solution2:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
self.res = []
if root is None:
return self.res
# 如果是叶子节点并且值等于 targetSum,则找到一条路径
if root.left is None and root.right is None and root.val == targetSum:
return [[root.val]]
# 分别递归左右子树,找到子树中和为 targetSum - root.val 的路径
left_answers = self.pathSum(root.left, targetSum - root.val)
right_answers = self.pathSum(root.right, targetSum - root.val)
# 左右子树的路径加上根节点,就是和为 targetSum 的路径
for answer in left_answers:
# 因为底层使用的是 LinkedList,所以这个操作的复杂度是 O(1)
answer.insert(0, root.val)
self.res.append(answer)
for answer in right_answers:
# 因为底层使用的是 LinkedList,所以这个操作的复杂度是 O(1)
answer.insert(0, root.val)
self.res.append(answer)
return self.res可视化
算法可视化面板
类似题目:
617. 合并二叉树
617. 合并二叉树 | 力扣 | LeetCode | 🟢
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:

输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7] 输出:[3,4,5,5,4,null,7]
示例 2:
输入:root1 = [1], root2 = [1,2] 输出:[2,2]
提示:
- 两棵树中的节点数目在范围
[0, 2000]内 -104 <= Node.val <= 104
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题可以同时用到两种思维模式。
虽然输入的是两棵树的根节点,但它们的操作是同步的,所以可以看做是在遍历 root1 这一棵二叉树,顺便把 root2 的节点合并过来。下面我给出两种思维模式的解法代码,具体看注释吧。
详细题解:
解法代码
class Solution:
# 分解问题的思维模式
# 定义:输入两棵树的根节点,返回合并后的树的根节点
def mergeTrees(self, root1: TreeNode, root2: TreeNode) -> TreeNode:
# 如果一棵树非空,那么合并后就是另一棵树
if root1 is None:
return root2
if root2 is None:
return root1
# 两棵树都有的节点,叠加节点值
root1.val += root2.val
# 利用函数定义,子树合并后接到
root1.left = self.mergeTrees(root1.left, root2.left)
root1.right = self.mergeTrees(root1.right, root2.right)
return root1
class Solution2:
# 遍历的思维模式
def mergeTrees(self, root1: TreeNode, root2: TreeNode) -> TreeNode:
if root1 is None:
return root2
# 遍历 root1,顺便把 root2 的节点合并过来
self.traverse(root1, root2)
return root1
def traverse(self, root1: TreeNode, root2: TreeNode):
if root1 is None or root2 is None:
return
if root1 is not None and root2 is not None:
# 两棵树都有的节点,叠加节点值
root1.val += root2.val
# 如果 root1 没有子树而 root2 有,那么就把 root2 的子树接到 root1 上
# 注意接完之后把 root2 的子树置为 null,免得错误计算节点累加值
if root1.left is None and root2.left is not None:
root1.left = root2.left
root2.left = None
if root1.right is None and root2.right is not None:
root1.right = root2.right
root2.right = None
# 递归遍历左右子节点,root2 的节点也跟着同步移动
self.traverse(root1.left, root2.left)
self.traverse(root1.right, root2.right)可视化
算法可视化面板
897. 递增顺序搜索树
897. 递增顺序搜索树 | 力扣 | LeetCode | 🟢
给你一棵二叉搜索树的 root ,请你 按中序遍历 将其重新排列为一棵递增顺序搜索树,使树中最左边的节点成为树的根节点,并且每个节点没有左子节点,只有一个右子节点。
示例 1:

输入:root = [5,3,6,2,4,null,8,1,null,null,null,7,9] 输出:[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
示例 2:

输入:root = [5,1,7] 输出:[1,null,5,null,7]
提示:
- 树中节点数的取值范围是
[1, 100] 0 <= Node.val <= 1000
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题可以同时用到两种思维模式。
「遍历」的话很简单,你对 BST 做中序遍历,其结果就是有序的,重新构造出题目要求的这个类似链表的二叉树即可。
「分解问题」的思路也不难,你只要做过 114. 二叉树展开为链表 这道题,稍微改下解法就可以解决这道题了,明确 increasingBST 的定义,然后利用这个定义进行操作即可。
这里我给出分解问题的解法思路。
详细题解:
解法代码
# 输入一棵 BST,返回一个有序「链表」
class Solution:
def increasingBST(self, root: TreeNode) -> TreeNode:
if root is None:
return None
# 先把左右子树拉平
left = self.increasingBST(root.left)
root.left = None
right = self.increasingBST(root.right)
root.right = right
# 左子树为空的话,就不用处理了
if left is None:
return root
# 左子树非空,需要把根节点和右子树接到左子树末尾
p = left
while p is not None and p.right is not None:
p = p.right
p.right = root
return left可视化
算法可视化面板
类似题目:
938. 二叉搜索树的范围和
938. 二叉搜索树的范围和 | 力扣 | LeetCode | 🟢
给定二叉搜索树的根结点 root,返回值位于范围 [low, high] 之间的所有结点的值的和。
示例 1:

输入:root = [10,5,15,3,7,null,18], low = 7, high = 15 输出:32
示例 2:

输入:root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10 输出:23
提示:
- 树中节点数目在范围
[1, 2 * 104]内 1 <= Node.val <= 1051 <= low <= high <= 105- 所有
Node.val互不相同
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题可以同时使用这两种思维模式。
遍历的思路就是单纯用 traverse 函数遍历一遍 BST,找到落在区间的元素。分解问题的思路关键是要明确函数定义,然后利用这个定义。
详细题解:
解法代码
class Solution:
# 遍历的思路
def __init__(self):
self.sum = 0
def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:
if root is None:
return 0
# 遍历一遍 BST 计算区间元素和
self.traverse(root, low, high)
return self.sum
def traverse(self, root: TreeNode, low: int, high: int):
if root is None:
return
if root.val < low:
# 目标区间在右子树
self.traverse(root.right, low, high)
elif root.val > high:
# 目标区间在左子树
self.traverse(root.left, low, high)
else:
# root.val 落在目标区间,累加 sum
self.sum += root.val
# 继续遍历左右子树
self.traverse(root.right, low, high)
self.traverse(root.left, low, high)
class Solution2:
# 分解问题的思路
# 定义:输入一个 BST,计算值落在 [low, high] 之间的元素之和
def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:
if root is None:
return 0
if root.val < low:
# 目标区间在右子树
return self.rangeSumBST(root.right, low, high)
elif root.val > high:
# 目标区间在左子树
return self.rangeSumBST(root.left, low, high)
else:
# 以 root 为根的这棵 BST 落在 [low, high] 之间的元素之和,
# 等于 root.val 加上左右子树落在区间的元素之和
return root.val + self.rangeSumBST(root.left, low, high) + self.rangeSumBST(root.right, low, high)可视化
算法可视化面板
1379. 找出克隆二叉树中的相同节点
1379. 找出克隆二叉树中的相同节点 | 力扣 | LeetCode | 🟢
给你两棵二叉树,原始树 original 和克隆树 cloned,以及一个位于原始树 original 中的目标节点 target。
其中,克隆树 cloned 是原始树 original 的一个 副本 。
请找出在树 cloned 中,与 target 相同 的节点,并返回对该节点的引用(在 C/C++ 等有指针的语言中返回 节点指针,其他语言返回节点本身)。
注意:你 不能 对两棵二叉树,以及 target 节点进行更改。只能 返回对克隆树 cloned 中已有的节点的引用。
示例 1:

输入: tree = [7,4,3,null,null,6,19], target = 3 输出: 3 解释: 上图画出了树 original 和 cloned。target 节点在树 original 中,用绿色标记。答案是树 cloned 中的黄颜色的节点(其他示例类似)。
示例 2:

输入: tree = [7], target = 7 输出: 7
示例 3:

输入: tree = [8,null,6,null,5,null,4,null,3,null,2,null,1], target = 4 输出: 4
提示:
- 树中节点的数量范围为
[1, 104]。 - 同一棵树中,没有值相同的节点。
target节点是树original中的一个节点,并且不会是null。
进阶:如果树中允许出现值相同的节点,将如何解答?
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题可以同时用到两种思维。
说白了,这道题就是让你从一棵二叉树中搜索一个目标节点,考虑到题目的 follow up 问你节点的值存在重复的情况,所以用对比节点引用的方式进行比较。
详细题解:
解法代码
# 遍历的思路
class Solution:
# 定义:找到 original 中 target 节点在 cloned 树中对应的节点
def getTargetCopy(self, original: TreeNode, cloned: TreeNode, target: TreeNode) -> TreeNode:
self.target = target
self.res = None
self.traverse(original, cloned)
return self.res
# 二叉树遍历函数
def traverse(self, original: TreeNode, cloned: TreeNode):
if original is None or self.res is not None:
return
if original == self.target:
self.res = cloned
return
# 二叉树遍历框架
self.traverse(original.left, cloned.left)
self.traverse(original.right, cloned.right)
# 分解问题的思路
class Solution2:
# 定义:找到 original 中 target 节点在 cloned 树中对应的节点
def getTargetCopy(self, original: TreeNode, cloned: TreeNode, target: TreeNode) -> TreeNode:
if original is None:
return None
# 找到目标节点
if target == original:
return cloned
# 去左子树找
left = self.getTargetCopy(original.left, cloned.left, target)
if left is not None:
return left
# 左子树找不到的话去右子树找
return self.getTargetCopy(original.right, cloned.right, target)可视化
算法可视化面板
【练习】利用后序位置解题 I
有些题目,你按照拍脑袋的方式去做,可能发现需要在递归代码中调用其他递归函数计算字数的信息。一般来说,出现这种情况时你可以考虑用后序遍历的思维方式来优化算法,利用后序遍历传递子树的信息,避免过高的时间复杂度。
像求和、求高度这种基本的二叉树函数很容易写,有时候只要在它们的后序位置添加一点代码,就能得到我们想要的答案。
110. 平衡二叉树
110. 平衡二叉树 | 力扣 | LeetCode | 🟢
给定一个二叉树,判断它是否是 平衡二叉树
示例 1:

输入:root = [3,9,20,null,null,15,7] 输出:true
示例 2:

输入:root = [1,2,2,3,3,null,null,4,4] 输出:false
示例 3:
输入:root = [] 输出:true
提示:
- 树中的节点数在范围
[0, 5000]内 -104 <= Node.val <= 104
基本思路
这里要用到前文 手把手刷二叉树总结篇 说过的后序位置的妙用。
一般的拍脑袋思路是,遍历二叉树,然后对每一个节点计算左右的最大高度。
但是计算一棵二叉树的最大深度也需要递归遍历这棵树的所有节点,如果对每个节点都算一遍最大深度,时间复杂度是比较高的。
所以最好的解法是反过来思考,只计算一次最大深度,计算的过程中在后序遍历位置顺便判断二叉树是否平衡:
对于每个节点,先算出来左右子树的最大高度,然后在后序遍历的位置根据左右子树的最大高度判断平衡性。
详细题解:
解法代码
class Solution:
def __init__(self):
# 记录二叉树是否平衡
self.balanced = True
def isBalanced(self, root: TreeNode) -> bool:
self.maxDepth(root)
return self.balanced
# 输入一个节点,返回以该节点为根的二叉树的最大深度
def maxDepth(self, root: TreeNode) -> int:
if root is None:
return 0
# if not self.balanced:
# 随便返回一个值即可,旨在结束递归
# return -666
leftMaxDepth = self.maxDepth(root.left)
rightMaxDepth = self.maxDepth(root.right)
# 后序遍历位置
# 如果左右最大深度大于 1,就不是平衡二叉树
if abs(rightMaxDepth - leftMaxDepth) > 1:
self.balanced = False
return 1 + max(leftMaxDepth, rightMaxDepth)可视化
算法可视化面板
类似题目:
508. 出现次数最多的子树元素和
508. 出现次数最多的子树元素和 | 力扣 | LeetCode | 🟠
给你一个二叉树的根结点 root ,请返回出现次数最多的子树元素和。如果有多个元素出现的次数相同,返回所有出现次数最多的子树元素和(不限顺序)。
一个结点的 「子树元素和」 定义为以该结点为根的二叉树上所有结点的元素之和(包括结点本身)。
示例 1:

输入: root = [5,2,-3] 输出: [2,-3,4]
示例 2:

输入: root = [5,2,-5] 输出: [2]
提示:
- 节点数在
[1, 104]范围内 -105 <= Node.val <= 105
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维,同时要利用后序位置来计算答案。
sum 函数根据子树的元素和推导出原树的所有元素和,只不过在后序遍历位置添加一些统计工作,便于找出出现频率最高的子树和。
详细题解:
解法代码
class Solution:
# sum -> count
def __init__(self):
self.sum_to_count = {}
def findFrequentTreeSum(self, root):
# traverse the binary tree and record all subtree sums and their frequencies
self.sum(root)
# find the highest frequency
max_count = max(self.sum_to_count.values(), default=0)
# find the subtree sums that have the highest frequency
res = [key for key, count in self.sum_to_count.items() if count == max_count]
# convert to a python list
return res
# definition: given a node, return the sum of all nodes in the subtree rooted at that node
def sum(self, root):
if not root:
return 0
left_sum = self.sum(root.left)
right_sum = self.sum(root.right)
res = root.val + left_sum + right_sum
# postorder traversal position, record the frequency of the subtree sum
self.sum_to_count[res] = self.sum_to_count.get(res, 0) + 1
return res可视化
算法可视化面板
563. 二叉树的坡度
563. 二叉树的坡度 | 力扣 | LeetCode | 🟢
给你一个二叉树的根节点 root ,计算并返回 整个树 的坡度 。
一个树的 节点的坡度 定义即为,该节点左子树的节点之和和右子树节点之和的 差的绝对值 。如果没有左子树的话,左子树的节点之和为 0 ;没有右子树的话也是一样。空结点的坡度是 0 。
整个树 的坡度就是其所有节点的坡度之和。
示例 1:

输入:root = [1,2,3] 输出:1 解释: 节点 2 的坡度:|0-0| = 0(没有子节点) 节点 3 的坡度:|0-0| = 0(没有子节点) 节点 1 的坡度:|2-3| = 1(左子树就是左子节点,所以和是 2 ;右子树就是右子节点,所以和是 3 ) 坡度总和:0 + 0 + 1 = 1
示例 2:

输入:root = [4,2,9,3,5,null,7] 输出:15 解释: 节点 3 的坡度:|0-0| = 0(没有子节点) 节点 5 的坡度:|0-0| = 0(没有子节点) 节点 7 的坡度:|0-0| = 0(没有子节点) 节点 2 的坡度:|3-5| = 2(左子树就是左子节点,所以和是 3 ;右子树就是右子节点,所以和是 5 ) 节点 9 的坡度:|0-7| = 7(没有左子树,所以和是 0 ;右子树正好是右子节点,所以和是 7 ) 节点 4 的坡度:|(3+5+2)-(9+7)| = |10-16| = 6(左子树值为 3、5 和 2 ,和是 10 ;右子树值为 9 和 7 ,和是 16 ) 坡度总和:0 + 0 + 0 + 2 + 7 + 6 = 15
示例 3:

输入:root = [21,7,14,1,1,2,2,3,3] 输出:9
提示:
- 树中节点数目的范围在
[0, 104]内 -1000 <= Node.val <= 1000
基本思路
这里要用到前文 手把手刷二叉树总结篇 说过的后序位置的妙用。
sum 函数记录二叉树的节点之和,在后序位置顺便计算二叉树的「坡度」即可。
详细题解:
解法代码
class Solution:
def __init__(self):
self.res = 0
# 定义:输入一棵二叉树,返回这棵二叉树所有元素的和
def sum(self, root: TreeNode) -> int:
if root is None:
return 0
left_sum = self.sum(root.left)
right_sum = self.sum(root.right)
# 后序位置
self.res += abs(left_sum - right_sum)
return left_sum + right_sum + root.val
def findTilt(self, root: TreeNode) -> int:
self.sum(root)
return self.res可视化
算法可视化面板
814. 二叉树剪枝
814. 二叉树剪枝 | 力扣 | LeetCode | 🟠
给你二叉树的根结点 root ,此外树的每个结点的值要么是 0 ,要么是 1 。
返回移除了所有不包含 1 的子树的原二叉树。
节点 node 的子树为 node 本身加上所有 node 的后代。
示例 1:

输入:root = [1,null,0,0,1] 输出:[1,null,0,null,1] 解释: 只有红色节点满足条件“所有不包含 1 的子树”。 右图为返回的答案。
示例 2:

输入:root = [1,0,1,0,0,0,1] 输出:[1,null,1,null,1]
示例 3:

输入:root = [1,1,0,1,1,0,1,0] 输出:[1,1,0,1,1,null,1]
提示:
- 树中节点的数目在范围
[1, 200]内 Node.val为0或1
基本思路
建议先做一下 543. 二叉树的直径 和 687. 最长同值路径,理解后序遍历位置的特殊性。
这道题的难点在于要一直剪枝,直到没有值为 0 的叶子节点为止,只有从后序遍历位置自底向上处理才能获得最高的效率。
详细题解:
解法代码
class Solution:
# 定义:输入一棵二叉树,返回的二叉树叶子节点都是 1
def pruneTree(self, root: TreeNode) -> TreeNode:
if root is None:
return None
# 二叉树递归框架
root.left = self.pruneTree(root.left)
root.right = self.pruneTree(root.right)
# 后序遍历位置,判断自己是否是值为 0 的叶子节点
if root.val == 0 and root.left is None and root.right is None:
# 返回值会被父节点接收,相当于把自己删掉了
return None
# 如果不是,正常返回
return root可视化
算法可视化面板
类似题目:
1325. 删除给定值的叶子节点
1325. 删除给定值的叶子节点 | 力扣 | LeetCode | 🟠
给你一棵以 root 为根的二叉树和一个整数 target ,请你删除所有值为 target 的 叶子节点 。
注意,一旦删除值为 target 的叶子节点,它的父节点就可能变成叶子节点;如果新叶子节点的值恰好也是 target ,那么这个节点也应该被删除。
也就是说,你需要重复此过程直到不能继续删除。
示例 1:

输入:root = [1,2,3,2,null,2,4], target = 2 输出:[1,null,3,null,4] 解释: 上面左边的图中,绿色节点为叶子节点,且它们的值与 target 相同(同为 2 ),它们会被删除,得到中间的图。 有一个新的节点变成了叶子节点且它的值与 target 相同,所以将再次进行删除,从而得到最右边的图。
示例 2:

输入:root = [1,3,3,3,2], target = 3 输出:[1,3,null,null,2]
示例 3:

输入:root = [1,2,null,2,null,2], target = 2 输出:[1] 解释:每一步都删除一个绿色的叶子节点(值为 2)。
提示:
- 树中节点数量的范围是
[1, 3000]。 1 <= Node.val, target <= 1000
基本思路
删除指定值的叶子节点,其实就是遍历所有的叶子节点,然后判断是否需要删除;删除叶子节点也很简单,return null 让父节点接收即可。
难点在于他这个删除操作是循环的,一直删到叶子结点不存在 target 为止。这里要用到前文 手把手刷二叉树总结篇 说过的后序位置的妙用了:
一个节点要在后序位置接收左右子树的返回值,才能知道自己的叶子节点是否都被删掉了,以此判断自己是不是变成了叶子节点。
这个考点在 814. 二叉树剪枝 中也有体现,没做过的读者建议去做一下,解法的关键点在于利用后序遍历特点,在后序遍历位置每个节点可以直到自己是否需要被删除。
详细题解:
解法代码
class Solution:
def removeLeafNodes(self, root: TreeNode, target: int) -> TreeNode:
if root is None:
return None
# 二叉树递归框架
# 如果左右子节点需要被删除,先递归删除它们
root.left = self.removeLeafNodes(root.left, target)
root.right = self.removeLeafNodes(root.right, target)
# 后序遍历位置,此时节点 root 直到自己是否需要被删除
if root.val == target and root.left is None and root.right is None:
return None
return root可视化
算法可视化面板
687. 最长同值路径
687. 最长同值路径 | 力扣 | LeetCode | 🟠
给定一个二叉树的 root ,返回 最长的路径的长度 ,这个路径中的 每个节点具有相同值 。 这条路径可以经过也可以不经过根节点。
两个节点之间的路径长度 由它们之间的边数表示。
示例 1:

输入:root = [5,4,5,1,1,5] 输出:2
示例 2:

输入:root = [1,4,5,4,4,5] 输出:2
提示:
- 树的节点数的范围是
[0, 104] -1000 <= Node.val <= 1000- 树的深度将不超过
1000
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维,而且这类题目需要利用二叉树的后序遍历。
做这题之前,我建议你先做 543. 二叉树的直径 题并进行对比,把那道题的最大深度函数 maxDepth 的定义带入到这道题中,maxLen 相当于求值为 parentVal 的节点的最大深度。配合代码注释就立马明白了。
详细题解:
解法代码
class Solution:
def __init__(self):
self.res = 0
def longestUnivaluePath(self, root):
if root is None:
return 0
# 在后序遍历的位置更新 res
self.maxLen(root, root.val)
return self.res
# 定义:计算以 root 为根的这棵二叉树中,从 root 开始值为 parentVal 的最长树枝长度
def maxLen(self, root, parentVal):
if root is None:
return 0
# 利用函数定义,计算左右子树值为 root.val 的最长树枝长度
leftLen = self.maxLen(root.left, root.val)
rightLen = self.maxLen(root.right, root.val)
# 后序遍历位置顺便更新全局变量
# 同值路径就是左右同值树枝长度之和
self.res = max(self.res, leftLen + rightLen)
# 如果 root 本身和上级值不同,那么整棵子树都不可能有同值树枝
if root.val != parentVal:
return 0
# 实现函数的定义:
# 以 root 为根的二叉树从 root 开始值为 parentVal 的最长树枝长度
# 等于左右子树的最长树枝长度的最大值加上 root 节点本身
return 1 + max(leftLen, rightLen)可视化
算法可视化面板
类似题目:
865. 具有所有最深节点的最小子树
865. 具有所有最深节点的最小子树 | 力扣 | LeetCode | 🟠
给定一个根为 root 的二叉树,每个节点的深度是 该节点到根的最短距离 。
返回包含原始树中所有 最深节点 的 最小子树 。
如果一个节点在 整个树 的任意节点之间具有最大的深度,则该节点是 最深的 。
一个节点的 子树 是该节点加上它的所有后代的集合。
示例 1:

输入:root = [3,5,1,6,2,0,8,null,null,7,4] 输出:[2,7,4] 解释: 我们返回值为 2 的节点,在图中用黄色标记。 在图中用蓝色标记的是树的最深的节点。 注意,节点 5、3 和 2 包含树中最深的节点,但节点 2 的子树最小,因此我们返回它。
示例 2:
输入:root = [1] 输出:[1] 解释:根节点是树中最深的节点。
示例 3:
输入:root = [0,1,3,null,2] 输出:[2] 解释:树中最深的节点为 2 ,有效子树为节点 2、1 和 0 的子树,但节点 2 的子树最小。
提示:
- 树中节点的数量在
[1, 500]范围内。 0 <= Node.val <= 500- 每个节点的值都是 独一无二 的。
注意:本题与力扣 1123 重复:https://leetcode-cn.com/problems/lowest-common-ancestor-of-deepest-leaves
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维,而且涉及处理子树,需要用后序遍历。
说到底,这道题就是让你求那些「最深」的叶子节点的最近公共祖先,可以看下后文 二叉树最近公共祖先。
你想想,一个节点需要知道哪些信息,才能确定自己是最深叶子节点的最近公共祖先?
它需要知道自己的左右子树的最大深度:如果左右子树一样深,那么当前节点就是最近公共祖先;如果左右子树不一样深,那么最深叶子节点的最近公共祖先肯定在左右子树上。
所以我们新建一个 Result 类,存放左右子树的最大深度及叶子节点的最近公共祖先节点,其余逻辑类似 104. 二叉树的最大深度。
详细题解:
解法代码
class Solution:
class Result:
def __init__(self, node, depth):
# 记录最近公共祖先节点 node
self.node = node
# 记录以 node 为根的二叉树最大深度
self.depth = depth
def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:
res = self.maxDepth(root)
return res.node
# 定义:输入一棵二叉树,返回该二叉树的最大深度以及最深叶子节点的最近公共祖先节点
def maxDepth(self, root: TreeNode) -> 'Solution.Result':
if root is None:
return self.Result(None, 0)
left = self.maxDepth(root.left)
right = self.maxDepth(root.right)
if left.depth == right.depth:
# 当左右子树的最大深度相同时,这个根节点是新的最近公共祖先
# 以当前 root 节点为根的子树深度是子树深度 + 1
return self.Result(root, left.depth + 1)
# 左右子树的深度不同,则最近公共祖先在 depth 较大的一边
res = left if left.depth > right.depth else right
# 正确维护二叉树的最大深度
res.depth += 1
return res可视化
算法可视化面板
类似题目:
1026. 节点与其祖先之间的最大差值
1026. 节点与其祖先之间的最大差值 | 力扣 | LeetCode | 🟠
给定二叉树的根节点 root,找出存在于 不同 节点 A 和 B 之间的最大值 V,其中 V = |A.val - B.val|,且 A 是 B 的祖先。
(如果 A 的任何子节点之一为 B,或者 A 的任何子节点是 B 的祖先,那么我们认为 A 是 B 的祖先)
示例 1:

输入:root = [8,3,10,1,6,null,14,null,null,4,7,13] 输出:7 解释: 我们有大量的节点与其祖先的差值,其中一些如下: |8 - 3| = 5 |3 - 7| = 4 |8 - 1| = 7 |10 - 13| = 3 在所有可能的差值中,最大值 7 由 |8 - 1| = 7 得出。
示例 2:

输入:root = [1,null,2,null,0,3] 输出:3
提示:
- 树中的节点数在
2到5000之间。 0 <= Node.val <= 105
基本思路
这题要用到 手把手刷二叉树总结篇 中强调的二叉树后序位置的特殊性。
站在某个节点,你如何判断以这个节点为根的二叉树中的最大差值?换句话说,你需要知道哪些信息,才能算出来这个最大差值?
思考这个问题很有必要,你必须先知道怎么算,才能写递归函数去实现你的思路。
这个问题的答案是,每个节点需要知道左右子树的最小值和最大值,然后就能算出「以自己为祖先」的最大差值。
每个节点都知道以自己为祖先的最大差值,那么所有这些差值中最大的那个就是整棵树的最大差值,这个取最大值的过程需要在后序遍历的位置进行,直接看解法代码理解吧。
详细题解:
解法代码
class Solution:
def maxAncestorDiff(self, root: TreeNode) -> int:
self.getMinMax(root)
return self.res
res = 0
# 定义:输入一棵二叉树,返回该二叉树中节点的最小值和最大值,
# 第一个元素是最小值,第二个值是最大值
def getMinMax(self, root: TreeNode) -> List[int]:
if root is None:
return [float('inf'), float('-inf')]
leftMinMax = self.getMinMax(root.left)
rightMinMax = self.getMinMax(root.right)
# 以 root 为根的这棵树的最大值和最小值可以通过左右子树的最大最小值推导出来
rootMin = min(root.val, leftMinMax[0], rightMinMax[0])
rootMax = max(root.val, leftMinMax[1], rightMinMax[1])
# 在后序位置顺便判断所有差值的最大值
self.res = max(self.res, rootMax - root.val, root.val - rootMin)
return [rootMin, rootMax]可视化
算法可视化面板
1339. 分裂二叉树的最大乘积
1339. 分裂二叉树的最大乘积 | 力扣 | LeetCode | 🟠
给你一棵二叉树,它的根为 root 。请你删除 1 条边,使二叉树分裂成两棵子树,且它们子树和的乘积尽可能大。
由于答案可能会很大,请你将结果对 10^9 + 7 取模后再返回。
示例 1:

输入:root = [1,2,3,4,5,6] 输出:110 解释:删除红色的边,得到 2 棵子树,和分别为 11 和 10 。它们的乘积是 110 (11*10)
示例 2:

输入:root = [1,null,2,3,4,null,null,5,6] 输出:90 解释:移除红色的边,得到 2 棵子树,和分别是 15 和 6 。它们的乘积为 90 (15*6)
示例 3:
输入:root = [2,3,9,10,7,8,6,5,4,11,1] 输出:1025
示例 4:
输入:root = [1,1] 输出:1
提示:
- 每棵树最多有
50000个节点,且至少有2个节点。 - 每个节点的值在
[1, 10000]之间。
基本思路
这里要用到前文 手把手刷二叉树总结篇 说过的后序位置的妙用。
题目说的比较繁琐,这道题说的简单些就是:
在二叉树中切出一个小二叉树(子树),计算这个子树节点之和与剩下的节点之和的乘积。
想求最大乘积,那就穷举,把所有可能的切法都穷举一遍,计算乘积。
任何子树的节点之和都可以在后序位置获得,而剩下的其他节点之和就是整棵二叉树的节点之和减去子树节点之和。
所以我们写一个 getSum 函数,先执行一遍计算整棵树的节点之和,然后再调用一次利用它的后序位置计算乘积。
详细题解:
解法代码
class Solution:
def maxProduct(self, root: TreeNode) -> int:
# 先利用求和函数得到整棵树的节点之和
self.treeSum = self.getSum(root)
# 再次调用,利用后序位置计算子树之积
self.getSum(root)
return int(self.res % (1e9 + 7))
def __init__(self):
self.res = 0
self.treeSum = 0
def getSum(self, root: TreeNode) -> int:
if root is None:
return 0
leftSum = self.getSum(root.left)
rightSum = self.getSum(root.right)
rootSum = leftSum + rightSum + root.val
# 后序位置计算乘积
self.res = max(self.res, rootSum * (self.treeSum - rootSum))
return rootSum类似题目:
1372. 二叉树中的最长交错路径
1372. 二叉树中的最长交错路径 | 力扣 | LeetCode | 🟠
给你一棵以 root 为根的二叉树,二叉树中的交错路径定义如下:
- 选择二叉树中 任意 节点和一个方向(左或者右)。
- 如果前进方向为右,那么移动到当前节点的的右子节点,否则移动到它的左子节点。
- 改变前进方向:左变右或者右变左。
- 重复第二步和第三步,直到你在树中无法继续移动。
交错路径的长度定义为:访问过的节点数目 - 1(单个节点的路径长度为 0 )。
请你返回给定树中最长 交错路径 的长度。
示例 1:

输入:root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1] 输出:3 解释:蓝色节点为树中最长交错路径(右 -> 左 -> 右)。
示例 2:

输入:root = [1,1,1,null,1,null,null,1,1,null,1] 输出:4 解释:蓝色节点为树中最长交错路径(左 -> 右 -> 左 -> 右)。
示例 3:
输入:root = [1] 输出:0
提示:
- 每棵树最多有
50000个节点。 - 每个节点的值在
[1, 100]之间。
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维,而且要用到后序位置的妙用。
首先,我们先明确一下名词的含义,便于讲解:
如果一个从上到下的交错路径的开头是从右到左的,称之为「左交错路径」,反之成为「右交错路径」。
这样的话,一个节点 x 能够产生的交错路径就能分解到左右子树:
1、x 的左子树的「右交错路径」+ 节点 x = x 的「左交错路径」
2、x 的右子树的「左交错路径」+ 节点 x = x 的「右交错路径」
比较 x 的左右交错路径,即可算出以 x 开头的最长交错路径。
对二叉树上的所有节点计算交错路径长度,即可得到最长的交错路径长度。
所以我们定义一个 getPathLen 函数计算并返回一个节点的左右交错路径长度,然后在后序位置上更新全局最大值。
详细题解:
解法代码
class Solution:
def longestZigZag(self, root: TreeNode) -> int:
self.res = 0
self.getPathLen(root)
return self.res
# 输入二叉树的根节点 root,返回两个值
# 第一个是从 root 开始向左走的最长交错路径长度,
# 第一个是从 root 开始向右走的最长交错路径长度
def getPathLen(self, root: TreeNode) -> tuple:
if root is None:
return (-1, -1)
left = self.getPathLen(root.left)
right = self.getPathLen(root.right)
# 后序位置,根据左右子树的交错路径长度推算根节点的交错路径长度
rootPathLen1 = left[1] + 1
rootPathLen2 = right[0] + 1
# 更新全局最大值
self.res = max(self.res, max(rootPathLen1, rootPathLen2))
return (rootPathLen1, rootPathLen2)可视化
算法可视化面板
606. 根据二叉树创建字符串
606. 根据二叉树创建字符串 | 力扣 | LeetCode | 🟠
给你二叉树的根节点 root ,请你采用前序遍历的方式,将二叉树转化为一个由括号和整数组成的字符串,返回构造出的字符串。
空节点使用一对空括号对 "()" 表示,转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。
示例 1:

输入:root = [1,2,3,4] 输出:"1(2(4))(3)" 解释:初步转化后得到 "1(2(4)())(3()())" ,但省略所有不必要的空括号对后,字符串应该是"1(2(4))(3)" 。
示例 2:

输入:root = [1,2,3,null,4] 输出:"1(2()(4))(3)" 解释:和第一个示例类似,但是无法省略第一个空括号对,否则会破坏输入与输出一一映射的关系。
提示:
- 树中节点的数目范围是
[1, 104] -1000 <= Node.val <= 1000
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维。
我们先明确 tree2str 函数的定义,然后利用这个定义生成左右子树的字符串,然后结合 root 组装出最后结果。
注意,题目说按照前序遍历的方式组装字符串,但我们必须在后序遍历位置去组装,因为只有那里你才能拿到左右子树的字符串。
详细题解:
解法代码
class Solution:
# 定义:输入以 root 的二叉树,返回描述该二叉树的字符串
def tree2str(self, root: TreeNode) -> str:
# base case
if root is None:
return ""
if root.left is None and root.right is None:
return str(root.val)
# 递归生成左右子树的字符串
left_str = self.tree2str(root.left)
right_str = self.tree2str(root.right)
# 后序代码位置
# 根据左右子树字符串组装出前序遍历的顺序
# 按题目要求处理 root 只有一边有子树的情况
if root.left is not None and root.right is None:
# 省略空的右子树
return f"{root.val}({left_str})"
if root.left is None and root.right is not None:
# 空的左子树不能省略
return f"{root.val}()({right_str})"
# 按题目要求处理 root 左右子树都不空的情况
return f"{root.val}({left_str})({right_str})"可视化
算法可视化面板
1443. 收集树上所有苹果的最少时间
1443. 收集树上所有苹果的最少时间 | 力扣 | LeetCode | 🟠
给你一棵有 n 个节点的无向树,节点编号为 0 到 n-1 ,它们中有一些节点有苹果。通过树上的一条边,需要花费 1 秒钟。你从 节点 0 出发,请你返回最少需要多少秒,可以收集到所有苹果,并回到节点 0 。
无向树的边由 edges 给出,其中 edges[i] = [fromi, toi] ,表示有一条边连接 from 和 toi 。除此以外,还有一个布尔数组 hasApple ,其中 hasApple[i] = true 代表节点 i 有一个苹果,否则,节点 i 没有苹果。
示例 1:

输入:n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false] 输出:8 解释:上图展示了给定的树,其中红色节点表示有苹果。一个能收集到所有苹果的最优方案由绿色箭头表示。
示例 2:

输入:n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false] 输出:6 解释:上图展示了给定的树,其中红色节点表示有苹果。一个能收集到所有苹果的最优方案由绿色箭头表示。
示例 3:
输入:n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false] 输出:0
提示:
1 <= n <= 10^5edges.length == n - 1edges[i].length == 20 <= ai < bi <= n - 1hasApple.length == n
基本思路
这里要用到前文 手把手刷二叉树总结篇 说过的后序位置的妙用。
题目输入的是若干条边的形式,我们首先需要用 图论算法基础 中讲到的表示无向图的邻接表来存储这棵多叉树。
构造出了多叉树,这道题显然要用分解问题的思维模式,并利用后序位置的妙用。
为什么?假设你站在这棵树中的某个节点上,你脚底下有多棵子树,你要去这些子树里面找苹果对不对?
你如果知道了在一棵子树中找苹果的最小步数,假设为 x,那么算上你进出这棵子树的 2 步,x + 2 就是从你进入这棵子树找苹果的最小步数。
当然,你脚底下可能有多棵子树都有苹果,所以就会有 x1 + 2, x2 + 2... 这些结果加起来,不就是在以你这个节点为根的整棵树找苹果的最小步数了么?这分解问题的思路不就出来了么?
把上述思路翻译出来即可,注意递归函数 collect 的定义,我们需要对没有苹果的情况给个特殊值,具体看代码吧。
详细题解:
解法代码
class Solution:
# 邻接表形式,存储着一棵多叉树
def __init__(self):
self.graph = {}
self.visited = set()
def minTime(self, n: int, edges: List[List[int]], hasApple: List[bool]) -> int:
# 构造多叉树结构
for i in range(n):
self.graph[i] = []
for a, b in edges:
self.graph[a].append(b)
self.graph[b].append(a)
# 根据 collect 函数的定义,返回题目想要的结果
self.hasApple = hasApple # Adding this line to fix the NameError
res = self.collect(0)
return res if res != -1 else 0
# 定义:遍历以 root 为根的这棵多叉树,返回收集其中的所有苹果所需的最少步数(时间)
# 如果返回的是 -1,说明以 root 为根的这棵多叉树中没有苹果
def collect(self, root: int) -> int:
if root in self.visited:
return -1
self.visited.add(root)
# 去子树看看是否找到了苹果
sum_time = 0 # Renamed sum to sum_time to avoid conflict with built-in sum function
for child in self.graph[root]:
subTime = self.collect(child)
if subTime != -1:
# 这棵子树中有苹果,从 root 进入和离开这棵子树,需要额外的两步
sum_time += subTime + 2
# 在后序位置对当前节点的情况和子树返回的信息进行处理:
if sum_time > 0 or self.hasApple[root]:
# 子树中发现苹果,或者当前节点是苹果,直接返回,sum_time 已经算上了本节点出入子树的步数
return sum_time
# 以 root 为根的这棵多叉树中不存在苹果,按照定义返回 -1
return -1可视化
算法可视化面板
写在后序位置的代码是最潇洒的,上通父节点(可以通过函数参数获取父节点信息),下通子树(可以通过递归返回值收集子树信息),有少部分难度比较大的题目会同时用到这两个特性。
968. 监控二叉树
968. 监控二叉树 | 力扣 | LeetCode | 🔴
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:

输入:[0,0,null,0,0] 输出:1 解释:如图所示,一台摄像头足以监控所有节点。
示例 2:

输入:[0,0,null,0,null,0,null,null,0] 输出:2 解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
- 给定树的节点数的范围是
[1, 1000]。 - 每个节点的值都是 0。
基本思路
前文 手把手刷二叉树总结篇 说过后序位置的特殊之处,后序位置可以接收到子树的信息,同时也可以通过函数参数接收到父节点传递的信息,这道题就可以比较完美地体现这一特点。
首先我们列举一下一个节点可能存在的几种状态:
该节点不在监控区域内,称为 uncover 状态;该节点在附近节点的监控范围内,称为 cover 状态;该节点自己装了摄像头,称为 set 状态。
如何保证安装的摄像头数量尽可能少呢?显然就是要尽可能分散,让每个摄像头物尽其用。
具体来说就是自底向上安装摄像头,在叶子节点的父节点上安装摄像头,然后每隔两层再安装(因为每个摄像头都可以管三层)。
那么一个节点在什么情况下需要被安装摄像头呢?显然是当这个节点的子节点处于 uncover 的状态的时候必须安装摄像头,以便覆盖子节点。
综上,我们需要利用后序位置自底向上遍历二叉树,同时要利用子节点的状态以及父节点的状态,判断当前节点是否需要安装摄像头。
解法中 setCamera 函数就负责按照最优方式给二叉树安装摄像头,同时返回节点的状态。
详细题解:
解法代码
class Solution:
def minCameraCover(self, root: TreeNode) -> int:
self.res = 0
self.setCamera(root, False)
return self.res
# 定义:输入以 root 为根的二叉树,以最优策略在这棵二叉树上放置摄像头,
# 然后返回 root 节点的情况:
# 返回 -1 代表 root 为空,返回 0 代表 root 未被 cover,
# 返回 1 代表 root 已经被 cover,返回 2 代表 root 上放置了摄像头。
def setCamera(self, root: TreeNode, hasParent: bool) -> int:
if root is None:
return -1
# 获取左右子节点的情况
left = self.setCamera(root.left, True)
right = self.setCamera(root.right, True)
# 根据左右子节点的情况和父节点的情况判断当前节点应该做的事情
if left == -1 and right == -1:
# 当前节点是叶子节点
if hasParent:
# 有父节点的话,让父节点来 cover 自己
return 0
# 没有父节点的话,自己 set 一个摄像头
self.res += 1
return 2
if left == 0 or right == 0:
# 左右子树存在没有被 cover 的
# 必须在当前节点 set 一个摄像头
self.res += 1
return 2
if left == 2 or right == 2:
# 左右子树只要有一个 set 了摄像头
# 当前节点就已经是 cover 状态了
return 1
# 剩下 left == 1 && right == 1 的情况
# 即当前节点的左右子节点都被 cover
if hasParent:
# 如果有父节点的话,可以等父节点 cover 自己
return 0
else:
# 没有父节点,只能自己 set 一个摄像头
self.res += 1
return 2可视化
算法可视化面板
979. 在二叉树中分配硬币
979. 在二叉树中分配硬币 | 力扣 | LeetCode | 🟠
给你一个有 n 个结点的二叉树的根结点 root ,其中树中每个结点 node 都对应有 node.val 枚硬币。整棵树上一共有 n 枚硬币。
在一次移动中,我们可以选择两个相邻的结点,然后将一枚硬币从其中一个结点移动到另一个结点。移动可以是从父结点到子结点,或者从子结点移动到父结点。
返回使每个结点上 只有 一枚硬币所需的 最少 移动次数。
示例 1:

输入:root = [3,0,0] 输出:2 解释:一枚硬币从根结点移动到左子结点,一枚硬币从根结点移动到右子结点。
示例 2:

输入:root = [0,3,0] 输出:3 解释:将两枚硬币从根结点的左子结点移动到根结点(两次移动)。然后,将一枚硬币从根结点移动到右子结点。
提示:
- 树中节点的数目为
n 1 <= n <= 1000 <= Node.val <= n- 所有
Node.val的值之和是n
基本思路
做这道题之前,你应该先做一下 543. 二叉树的直径,并且认真理解 手把手刷二叉树总结篇 中说到的后序遍历的用法。
硬币的移动规则看似很复杂,因为一个节点可能需要移出硬币,也可能移入硬币,还要求移动次数最少,是不是感觉无从下手?
对于这种问题,我们首先要观察规律仔细思考,看看能否对题目进行简化,然后再求解。
首先题目说了整棵树上一共有 n 枚硬币,意思是通过移动,一定是可以做到每个节点有且仅有一枚硬币,不存在无解的情况。
现在的情况是,每个节点有 node.val 个硬币,node.val >= 0,允许我们在相邻节点随意移动硬币,计算将所有节点配平(只有 1 个硬币)的最少移动次数。
我们可以简单变换一下:允许每个节点的硬币个数为负数,且只允许子节点向父节点移动硬币。
比方说父节点想向子节点移动 1 个硬币,等价于子节点向父节点移动 -1 个硬币;如果一个节点的硬币个数为 -3,那么他就需要向父节点移动 -4 个硬币,才能让自己的硬币个数变成 1。
这样,我们就不用考虑移入和移出的区别了,想要把一个节点的硬币个数变成 1,就要向父节点移动 node.val - 1 个节点。
现在就可以开始二叉树的通用解题思路:假想你现在站在根节点上,你如何知道把整棵树配平所需的最小移动次数?
左子树来跟你汇报,想给你移动 left 个节点;右子树来找你汇报,想给你移动 right 个节点,那么你所在节点向父节点移动的硬币个数就是:
left + right + (node.val - 1)这个过程中移动次数是:
// 让当前这棵树平衡所需的移动次数
Math.abs(left) + Math.abs(right) + (node.val - 1);现在你去看代码就能理解了。
详细题解:
解法代码
class Solution:
def distributeCoins(self, root: TreeNode) -> int:
self.res = 0
self.getRest(root)
return self.res
# 定义:输入一棵二叉树,返回这棵二叉树中多出的硬币个数,返回负数代表缺少硬币
def getRest(self, root: TreeNode) -> int:
if root is None:
return 0
# 计算左右子树多出的硬币个数
left = self.getRest(root.left)
right = self.getRest(root.right)
# 后序位置,计算当前这棵树配平所需的移动次数
self.res += abs(left) + abs(right) + (root.val - 1)
# 实现函数的定义
return left + right + (root.val - 1)可视化
算法可视化面板
1080. 根到叶路径上的不足节点
1080. 根到叶路径上的不足节点 | 力扣 | LeetCode | 🟠
给你二叉树的根节点 root 和一个整数 limit ,请你同时删除树中所有 不足节点 ,并返回最终二叉树的根节点。
假如通过节点 node 的每种可能的 “根-叶” 路径上值的总和全都小于给定的 limit,则该节点被称之为 不足节点 ,需要被删除。
叶子节点,就是没有子节点的节点。
示例 1:

输入:root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1 输出:[1,2,3,4,null,null,7,8,9,null,14]
示例 2:

输入:root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22 输出:[5,4,8,11,null,17,4,7,null,null,null,5]
示例 3:

输入:root = [1,2,-3,-5,null,4,null], limit = -1 输出:[1,null,-3,4]
提示:
- 树中节点数目在范围
[1, 5000]内 -105 <= Node.val <= 105-109 <= limit <= 109
基本思路
可以说这道题非常精妙,完美运用前文 手把手刷二叉树总结篇 中说到的前序位置和后序位置的特点:
前序位置可以通过函数参数获取父节点传递来的数据,后序位置可以额外获取子树传递回来的数据。
首先,对于一个叶子节点,它本身就是以自己为根的这棵二叉树的路径,那么这条路径是否小于 limit 的约束是很显然的,如果小于 limit,说明它需要被删除。
然后,对于一个非叶子节点 x,它是否是一个「不足节点」,或者说是否存在一条不满足 limit 约束的路径穿过这个节点,其实可以根据子树推导出来。
如果 x 的左右子节点都被删除,那么就说明 x 的左右子树上的路径都不满足 limit 的约束,也就是说所有穿过 x 的路径都不满足约束,即 x 也应该被删除。
根据上述思路实现代码,即可解决这道题。
详细题解:
解法代码
# 定义:输入一个节点 root,和约束 limit,
# 删除以 root 为根的二叉树中的「不足节点」,返回删除完成后的二叉树根节点
class Solution:
def sufficientSubset(self, root: TreeNode, limit: int) -> TreeNode:
if root is None:
return None
# 前序位置,接收父节点传递的 limit 约束决定叶子结点是否需要被删除
if root.left is None and root.right is None:
if root.val < limit:
# 对于叶子节点,如果低于 limit 说明需要被删除
return None
return root
# 先对左右子树进行删除,接收返回值
left = self.sufficientSubset(root.left, limit - root.val)
right = self.sufficientSubset(root.right, limit - root.val)
# 后序位置,根据子树的删除情况决定自己是否需要被删除
if left is None and right is None:
# 如果左右子树不满足 limit - root.val 的约束,那么就存在经过 root
# 节点的路径不满足约束,也就说明 root 节点是「不足节点」,需要被删掉
return None
root.left = left
root.right = right
return root可视化
算法可视化面板
2049. 统计最高分的节点数目
2049. 统计最高分的节点数目 | 力扣 | LeetCode | 🟠
给你一棵根节点为 0 的 二叉树 ,它总共有 n 个节点,节点编号为 0 到 n - 1 。同时给你一个下标从 0 开始的整数数组 parents 表示这棵树,其中 parents[i] 是节点 i 的父节点。由于节点 0 是根,所以 parents[0] == -1 。
一个子树的 大小 为这个子树内节点的数目。每个节点都有一个与之关联的 分数 。求出某个节点分数的方法是,将这个节点和与它相连的边全部 删除 ,剩余部分是若干个 非空 子树,这个节点的 分数 为所有这些子树 大小的乘积 。
请你返回有 最高得分 节点的 数目 。
示例 1:

输入:parents = [-1,2,0,2,0] 输出:3 解释: - 节点 0 的分数为:3 * 1 = 3 - 节点 1 的分数为:4 = 4 - 节点 2 的分数为:1 * 1 * 2 = 2 - 节点 3 的分数为:4 = 4 - 节点 4 的分数为:4 = 4 最高得分为 4 ,有三个节点得分为 4 (分别是节点 1,3 和 4 )。
示例 2:

输入:parents = [-1,2,0] 输出:2 解释: - 节点 0 的分数为:2 = 2 - 节点 1 的分数为:2 = 2 - 节点 2 的分数为:1 * 1 = 1 最高分数为 2 ,有两个节点分数为 2 (分别为节点 0 和 1 )。
提示:
n == parents.length2 <= n <= 105parents[0] == -1- 对于
i != 0,有0 <= parents[i] <= n - 1 parents表示一棵二叉树。
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维,而且要用到后序位置的妙用。
在做这道题之前,建议你先去看下我给 1339. 分裂二叉树的最大乘积 写的思路和解法代码,然后立马就知道这道题的思路了。
简单说,一个节点的 分数 = 左子树节点个数 x 右子树节点个数 x 除自己外其他节点个数。
只要写个 countNode 函数,在后序位置可以得到左右子树的节点个数 leftCount 和 rightCount,然后除自己外其他节点个数 otherCount 就等于总的节点个数 n 减掉左右子树的节点个数再减掉当前节点,最后求个乘积就能算出当前节点的「分数」了。
当然,这道题还有个难点就是:题目给的 parents 数组不是我们经常见到的二叉树形式。
但问题不大,我们可以把 parents 数组转化成类似 图论基础 中讲到的邻接表结构,然后就可以像操作常规二叉树一样写算法了。
详细题解:
解法代码
class Solution:
# 用邻接表表示的一棵二叉树
def __init__(self):
self.tree = None
self.scoreToCount = {}
def countHighestScoreNodes(self, parents):
self.tree = self.buildTree(parents)
self.countNode(0)
# 计算最大分数出现的次数
maxScore = 0
for score in self.scoreToCount.keys():
maxScore = max(maxScore, score)
return self.scoreToCount[maxScore]
# 计算二叉树中的节点个数
def countNode(self, root):
if root == -1:
return 0
# 二叉树中节点总数
n = len(self.tree)
leftCount = self.countNode(self.tree[root][0])
rightCount = self.countNode(self.tree[root][1])
# 后序位置,计算每个节点的「分数」
otherCount = n - leftCount - rightCount - 1
# 注意,这里要把 int 转化成 long,否则会产生溢出!!!
score = max(leftCount, 1) * max(rightCount, 1) * max(otherCount, 1)
# 给分数 score 计数
if score in self.scoreToCount:
self.scoreToCount[score] += 1
else:
self.scoreToCount[score] = 1
return leftCount + rightCount + 1
# 将 parents 数组转化成常规二叉树(邻接表形式)
def buildTree(self, parents):
n = len(parents)
# 表节点 x 的左子节点为 tree[x][0],节点 x 的右子节点为 tree[x][1]
# 若 tree[x][0] 或 tree[x][1] 等于 -1 则代表空指针
tree = [[-1, -1] for _ in range(n)]
# 根据 parents 数组构建二叉树(跳过 parents[0] 根节点)
for i in range(1, n):
parent_i = parents[i]
if tree[parent_i][0] == -1:
tree[parent_i][0] = i
else:
tree[parent_i][1] = i
return tree可视化
算法可视化面板
【练习】运用层序遍历解题 I
二叉树大部分题目都可以用递归的算法解决,但少部分题目用递归比较麻烦的话,我们可以考虑使用层序遍历的方式解决。
102. 二叉树的层序遍历
102. 二叉树的层序遍历 | 力扣 | LeetCode | 🟠
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:

输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1] 输出:[[1]]
示例 3:
输入:root = [] 输出:[]
提示:
- 树中节点数目在范围
[0, 2000]内 -1000 <= Node.val <= 1000
基本思路
这题没啥可说的,二叉树的递归/层序遍历 遍历中介绍了三种层序(BFS)遍历的写法,任写一种都可以。
详细题解:
解法代码
from collections import deque
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
res = []
if root is None:
return res
q = deque()
q.append(root)
# while 循环控制从上向下一层层遍历
while q:
sz = len(q)
# 记录这一层的节点值
level = []
# for 循环控制每一层从左向右遍历
for i in range(sz):
cur = q.popleft()
level.append(cur.val)
if cur.left is not None:
q.append(cur.left)
if cur.right is not None:
q.append(cur.right)
res.append(level)
return res可视化
算法可视化面板
类似题目:
- 103. 二叉树的锯齿形层序遍历 🟠
- 107. 二叉树的层序遍历 II 🟠
- 1161. 最大层内元素和 🟠
- 1302. 层数最深叶子节点的和 🟠
- 1609. 奇偶树 🟠
- 429. N 叉树的层序遍历 🟠
- 637. 二叉树的层平均值 🟢
- 919. 完全二叉树插入器 🟠
- 958. 二叉树的完全性检验 🟠
- 剑指 Offer 32 - I. 从上到下打印二叉树 🟠
- 剑指 Offer 32 - II. 从上到下打印二叉树 II 🟢
- 剑指 Offer 32 - III. 从上到下打印二叉树 III 🟠
107. 二叉树的层序遍历 II
107. 二叉树的层序遍历 II | 力扣 | LeetCode | 🟠
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
示例 1:

输入:root = [3,9,20,null,null,15,7] 输出:[[15,7],[9,20],[3]]
示例 2:
输入:root = [1] 输出:[[1]]
示例 3:
输入:root = [] 输出:[]
提示:
- 树中节点数目在范围
[0, 2000]内 -1000 <= Node.val <= 1000
基本思路
这题和 102. 二叉树的层序遍历 几乎是一样的,自顶向下的层序遍历反过来就行了。
详细题解:
解法代码
from collections import deque
from typing import List, Optional
class Solution:
def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:
res = deque()
if root is None:
return list(res)
q = deque([root])
# while 循环控制从上向下一层层遍历
while q:
sz = len(q)
# 记录这一层的节点值
level = []
# for 循环控制每一层从左向右遍历
for _ in range(sz):
cur = q.popleft()
level.append(cur.val)
if cur.left:
q.append(cur.left)
if cur.right:
q.append(cur.right)
# 把每一层添加到头部,就是自底向上的层序遍历。
res.appendleft(level)
return list(res)可视化
算法可视化面板
103. 二叉树的锯齿形层序遍历
103. 二叉树的锯齿形层序遍历 | 力扣 | LeetCode | 🟠
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
示例 1:

输入:root = [3,9,20,null,null,15,7] 输出:[[3],[20,9],[15,7]]
示例 2:
输入:root = [1] 输出:[[1]]
示例 3:
输入:root = [] 输出:[]
提示:
- 树中节点数目在范围
[0, 2000]内 -100 <= Node.val <= 100
基本思路
这题和 102. 二叉树的层序遍历 几乎是一样的,只要用一个布尔变量 flag 控制遍历方向即可。
详细题解:
解法代码
from collections import deque
class Solution:
def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]:
res = []
if root is None:
return res
q = deque([root])
# 为 true 时向右,false 时向左
flag = True
# while 循环控制从上向下一层层遍历
while q:
sz = len(q)
# 记录这一层的节点值
level = deque()
# for 循环控制每一层从左向右遍历
for i in range(sz):
cur = q.popleft()
# 实现 z 字形遍历
if flag:
level.append(cur.val)
else:
level.appendleft(cur.val)
if cur.left:
q.append(cur.left)
if cur.right:
q.append(cur.right)
# 切换方向
flag = not flag
res.append(list(level))
return res可视化
算法可视化面板
类似题目:
117. 填充每个节点的下一个右侧节点指针 II
117. 填充每个节点的下一个右侧节点指针 II | 力扣 | LeetCode | 🟠
给定一个二叉树:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL 。
初始状态下,所有 next 指针都被设置为 NULL 。
示例 1:

输入:root = [1,2,3,4,5,null,7] 输出:[1,#,2,3,#,4,5,7,#] 解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化输出按层序遍历顺序(由 next 指针连接),'#' 表示每层的末尾。
示例 2:
输入:root = [] 输出:[]
提示:
- 树中的节点数在范围
[0, 6000]内 -100 <= Node.val <= 100
进阶:
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序的隐式栈空间不计入额外空间复杂度。
基本思路
前文 我的算法学习经验 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式。
但这题和 116. 填充每个节点的下一个右侧节点指针 还不一样,输入的不是完全二叉树,所以不好直接用递归。
这题用 BFS 算法 进行层序遍历比较直观,在 for 循环,无非就是想办法遍历所有节点,然后把这个节点和相邻节点连起来罢了。
当然,还有效率更高的方式,就是直接操作指针,不过略有些难懂,暂时不写。
详细题解:
解法代码
class Node:
def __init__(self, val=0, left=None, right=None, next=None):
self.val = val
self.left = left
self.right = right
self.next = next
class Solution:
def connect(self, root: 'Node') -> 'Node':
if root is None:
return None
# 二叉树层序遍历框架
from collections import deque
q = deque([root])
while q:
sz = len(q)
# 遍历一层
pre = None
for i in range(sz):
cur = q.popleft()
# 链接当前层所有节点的 next 指针
if pre is not None:
pre.next = cur
pre = cur
# 将下一层节点装入队列
if cur.left is not None:
q.append(cur.left)
if cur.right is not None:
q.append(cur.right)
return root662. 二叉树最大宽度
662. 二叉树最大宽度 | 力扣 | LeetCode | 🟠
给你一棵二叉树的根节点 root ,返回树的 最大宽度 。
树的 最大宽度 是所有层中最大的 宽度 。
每一层的 宽度 被定义为该层最左和最右的非空节点(即,两个端点)之间的长度。将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度。
题目数据保证答案将会在 32 位 带符号整数范围内。
示例 1:

输入:root = [1,3,2,5,3,null,9] 输出:4 解释:最大宽度出现在树的第 3 层,宽度为 4 (5,3,null,9) 。
示例 2:

输入:root = [1,3,2,5,null,null,9,6,null,7] 输出:7 解释:最大宽度出现在树的第 4 层,宽度为 7 (6,null,null,null,null,null,7) 。
示例 3:

输入:root = [1,3,2,5] 输出:2 解释:最大宽度出现在树的第 2 层,宽度为 2 (3,2) 。
提示:
- 树中节点的数目范围是
[1, 3000] -100 <= Node.val <= 100
基本思路
这道题的解题关键是要给二叉树节点按行进行编号,然后你就可以通过每一行的最左侧节点和最右侧节点的编号推算出这一行的宽度,进而算出最大宽度:
而且,这样编号还可以通过父节点的编号计算得出左右子节点的编号:
假设父节点的编号是 x,左子节点就是 2 * x,右子节点就是 2 * x + 1。
这个特性常见于完全二叉树的题目当中,你可以去看看前文 图文详解二叉堆,实现优先级队列 或者去做一下 1104. 二叉树寻路 这道题。
明白了这个关键点,就可以通过 BFS 或者 DFS 实现解法了,我把两种解法都写出来供你参考。
其中 DFS 的递归解法需要你透彻理解二叉树的遍历顺序,你可以先做一下 199. 二叉树的右视图 这道题。
详细题解:
解法代码
# 层序遍历思路
class Solution:
# 记录节点和对应编号
class Pair:
def __init__(self, node, id):
self.node = node
self.id = id
def widthOfBinaryTree(self, root):
if root is None:
return 0
# 记录最大的宽度
maxWidth = 0
# 标准 BFS 层序遍历算法
q = collections.deque()
q.append(self.Pair(root, 1))
# 从上到下遍历整棵树
while q:
sz = len(q)
start = 0
end = 0
# 从左到右遍历每一行
for i in range(sz):
cur = q.popleft()
curNode = cur.node
curId = cur.id
# 记录当前行第一个和最后一个节点的编号
if i == 0:
start = curId
if i == sz - 1:
end = curId
# 左右子节点入队,同时记录对应节点的编号
if curNode.left is not None:
q.append(self.Pair(curNode.left, curId * 2))
if curNode.right is not None:
q.append(self.Pair(curNode.right, curId * 2 + 1))
# 用当前行的宽度更新最大宽度
maxWidth = max(maxWidth, end - start + 1)
return maxWidth
# 递归遍历思路
class Solution2:
def widthOfBinaryTree(self, root):
if root is None:
return 0
self.firstId = []
self.maxWidth = 1
self.traverse(root, 1, 1)
return self.maxWidth
# 记录最左侧节点的编号
firstId = []
maxWidth = 1
# 二叉树遍历函数
def traverse(self, root, id, depth):
if root is None:
return
if len(self.firstId) == depth - 1:
# 因为代码是先 traverse(root.left) 后 traverse(root.right),
# 所以第一次到达这个深度一定是最左侧的节点,记录其编号
self.firstId.append(id)
else:
# 这个深度的其他节点,负责计算更新当前深度的最大宽度
self.maxWidth = max(self.maxWidth, id - self.firstId[depth - 1] + 1)
self.traverse(root.left, id * 2, depth + 1)
self.traverse(root.right, id * 2 + 1, depth + 1)可视化
算法可视化面板
类似题目:
515. 在每个树行中找最大值
515. 在每个树行中找最大值 | 力扣 | LeetCode | 🟠
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
示例1:

输入: root = [1,3,2,5,3,null,9] 输出: [1,3,9]
示例2:
输入: root = [1,2,3] 输出: [1,3]
提示:
- 二叉树的节点个数的范围是
[0,104] -231 <= Node.val <= 231 - 1
基本思路
首先,这题肯定可以用 BFS 算法解决,for 循环里面判断最大值就行了:
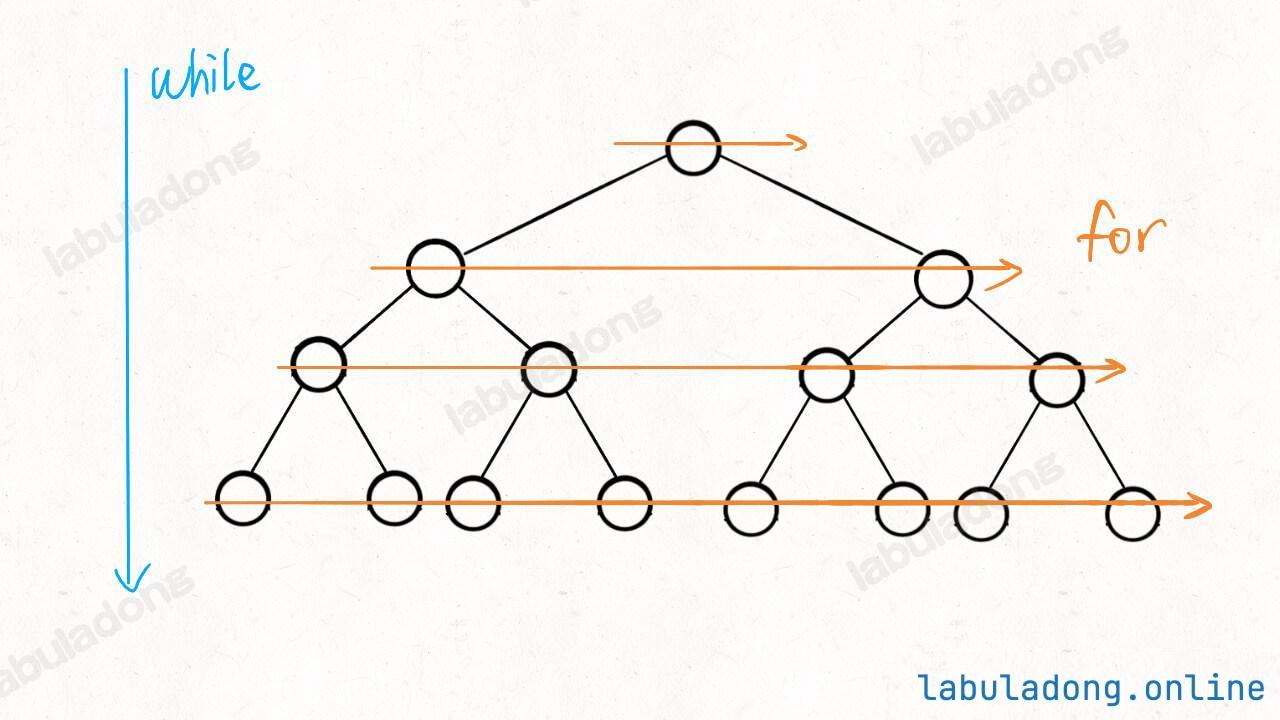
当然,这题也可以用 DFS 来做,前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
遍历的过程中记录对应深度的最大节点值即可。
详细题解:
解法代码
from queue import Queue
from typing import List
class Solution:
def largestValues(self, root: TreeNode) -> List[int]:
res = []
if root is None:
return res
q = Queue()
q.put(root)
# while 循环控制从上向下一层层遍历
while not q.empty():
sz = q.qsize()
# 记录这一层的最大值
levelMax = float('-inf')
# for 循环控制每一层从左向右遍历
for _ in range(sz):
cur = q.get()
levelMax = max(levelMax, cur.val)
if cur.left is not None:
q.put(cur.left)
if cur.right is not None:
q.put(cur.right)
res.append(levelMax)
return res
class Solution_DFS:
# 一定要用 array 存储,因为要用索引随机访问
res = []
def largestValues(self, root: TreeNode) -> List[int]:
if root is None:
return self.res
self.traverse(root, 0)
return self.res
# 遍历二叉树
def traverse(self, root: TreeNode, depth: int) -> None:
if root is None:
return
if len(self.res) <= depth:
self.res.append(root.val)
else:
# 记录当前行的最大值
self.res[depth] = max(self.res[depth], root.val)
self.traverse(root.left, depth + 1)
self.traverse(root.right, depth + 1)可视化
算法可视化面板
类似题目:
637. 二叉树的层平均值
637. 二叉树的层平均值 | 力扣 | LeetCode | 🟢
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。
示例 1:

输入:root = [3,9,20,null,null,15,7] 输出:[3.00000,14.50000,11.00000] 解释:第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。 因此返回 [3, 14.5, 11] 。
示例 2:

输入:root = [3,9,20,15,7] 输出:[3.00000,14.50000,11.00000]
提示:
- 树中节点数量在
[1, 104]范围内 -231 <= Node.val <= 231 - 1
基本思路
标准的二叉树层序遍历,把 102. 层序遍历二叉树 的代码稍微改一改就行了。
详细题解:
解法代码
from collections import deque
from typing import List
class Solution:
def averageOfLevels(self, root: TreeNode) -> List[float]:
res = []
if root is None:
return res
q = deque([root])
while q:
size = len(q)
# 记录当前层所有节点之和
sum = 0
for _ in range(size):
cur = q.popleft()
if cur.left is not None:
q.append(cur.left)
if cur.right is not None:
q.append(cur.right)
sum += cur.val
# 记录当前行的平均值
res.append(sum / size)
return res可视化
算法可视化面板
958. 二叉树的完全性检验
958. 二叉树的完全性检验 | 力扣 | LeetCode | 🟠
给你一棵二叉树的根节点 root ,请你判断这棵树是否是一棵 完全二叉树 。
在一棵 完全二叉树 中,除了最后一层外,所有层都被完全填满,并且最后一层中的所有节点都尽可能靠左。最后一层(第 h 层)中可以包含 1 到 2h 个节点。
示例 1:

输入:root = [1,2,3,4,5,6]
输出:true
解释:最后一层前的每一层都是满的(即,节点值为 {1} 和 {2,3} 的两层),且最后一层中的所有节点({4,5,6})尽可能靠左。
示例 2:

输入:root = [1,2,3,4,5,null,7] 输出:false 解释:值为 7 的节点不满足条件「节点尽可能靠左」。
提示:
- 树中节点数目在范围
[1, 100]内 1 <= Node.val <= 1000
基本思路
这题的关键是对完全二叉树特性的理解,如果按照 BFS 层序遍历的方式遍历完全二叉树,队列最后留下的应该都是空指针:
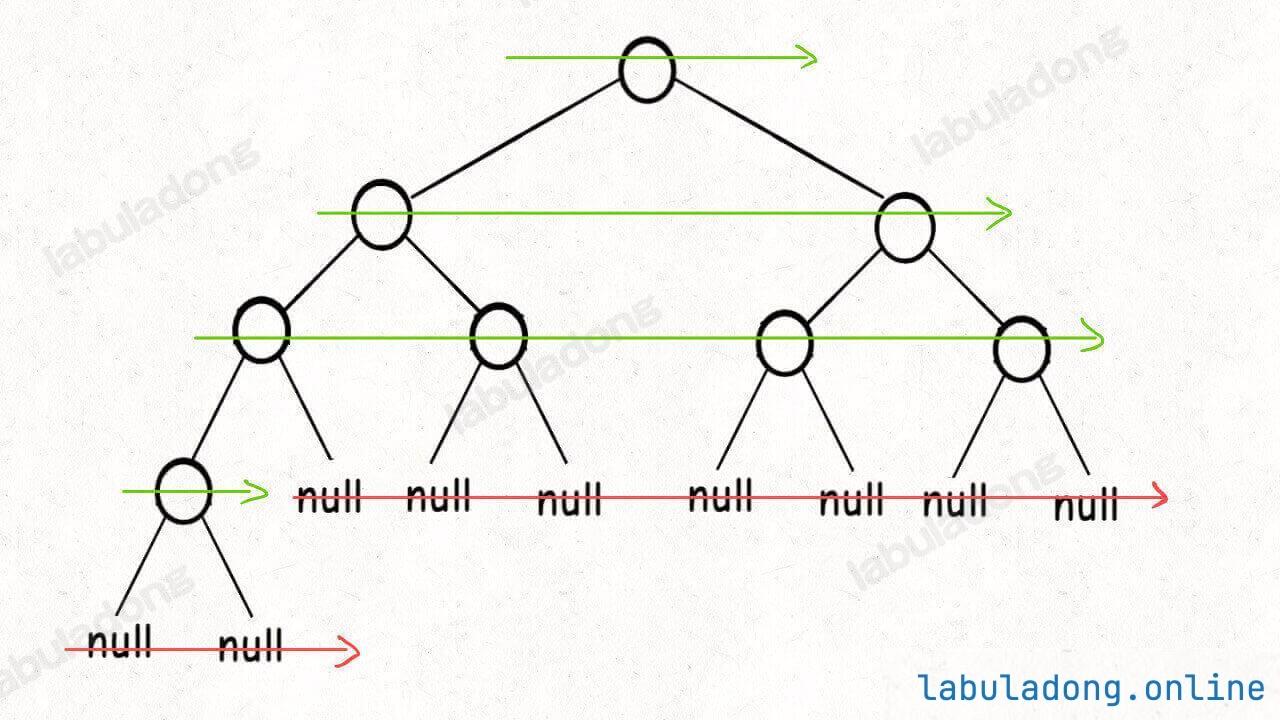
所以可以用 102. 二叉树的层序遍历 给出的层序遍历框架解决这题。
详细题解:
解法代码
from collections import deque
class Solution:
def isCompleteTree(self, root: TreeNode) -> bool:
q = deque([root])
end = False
while q:
sz = len(q)
for i in range(sz):
cur = q.popleft()
if cur is None:
end = True
else:
if end:
return False
q.append(cur.left)
q.append(cur.right)
return True可视化
算法可视化面板
1161. 最大层内元素和
1161. 最大层内元素和 | 力扣 | LeetCode | 🟠
给你一个二叉树的根节点 root。设根节点位于二叉树的第 1 层,而根节点的子节点位于第 2 层,依此类推。
请返回层内元素之和 最大 的那几层(可能只有一层)的层号,并返回其中 最小 的那个。
示例 1:

输入:root = [1,7,0,7,-8,null,null] 输出:2 解释: 第 1 层各元素之和为 1, 第 2 层各元素之和为 7 + 0 = 7, 第 3 层各元素之和为 7 + -8 = -1, 所以我们返回第 2 层的层号,它的层内元素之和最大。
示例 2:
输入:root = [989,null,10250,98693,-89388,null,null,null,-32127] 输出:2
提示:
- 树中的节点数在
[1, 104]范围内 -105 <= Node.val <= 105
基本思路
把 102. 二叉树的层序遍历 给出的层序遍历框架稍微变通即可解决这题。
详细题解:
解法代码
class Solution:
def maxLevelSum(self, root: TreeNode) -> int:
if root is None:
return 0
q = deque([root])
# 记录 BFS 走到的层数
depth = 1
# 记录元素和最大的那一行和最大元素和
res = 0
maxSum = float('-inf')
while q:
sz = len(q)
levelSum = 0
# 遍历这一层
for _ in range(sz):
cur = q.popleft()
levelSum += cur.val
if cur.left is not None:
q.append(cur.left)
if cur.right is not None:
q.append(cur.right)
if levelSum > maxSum:
# 更新最大元素和
res = depth
maxSum = levelSum
depth += 1
return res可视化
算法可视化面板
1302. 层数最深叶子节点的和
1302. 层数最深叶子节点的和 | 力扣 | LeetCode | 🟠
给你一棵二叉树的根节点 root ,请你返回 层数最深的叶子节点的和 。
示例 1:

输入:root = [1,2,3,4,5,null,6,7,null,null,null,null,8] 输出:15
示例 2:
输入:root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5] 输出:19
提示:
- 树中节点数目在范围
[1, 104]之间。 1 <= Node.val <= 100
基本思路
这题用 DFS 或者 BFS 都可以,我就用 BFS 层序遍历算法吧,层序遍历算法参见 102. 层序遍历二叉树,这题只要把最后一层的节点值累加起来就行了。
详细题解:
解法代码
class Solution:
def deepestLeavesSum(self, root: TreeNode) -> int:
if root is None:
return 0
from collections import deque
q = deque([root])
sum = 0
while q:
sum = 0
sz = len(q)
for _ in range(sz):
cur = q.popleft()
# 累加一层的节点之和
sum += cur.val
if cur.left:
q.append(cur.left)
if cur.right:
q.append(cur.right)
# 现在就是最后一层的节点值和
return sum可视化
算法可视化面板
1609. 奇偶树
1609. 奇偶树 | 力扣 | LeetCode | 🟠
如果一棵二叉树满足下述几个条件,则可以称为 奇偶树 :
- 二叉树根节点所在层下标为
0,根的子节点所在层下标为1,根的孙节点所在层下标为2,依此类推。 - 偶数下标 层上的所有节点的值都是 奇 整数,从左到右按顺序 严格递增
- 奇数下标 层上的所有节点的值都是 偶 整数,从左到右按顺序 严格递减
给你二叉树的根节点,如果二叉树为 奇偶树 ,则返回 true ,否则返回 false 。
示例 1:

输入:root = [1,10,4,3,null,7,9,12,8,6,null,null,2] 输出:true 解释:每一层的节点值分别是: 0 层:[1] 1 层:[10,4] 2 层:[3,7,9] 3 层:[12,8,6,2] 由于 0 层和 2 层上的节点值都是奇数且严格递增,而 1 层和 3 层上的节点值都是偶数且严格递减,因此这是一棵奇偶树。
示例 2:

输入:root = [5,4,2,3,3,7] 输出:false 解释:每一层的节点值分别是: 0 层:[5] 1 层:[4,2] 2 层:[3,3,7] 2 层上的节点值不满足严格递增的条件,所以这不是一棵奇偶树。
示例 3:

输入:root = [5,9,1,3,5,7] 输出:false 解释:1 层上的节点值应为偶数。
示例 4:
输入:root = [1] 输出:true
示例 5:
输入:root = [11,8,6,1,3,9,11,30,20,18,16,12,10,4,2,17] 输出:true
提示:
- 树中节点数在范围
[1, 105]内 1 <= Node.val <= 106
基本思路
这道题主要考察二叉树的层序遍历,你可以先做一下 102. 二叉树的层序遍历 和 103. 二叉树的锯齿形层序遍历 这两道题,然后再做这道题。具体思路可看解法代码的注释。
详细题解:
解法代码
import sys
class Solution:
def isEvenOddTree(self, root: TreeNode) -> bool:
if root is None:
return True
q = deque()
q.append(root)
# 记录奇偶层数
even = True
# while 循环控制从上向下一层层遍历
while q:
sz = len(q)
# 记录前一个节点,便于判断是否递增/递减
prev = -sys.maxsize if even else sys.maxsize
# for 循环控制每一层从左向右遍历
for i in range(sz):
cur = q.popleft()
if even:
# 偶数层
if prev >= cur.val or cur.val % 2 == 0:
return False
else:
# 奇数层
if prev <= cur.val or cur.val % 2 == 1:
return False
prev = cur.val
if cur.left is not None:
q.append(cur.left)
if cur.right is not None:
q.append(cur.right)
# 奇偶层数切换
even = not even
return True可视化
算法可视化面板
919. 完全二叉树插入器
919. 完全二叉树插入器 | 力扣 | LeetCode | 🟠
完全二叉树 是每一层(除最后一层外)都是完全填充(即,节点数达到最大)的,并且所有的节点都尽可能地集中在左侧。
设计一种算法,将一个新节点插入到一个完整的二叉树中,并在插入后保持其完整。
实现 CBTInserter 类:
CBTInserter(TreeNode root)使用头节点为root的给定树初始化该数据结构;CBTInserter.insert(int v)向树中插入一个值为Node.val == val的新节点TreeNode。使树保持完全二叉树的状态,并返回插入节点TreeNode的父节点的值;CBTInserter.get_root()将返回树的头节点。
示例 1:

输入 ["CBTInserter", "insert", "insert", "get_root"] [[[1, 2]], [3], [4], []] 输出 [null, 1, 2, [1, 2, 3, 4]]解释
CBTInserter cBTInserter = new CBTInserter([1, 2]);
cBTInserter.insert(3); // 返回 1
cBTInserter.insert(4); // 返回 2
cBTInserter.get_root(); // 返回 [1, 2, 3, 4]
提示:
- 树中节点数量范围为
[1, 1000] 0 <= Node.val <= 5000root是完全二叉树0 <= val <= 5000- 每个测试用例最多调用
insert和get_root操作104次
基本思路
这道题考察二叉树的层序遍历,你需要先做 102. 二叉树的层序遍历 再做这道题,用队列维护底部可以进行插入的节点即可。
详细题解:
解法代码
from queue import Queue
class CBTInserter:
# 这个队列只记录完全二叉树底部可以进行插入的节点
def __init__(self, root: TreeNode):
self.q = Queue()
self.root = root
# 进行普通的 BFS,目的是找到底部可插入的节点
temp = Queue()
temp.put(root)
while not temp.empty():
cur = temp.get()
if cur.left is not None:
temp.put(cur.left)
if cur.right is not None:
temp.put(cur.right)
if cur.right is None or cur.left is None:
# 找到完全二叉树底部可以进行插入的节点
self.q.put(cur)
def insert(self, val: int) -> int:
node = TreeNode(val)
cur = self.q.queue[0]
# 进行插入
if cur.left is None:
cur.left = node
else:
cur.right = node
self.q.get()
# 新节点的左右节点也是可以插入的
self.q.put(node)
return cur.val
def get_root(self) -> TreeNode:
return self.root可视化
算法可视化面板
872. 叶子相似的树
872. 叶子相似的树 | 力扣 | LeetCode | 🟢
请考虑一棵二叉树上所有的叶子,这些叶子的值按从左到右的顺序排列形成一个 叶值序列 。

举个例子,如上图所示,给定一棵叶值序列为 (6, 7, 4, 9, 8) 的树。
如果有两棵二叉树的叶值序列是相同,那么我们就认为它们是 叶相似 的。
如果给定的两个根结点分别为 root1 和 root2 的树是叶相似的,则返回 true;否则返回 false 。
示例 1:

输入:root1 = [3,5,1,6,2,9,8,null,null,7,4], root2 = [3,5,1,6,7,4,2,null,null,null,null,null,null,9,8] 输出:true
示例 2:

输入:root1 = [1,2,3], root2 = [1,3,2] 输出:false
提示:
- 给定的两棵树结点数在
[1, 200]范围内 - 给定的两棵树上的值在
[0, 200]范围内
基本思路
最简单粗暴的方式就是遍历两个二叉树,把所有叶子节点都取出来,然后一个个对比。稍微有点技巧性的解法就是把递归改成栈迭代的形式。
你看这个 next 方法,它和二叉树的递归遍历框架很像,只不过把递归函数改成了栈操作;它和层序遍历的框架也很像,只不过把队列换成了栈,是不是挺有意思的?这个解法相当于就是用栈模拟了递归,对这棵二叉树进行前序遍历。
详细题解:
解法代码
class Solution:
def leafSimilar(self, root1: TreeNode, root2: TreeNode) -> bool:
it1 = LeafIterator(root1)
it2 = LeafIterator(root2)
# 逐一对比叶子节点
while it1.hasNext() and it2.hasNext():
if it1.next().val != it2.next().val:
return False
# 最后应该都完成遍历
return not it1.hasNext() and not it2.hasNext()
# 一个生成二叉树叶子节点的迭代器
class LeafIterator:
# 模拟递归过程
def __init__(self, root: TreeNode):
self.stk = [root]
def hasNext(self) -> bool:
return len(self.stk) > 0
def next(self) -> TreeNode:
while len(self.stk) > 0:
cur = self.stk.pop()
if cur.left is None and cur.right is None:
# 发现一个叶子结点
return cur
# 先入栈 root.right
if cur.right is not None:
self.stk.append(cur.right)
if cur.left is not None:
self.stk.append(cur.left)
return NoneTip
如果让你从二叉树中的非根节点开始遍历,怎么做呢?其实可以用 map 记录子节点到父节点的映射,从而把二叉树转化成一幅图,然后再编写算法。
863. 二叉树中所有距离为 K 的结点
863. 二叉树中所有距离为 K 的结点 | 力扣 | LeetCode | 🟠
给定一个二叉树(具有根结点 root), 一个目标结点 target ,和一个整数值 k ,返回到目标结点 target 距离为 k 的所有结点的值的数组。
答案可以以 任何顺序 返回。
示例 1:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2 输出:[7,4,1] 解释:所求结点为与目标结点(值为 5)距离为 2 的结点,值分别为 7,4,以及 1
示例 2:
输入: root = [1], target = 1, k = 3 输出: []
提示:
- 节点数在
[1, 500]范围内 0 <= Node.val <= 500Node.val中所有值 不同- 目标结点
target是树上的结点。 0 <= k <= 1000
基本思路
这道题常规的解法就是把二叉树变成一幅「图」,然后在图中用 BFS 算法求距离 target 节点 k 步的所有节点。
关于 BFS 算法的原理,见 BFS 算法核心框架套路。
详细题解:
解法代码
class Solution:
# 记录父节点:node.val -> parentNode
# 题目说了树中所有节点值都是唯一的,所以可以用 node.val 代表 TreeNode
def __init__(self):
self.parent = {}
def distanceK(self, root, target, k):
# 遍历所有节点,记录每个节点的父节点
self.traverse(root, None)
# 开始从 target 节点施放 BFS 算法,找到距离为 k 的节点
from collections import deque
q = deque()
visited = set()
q.append(target)
visited.add(target.val)
# 记录离 target 的距离
dist = 0
res = []
while q:
sz = len(q)
for i in range(sz):
cur = q.popleft()
if dist == k:
# 找到距离起点 target 距离为 k 的节点
res.append(cur.val)
# 向父节点、左右子节点扩散
parentNode = self.parent.get(cur.val)
if parentNode and parentNode.val not in visited:
visited.add(parentNode.val)
q.append(parentNode)
if cur.left and cur.left.val not in visited:
visited.add(cur.left.val)
q.append(cur.left)
if cur.right and cur.right.val not in visited:
visited.add(cur.right.val)
q.append(cur.right)
# 向外扩展一圈
dist += 1
return res
def traverse(self, root, parentNode):
if root is None:
return
self.parent[root.val] = parentNode
# 二叉树递归框架
self.traverse(root.left, root)
self.traverse(root.right, root)可视化
算法可视化面板
类似题目:
【练习】二叉搜索树经典例题 I
99. 恢复二叉搜索树
99. 恢复二叉搜索树 | 力扣 | LeetCode | 🟠
给你二叉搜索树的根节点 root ,该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树 。
示例 1:

输入:root = [1,3,null,null,2] 输出:[3,1,null,null,2] 解释:3 不能是 1 的左孩子,因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。
示例 2:

输入:root = [3,1,4,null,null,2] 输出:[2,1,4,null,null,3] 解释:2 不能在 3 的右子树中,因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。
提示:
- 树上节点的数目在范围
[2, 1000]内 -231 <= Node.val <= 231 - 1
进阶:使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用 O(1) 空间的解决方案吗?
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维模式。
得益于二叉搜索树左小右大的特性,一个重要性质是:二叉搜索树的中序遍历结果有序。
题目说有两个节点的值反了,也就是说中序遍历结果不再是有序的,有两个元素的位置反了。
那么我们在中序遍历的时候找到破坏有序性的这两个元素,交换它们即可。
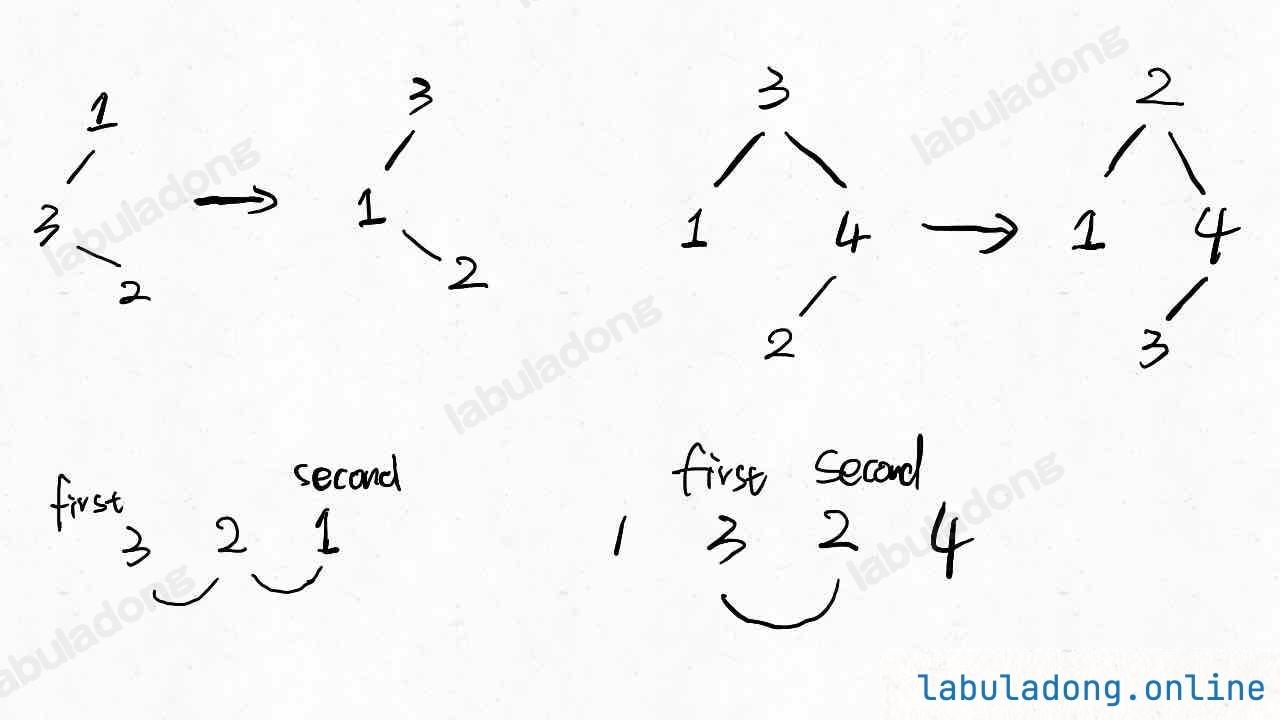
详细题解:
解法代码
class Solution:
# 分别记录这两个被交换的节点
first = None
second = None
# 判断中序遍历的有序性
prev = TreeNode(float('-inf'))
def recoverTree(self, root: TreeNode) -> None:
self.inorderTraverse(root)
temp = self.first.val
self.first.val = self.second.val
self.second.val = temp
def inorderTraverse(self, root: TreeNode) -> None:
if root is None:
return
self.inorderTraverse(root.left)
# 中序代码位置,找出那两个节点
if root.val < self.prev.val:
# root 不符合有序性
if self.first is None:
# 第一个错位节点是 prev
self.first = self.prev
# 第二个错位节点是 root
self.second = root
self.prev = root
self.inorderTraverse(root.right)可视化
算法可视化面板
669. 修剪二叉搜索树
669. 修剪二叉搜索树 | 力扣 | LeetCode | 🟠
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
示例 1:

输入:root = [1,0,2], low = 1, high = 2 输出:[1,null,2]
示例 2:

输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3 输出:[3,2,null,1]
提示:
- 树中节点数在范围
[1, 104]内 0 <= Node.val <= 104- 树中每个节点的值都是 唯一 的
- 题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 104
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维。
明确了递归函数的定义之后进行思考,如果一个节点的值没有落在 [lo, hi] 中,有两种情况:
1、root.val < lo,这种情况下 root 节点本身和 root 的左子树全都是小于 lo 的,都需要被剪掉。
2、root.val > hi,这种情况下 root 节点本身和 root 的右子树全都是大于 hi 的,都需要被剪掉。
详细题解:
解法代码
class Solution:
# 定义:删除 BST 中小于 low 和大于 high 的所有节点,返回结果 BST
def trimBST(self, root: TreeNode, low: int, high: int) -> TreeNode:
if root is None:
return None
if root.val < low:
# 直接返回 root.right
# 等于删除 root 以及 root 的左子树
return self.trimBST(root.right, low, high)
if root.val > high:
# 直接返回 root.left
# 等于删除 root 以及 root 的右子树
return self.trimBST(root.left, low, high)
# 闭区间 [lo, hi] 内的节点什么都不做
root.left = self.trimBST(root.left, low, high)
root.right = self.trimBST(root.right, low, high)
return root可视化
算法可视化面板
类似题目:
671. 二叉树中第二小的节点
671. 二叉树中第二小的节点 | 力扣 | LeetCode | 🟢
给定一个非空特殊的二叉树,每个节点都是正数,并且每个节点的子节点数量只能为 2 或 0。如果一个节点有两个子节点的话,那么该节点的值等于两个子节点中较小的一个。
更正式地说,即 root.val = min(root.left.val, root.right.val) 总成立。
给出这样的一个二叉树,你需要输出所有节点中的 第二小的值 。
如果第二小的值不存在的话,输出 -1 。
示例 1:

输入:root = [2,2,5,null,null,5,7] 输出:5 解释:最小的值是 2 ,第二小的值是 5 。
示例 2:

输入:root = [2,2,2] 输出:-1 解释:最小的值是 2, 但是不存在第二小的值。
提示:
- 树中节点数目在范围
[1, 25]内 1 <= Node.val <= 231 - 1- 对于树中每个节点
root.val == min(root.left.val, root.right.val)
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维。
这题很有意思,按照这棵二叉树的特性,根节点无疑是最小的那个元素,但问题是第二小的那个元素在哪里呢?
如果根节点的左右子节点的值不同,根节点的值就是较小的那个节点(假设是左子节点)的值,那么较大的那个节点(右子节点)的值是不是就一定是第二小的那个元素?
不一定,第二小的值也可能在左子树中,这个节点是左子树中第二小的节点:
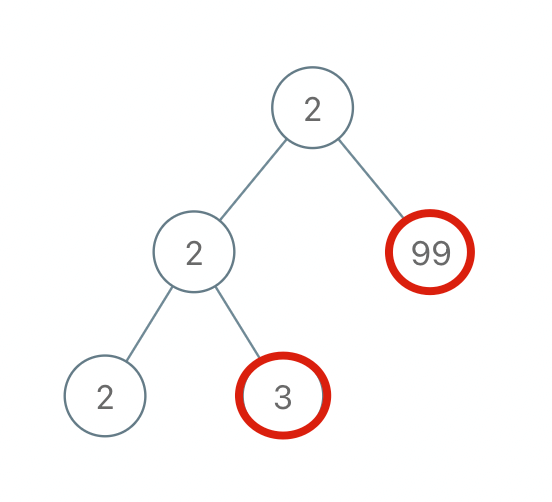
类似的道理,如果根节点的左右子节点相同,那么需要把左右子树的第二小元素计算出来,比较其中较小的元素,作为整棵树的第二小元素:
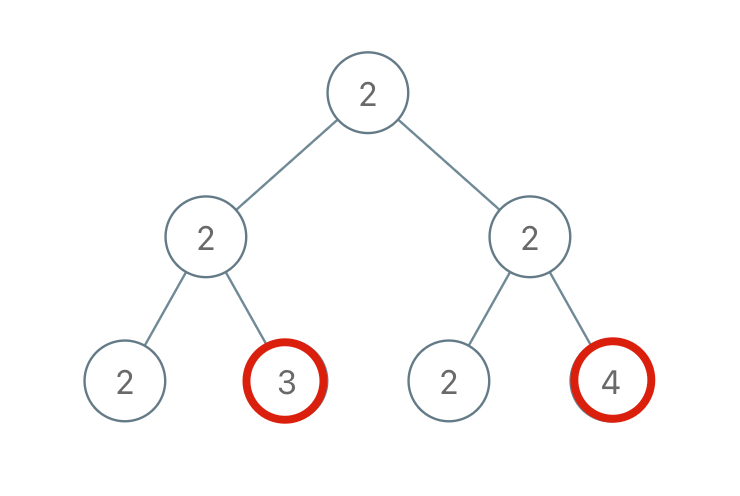
如何计算子树中的第二小元素?函数 findSecondMinimumValue 就是干这个的,递归调用子树即可算出来。
详细题解:
解法代码
class Solution:
# 定义:输入一棵二叉树,返回这棵二叉树中第二小的节点值
def findSecondMinimumValue(self, root: TreeNode) -> int:
if root.left is None and root.right is None:
return -1
# 左右子节点中不同于 root.val 的那个值可能是第二小的值
left, right = root.left.val, root.right.val
# 如果左右子节点都等于 root.val,则去左右子树递归寻找第二小的值
if root.val == root.left.val:
left = self.findSecondMinimumValue(root.left)
if root.val == root.right.val:
right = self.findSecondMinimumValue(root.right)
if left == -1:
return right
if right == -1:
return left
# 如果左右子树都找到一个第二小的值,更小的那个是整棵树的第二小元素
return min(left, right)可视化
算法可视化面板
501. 二叉搜索树中的众数
501. 二叉搜索树中的众数 | 力扣 | LeetCode | 🟢
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
- 结点左子树中所含节点的值 小于等于 当前节点的值
- 结点右子树中所含节点的值 大于等于 当前节点的值
- 左子树和右子树都是二叉搜索树
示例 1:

输入:root = [1,null,2,2] 输出:[2]
示例 2:
输入:root = [0] 输出:[0]
提示:
- 树中节点的数目在范围
[1, 104]内 -105 <= Node.val <= 105
进阶:你可以不使用额外的空间吗?(假设由递归产生的隐式调用栈的开销不被计算在内)
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
BST 的中序遍历有序,在中序遍历的位置做一些判断逻辑和操作有序数组差不多,很容易找出众数。
详细题解:
解法代码
class Solution:
def __init__(self):
self.mode = []
self.prev = None
# 当前元素的重复次数
self.curCount = 0
# 全局的最长相同序列长度
self.maxCount = 0
def findMode(self, root):
# 执行中序遍历
self.traverse(root)
return self.mode
def traverse(self, root):
if root is None:
return
self.traverse(root.left)
# 中序遍历位置
if self.prev is None:
# 初始化
self.curCount = 1
self.maxCount = 1
self.mode.append(root.val)
else:
if root.val == self.prev.val:
# root.val 重复的情况
self.curCount += 1
if self.curCount == self.maxCount:
# root.val 是众数
self.mode.append(root.val)
elif self.curCount > self.maxCount:
# 更新众数
self.mode = []
self.maxCount = self.curCount
self.mode.append(root.val)
else:
# root.val 不重复的情况
self.curCount = 1
if self.curCount == self.maxCount:
self.mode.append(root.val)
# 别忘了更新 prev
self.prev = root
self.traverse(root.right)可视化
算法可视化面板
530. 二叉搜索树的最小绝对差
530. 二叉搜索树的最小绝对差 | 力扣 | LeetCode | 🟢
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。
示例 1:

输入:root = [4,2,6,1,3] 输出:1
示例 2:

输入:root = [1,0,48,null,null,12,49] 输出:1
提示:
- 树中节点的数目范围是
[2, 104] 0 <= Node.val <= 105
注意:本题与 783 https://leetcode-cn.com/problems/minimum-distance-between-bst-nodes/ 相同
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「遍历」的思维。
记住,看到一棵 BST,你就把它理解是一个有序数组就行了,只是遍历方式不同罢了。所以这道题的思路就很简单,用中序遍历遍历一遍 BST 的所有节点得到有序结果,然后在遍历过程中计算最小差值即可。
详细题解:
解法代码
class Solution:
def __init__(self):
self.prev = None
self.res = float('inf')
def getMinimumDifference(self, root: TreeNode) -> int:
self.traverse(root)
return self.res
# 遍历函数
def traverse(self, root: TreeNode):
if root is None:
return
self.traverse(root.left)
# 中序遍历位置
if self.prev is not None:
self.res = min(self.res, root.val - self.prev.val)
self.prev = root
self.traverse(root.right)可视化
算法可视化面板
类似题目:
653. 两数之和 IV - 输入 BST
653. 两数之和 IV - 输入二叉搜索树 | 力扣 | LeetCode | 🟢
给定一个二叉搜索树 root 和一个目标结果 k,如果二叉搜索树中存在两个元素且它们的和等于给定的目标结果,则返回 true。
示例 1:

输入: root = [5,3,6,2,4,null,7], k = 9 输出: true
示例 2:

输入: root = [5,3,6,2,4,null,7], k = 28 输出: false
提示:
- 二叉树的节点个数的范围是
[1, 104]. -104 <= Node.val <= 104- 题目数据保证,输入的
root是一棵 有效 的二叉搜索树 -105 <= k <= 105
基本思路
这道题的思路蛮多的,我们就利用 BST 中序遍历有序这个性质外加 一个函数秒杀 nSum 问题 中的双指针思路来解决吧。
详细题解:
解法代码
class Solution:
def findTarget(self, root: TreeNode, k: int) -> bool:
# 转化成有序数组
arr = self.traverse(root)
# 有序数组中的左右双指针
i, j = 0, len(arr) - 1
while i < j:
sum_val = arr[i] + arr[j]
if sum_val < k:
# sum 调大一点
i += 1
elif sum_val > k:
# sum 调小一点
j -= 1
else:
return True
return False
# 返回中序遍历结果
def traverse(self, root: TreeNode) -> List[int]:
res = []
if root is None:
return res
res.extend(self.traverse(root.left))
res.append(root.val)
res.extend(self.traverse(root.right))
return res可视化
算法可视化面板
类似题目:
1008. 前序遍历构造二叉搜索树
1008. 前序遍历构造二叉搜索树 | 力扣 | LeetCode | 🟠
给定一个整数数组,它表示BST(即 二叉搜索树 )的 先序遍历 ,构造树并返回其根。
保证 对于给定的测试用例,总是有可能找到具有给定需求的二叉搜索树。
二叉搜索树 是一棵二叉树,其中每个节点, Node.left 的任何后代的值 严格小于 Node.val , Node.right 的任何后代的值 严格大于 Node.val。
二叉树的 前序遍历 首先显示节点的值,然后遍历Node.left,最后遍历Node.right。
示例 1:

输入:preorder = [8,5,1,7,10,12] 输出:[8,5,10,1,7,null,12]
示例 2:
输入: preorder = [1,3] 输出: [1,null,3]
提示:
1 <= preorder.length <= 1001 <= preorder[i] <= 10^8preorder中的值 互不相同
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维。
前文 二叉树的花式构造 和 二叉树的序列化和反序列化 说过,生成二叉树的题目,无非就是先生成根节点,然后递归生成左右子树,最后把根节点和左右子树连接起来。具体区别在于你如何找到根节点,如何划分左右子树。
根据前序遍历的特点是,根节点在第一位,后面接着左子树和右子树;BST 的特点,左子树都比根节点的值小,右子树都比根节点的值大。
所以如何找到根节点?前序遍历的第一个就是根节点。
如何找到左右子树?比根节点小的就是左子树的节点,比根节点大的就是右子树的节点。
最后,确定清楚 build 函数的定义,利用这个函数递归生成 BST 即可。
详细题解:
解法代码
class Solution:
def bstFromPreorder(self, preorder):
return self.build(preorder, 0, len(preorder) - 1)
# 定义:将 preorder[start..end] 区间内的元素生成 BST,并返回根节点
def build(self, preorder, start, end):
if start > end:
return None
# 根据前序遍历的特点,根节点在第一位,后面接着左子树和右子树
rootVal = preorder[start]
root = TreeNode(rootVal)
# 根据 BST 的特点,左子树都比根节点的值小,右子树都比根节点的值大
# p 就是左右子树的分界点
p = start + 1
while p <= end and preorder[p] < rootVal:
p += 1
# [start+1, p-1] 区间内是左子树元素
root.left = self.build(preorder, start + 1, p - 1)
# [p, end] 区间内是右子树元素
root.right = self.build(preorder, p, end)
return root可视化
算法可视化面板
类似题目:
108. 将有序数组转换为二叉搜索树
108. 将有序数组转换为二叉搜索树 | 力扣 | LeetCode | 🟢
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 平衡 二叉搜索树。
示例 1:

输入:nums = [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:

输入:nums = [1,3] 输出:[3,1] 解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums按 严格递增 顺序排列
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维模式。
二叉树的构建问题遵循固定的套路,构造整棵树可以分解成:先构造根节点,然后构建左右子树。
一个有序数组对于 BST 来说就是中序遍历结果,根节点在数组中心,数组左侧是左子树元素,右侧是右子树元素。
详细题解:
解法代码
class Solution:
def sortedArrayToBST(self, nums):
return self.build(nums, 0, len(nums) - 1)
# 将闭区间 [left, right] 中的元素转化成 BST,返回根节点
def build(self, nums, left, right):
if left > right:
# 区间为空
return None
# 构造根节点
# BST 节点左小右大,中间的元素就是根节点
mid = (left + right) // 2
root = TreeNode(nums[mid])
# 递归构建左子树
root.left = self.build(nums, left, mid - 1)
# 递归构造右子树
root.right = self.build(nums, mid + 1, right)
return root可视化
算法可视化面板
类似题目:
1382. 将二叉搜索树变平衡
1382. 将二叉搜索树变平衡 | 力扣 | LeetCode | 🟠
给你一棵二叉搜索树,请你返回一棵 平衡后 的二叉搜索树,新生成的树应该与原来的树有着相同的节点值。如果有多种构造方法,请你返回任意一种。
如果一棵二叉搜索树中,每个节点的两棵子树高度差不超过 1 ,我们就称这棵二叉搜索树是 平衡的 。
示例 1:

输入:root = [1,null,2,null,3,null,4,null,null] 输出:[2,1,3,null,null,null,4] 解释:这不是唯一的正确答案,[3,1,4,null,2,null,null] 也是一个可行的构造方案。
示例 2:

输入: root = [2,1,3] 输出: [2,1,3]
提示:
- 树节点的数目在
[1, 104]范围内。 1 <= Node.val <= 105
基本思路
这题可难可简单,如果要难,就是红黑树左旋右旋那一套,不过真的没必要这么搞。
我们简单点,就是用中序遍历获取 BST 的有序结果,然后用 108. 将有序数组转换为二叉搜索树 的解法代码,将这个有序数组转化成平衡 BST。
详细题解:
解法代码
class Solution:
def balanceBST(self, root: TreeNode) -> TreeNode:
# 中序遍历获取有序数组
nums = self.traverse(root)
# 从有序数组构建 BST
return self.build(nums, 0, len(nums) - 1)
# 返回中序遍历结果
def traverse(self, root: TreeNode) -> list:
res = []
if root is None:
return res
res.extend(self.traverse(root.left))
res.append(root.val)
res.extend(self.traverse(root.right))
return res
# BST 构造函数,见 108. 将有序数组转换为二叉搜索树
def build(self, nums: list, lo: int, hi: int) -> TreeNode:
if lo > hi:
return None
mid = lo + (hi - lo) // 2
root = TreeNode(nums[mid])
root.left = self.build(nums, lo, mid - 1)
root.right = self.build(nums, mid + 1, hi)
return root可视化
算法可视化面板
449. 序列化和反序列化二叉搜索树
449. 序列化和反序列化二叉搜索树 | 力扣 | LeetCode | 🟠
序列化是将数据结构或对象转换为一系列位的过程,以便它可以存储在文件或内存缓冲区中,或通过网络连接链路传输,以便稍后在同一个或另一个计算机环境中重建。
设计一个算法来序列化和反序列化 二叉搜索树 。 对序列化/反序列化算法的工作方式没有限制。 您只需确保二叉搜索树可以序列化为字符串,并且可以将该字符串反序列化为最初的二叉搜索树。
编码的字符串应尽可能紧凑。
示例 1:
输入:root = [2,1,3] 输出:[2,1,3]
示例 2:
输入:root = [] 输出:[]
提示:
- 树中节点数范围是
[0, 104] 0 <= Node.val <= 104- 题目数据 保证 输入的树是一棵二叉搜索树。
基本思路
在做本题之前,你需要先看前文 二叉树的序列化和反序列化的不同方式,然后就可以很容易理解本题的思路了。
二叉树的构造算法通用思路很简单,无非就是构造根节点,然后递归构造左右子树,最后把它们接起来,关键在于如何找到根节点和左右子树的节点,不同的序列化方法,找根节点的方式也不同。
本题当然可以直接复制 297. 二叉树的序列化和反序列化 的代码过来,但是显然没有利用到 BST 左小右大的特性,复杂度会更高。
对比 297 题普通二叉树的序列化,利用 BST 左小右大的特性主要可以避免序列化空指针,利用 min, max 边界来划定一棵子树的边界,从而提升算法效率。
详细题解:
解法代码
class Codec:
# 分隔符,区分每个节点的值
SEP = ","
def serialize(self, root):
sb = []
self._serialize(root, sb)
return ''.join(sb)
def _serialize(self, root, sb):
if root is None:
return
# 前序遍历位置进行序列化
sb.append(str(root.val) + self.SEP)
self._serialize(root.left, sb)
self._serialize(root.right, sb)
def deserialize(self, data):
if not data:
return None
# 转化成前序遍历结果
inorder = collections.deque(int(s) for s in data.split(self.SEP) if s)
return self._deserialize(inorder, float('-inf'), float('inf'))
# 定义:将 nodes 中值在闭区间 [min, max] 的节点构造成一棵 BST
def _deserialize(self, nodes, min_val, max_val):
if not nodes:
return None
# 前序遍历位置进行反序列化
# 前序遍历结果第一个节点是根节点
root_val = nodes[0]
if root_val > max_val or root_val < min_val:
# 超过闭区间 [min, max],则返回空指针
return None
nodes.popleft()
# 生成 root 节点
root = TreeNode(root_val)
# 构建左右子树
# BST 左子树都比根节点小,右子树都比根节点大
root.left = self._deserialize(nodes, min_val, root_val)
root.right = self._deserialize(nodes, root_val, max_val)
return root技巧二
如果输入的不是有序数组,而是有序链表,应该怎么构造 BST 呢?
109. 有序链表转换二叉搜索树
109. 有序链表转换二叉搜索树 | 力扣 | LeetCode | 🟠
给定一个单链表的头节点 head ,其中的元素 按升序排序 ,将其转换为 平衡 二叉搜索树。
示例 1:

输入: head = [-10,-3,0,5,9] 输出: [0,-3,9,-10,null,5] 解释: 一个可能的答案是[0,-3,9,-10,null,5],它表示所示的高度平衡的二叉搜索树。
示例 2:
输入: head = [] 输出: []
提示:
head中的节点数在[0, 2 * 104]范围内-105 <= Node.val <= 105
基本思路
链表和数组相比的一个关键差异是无法通过索引快速访问元素,所以这题有几个思路:
1、把链表转化成数组,然后直接复用 108. 将有序数组转换为二叉搜索树 的解法。
2、稍微改写 108. 将有序数组转换为二叉搜索树 的解法,用 单链表的六大解题套路 说到的双指针方法获取链表的中点,时间复杂度略高一些。
3、如果深刻理解二叉树算法,可以利用中序遍历的特点写出最优化的解法。
我把第 2 和第 3 种解法写一下。
详细题解:
解法代码
class Solution:
# 解法三、通过中序遍历特点写出的解法
def sortedListToBST(self, head: ListNode) -> TreeNode:
def inorderBuild(left: int, right: int) -> TreeNode:
if left > right:
return None
mid = (left + right) // 2
# 构造左子树
leftTree = inorderBuild(left, mid - 1)
# 构造根节点
root = TreeNode(self.cur.val)
self.cur = self.cur.next
# 构造右子树
rightTree = inorderBuild(mid + 1, right)
# 将左右子树接到根节点上
root.left = leftTree
root.right = rightTree
return root
len = 0
p = head
while p:
len += 1
p = p.next
self.cur = head
return inorderBuild(0, len - 1)
# 解法二、通过找链表中点的方式写出的解法
def sortedListToBST_2(self, head: ListNode) -> TreeNode:
def build(begin: ListNode, end: ListNode) -> TreeNode:
if begin == end:
# 因为是左闭右开区间,所以现在已经成空集了
return None
mid = getMid(begin, end)
root = TreeNode(mid.val)
root.left = build(begin, mid)
root.right = build(mid.next, end)
return root
def getMid(begin: ListNode, end: ListNode) -> ListNode:
slow, fast = begin, begin
while fast != end and fast.next != end:
slow = slow.next
fast = fast.next.next
return slow
return build(head, None)可视化
算法可视化面板
Tip
最后还有一些常考的套路题型,记住就好了。
173. 二叉搜索树迭代器
173. 二叉搜索树迭代器 | 力扣 | LeetCode | 🟠
BSTIterator ,表示一个按中序遍历二叉搜索树(BST)的迭代器:BSTIterator(TreeNode root)初始化BSTIterator类的一个对象。BST 的根节点root会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字,且该数字小于 BST 中的任何元素。boolean hasNext()如果向指针右侧遍历存在数字,则返回true;否则返回false。int next()将指针向右移动,然后返回指针处的数字。
注意,指针初始化为一个不存在于 BST 中的数字,所以对 next() 的首次调用将返回 BST 中的最小元素。
你可以假设 next() 调用总是有效的,也就是说,当调用 next() 时,BST 的中序遍历中至少存在一个下一个数字。
示例:

输入 ["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"] [[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []] 输出 [null, 3, 7, true, 9, true, 15, true, 20, false]解释
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next(); // 返回 3
bSTIterator.next(); // 返回 7
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 9
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 15
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 20
bSTIterator.hasNext(); // 返回 False
提示:
- 树中节点的数目在范围
[1, 105]内 0 <= Node.val <= 106- 最多调用
105次hasNext和next操作
进阶:
- 你可以设计一个满足下述条件的解决方案吗?
next()和hasNext()操作均摊时间复杂度为O(1),并使用O(h)内存。其中h是树的高度。
基本思路
利用栈模拟递归对 BST 进行中序遍历可以认为是一种套路题型,你记住就好了,关键在于理解 pushLeftBranch 函数,深刻理解二叉树递归遍历的过程:
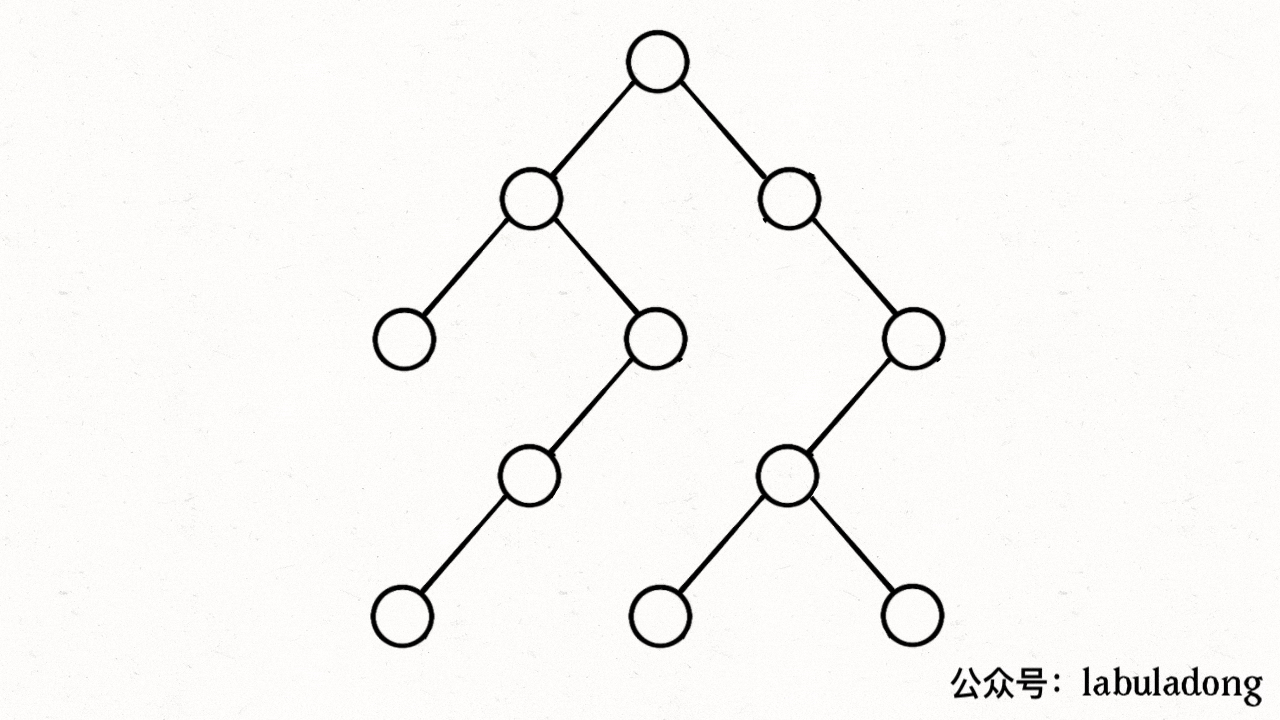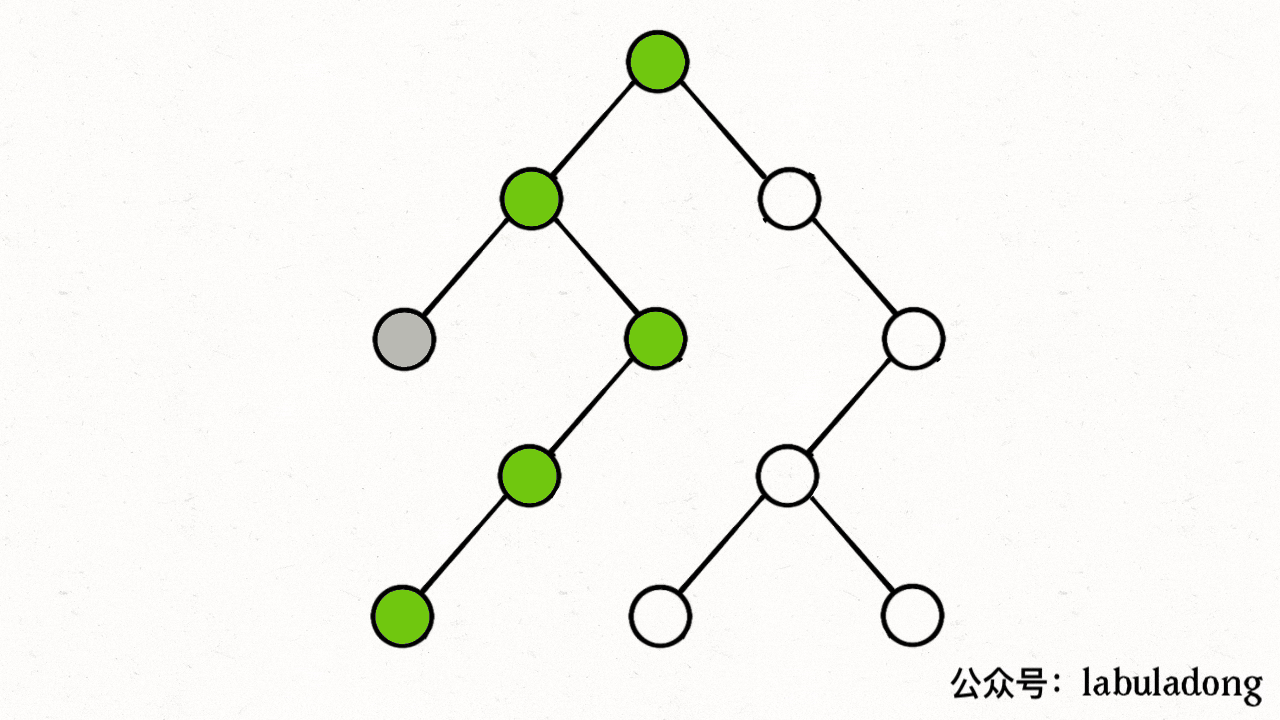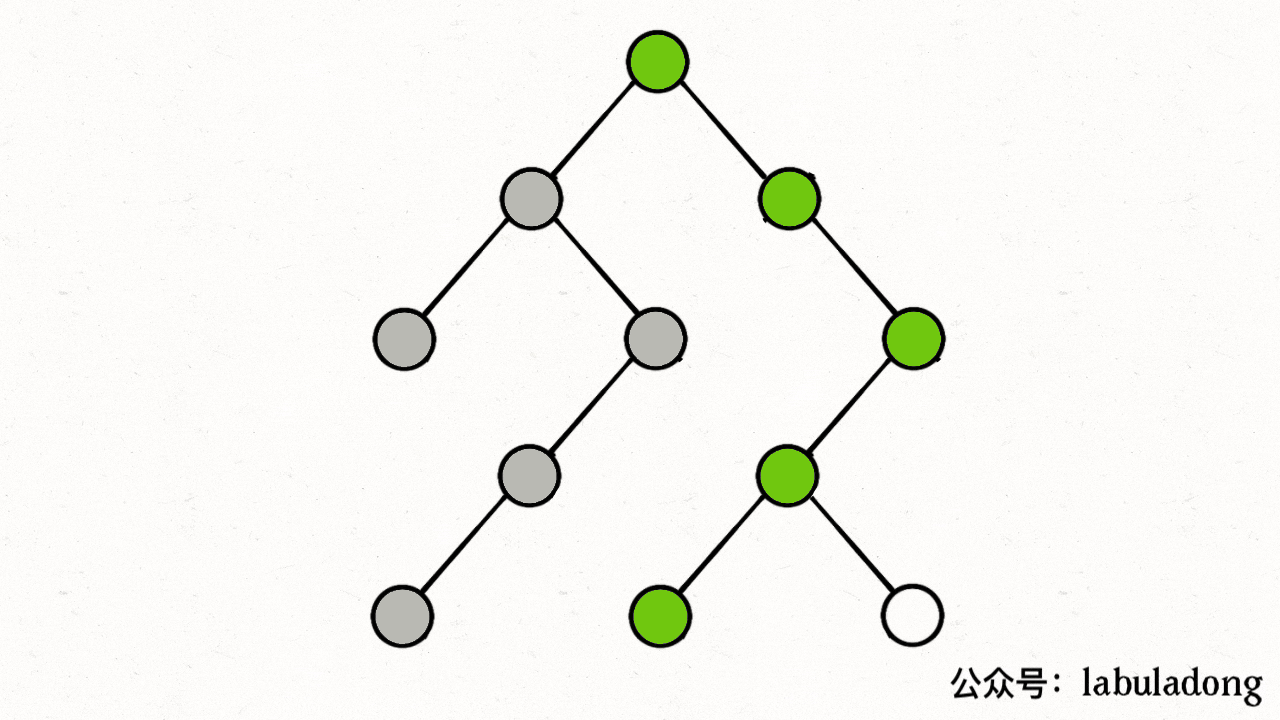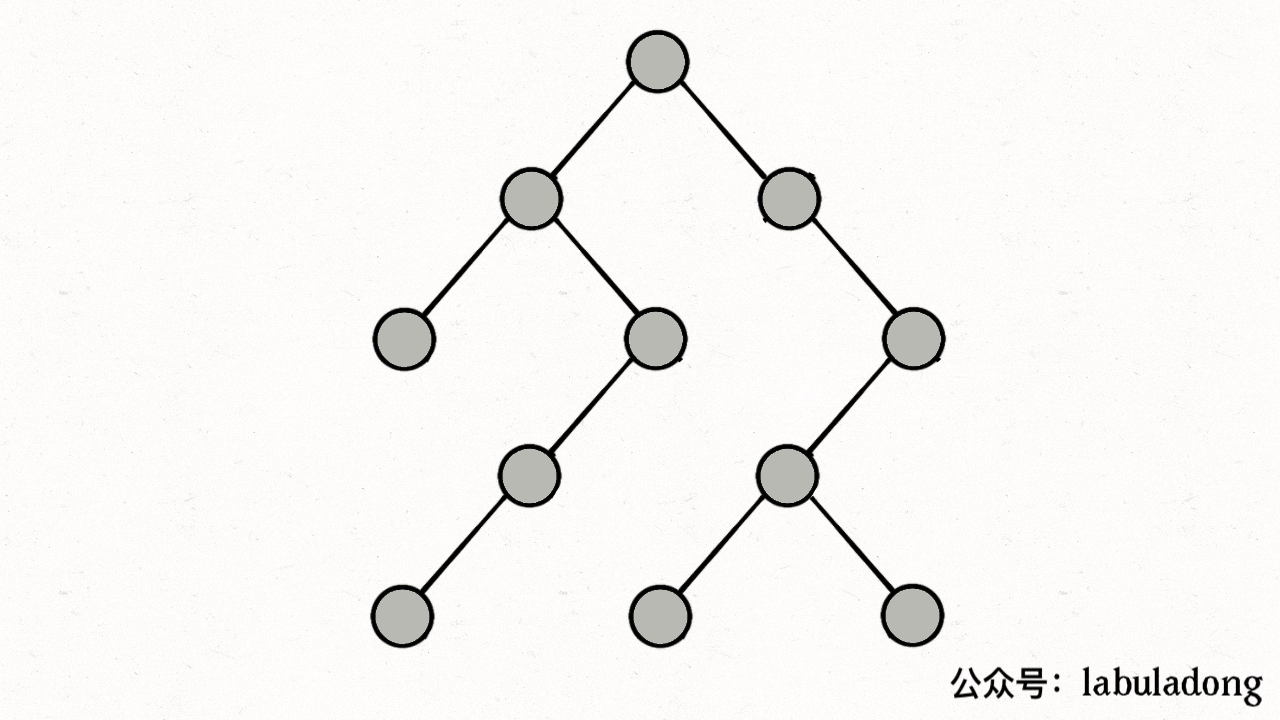
另外,我还总结了一套二叉树各种遍历顺序通用的递归转迭代代码框架,详见 二叉树通用迭代框架。
详细题解:
解法代码
class BSTIterator:
# 模拟递归栈
def __init__(self, root: TreeNode):
self.stk = []
self.pushLeftBranch(root)
# 左侧树枝一撸到底
def pushLeftBranch(self, p: TreeNode):
while p is not None:
self.stk.append(p)
p = p.left
def next(self) -> int:
p = self.stk.pop()
self.pushLeftBranch(p.right)
return p.val
def hasNext(self) -> bool:
return len(self.stk) > 0类似题目:
1305. 两棵二叉搜索树中的所有元素
1305. 两棵二叉搜索树中的所有元素 | 力扣 | LeetCode | 🟠
给你 root1 和 root2 这两棵二叉搜索树。请你返回一个列表,其中包含 两棵树 中的所有整数并按 升序 排序。.
示例 1:

输入:root1 = [2,1,4], root2 = [1,0,3] 输出:[0,1,1,2,3,4]
示例 2:

输入:root1 = [1,null,8], root2 = [8,1] 输出:[1,1,8,8]
提示:
- 每棵树的节点数在
[0, 5000]范围内 -105 <= Node.val <= 105
基本思路
你可以直接中序遍历两个 BST 得到两个有序数组,然后把这两个有序数组合并,这个思路简单,但是空间复杂度会高一些。
比较好的办法是用 173. 二叉搜索树迭代器 中实现的 BST 迭代器,然后类似我们解决 21. 合并两个有序链表 中的逻辑操作这两个迭代器,获得合并的有序结果。
详细题解:
解法代码
class Solution:
def getAllElements(self, root1: TreeNode, root2: TreeNode) -> List[int]:
# BST 有序迭代器
t1 = BSTIterator(root1)
t2 = BSTIterator(root2)
res = []
# 类似合并有序链表的算法逻辑
while t1.hasNext() and t2.hasNext():
if t1.peek() > t2.peek():
res.append(t2.next())
else:
res.append(t1.next())
# 如果有一棵 BST 还剩元素,添加到最后
while t1.hasNext():
res.append(t1.next())
while t2.hasNext():
res.append(t2.next())
return res
# BST 有序迭代器
class BSTIterator:
def __init__(self, root: TreeNode):
self.stk = []
self.pushLeftBranch(root)
# 左侧树枝一撸到底
def pushLeftBranch(self, p: TreeNode):
while p:
self.stk.append(p)
p = p.left
def peek(self) -> int:
return self.stk[-1].val
def next(self) -> int:
p = self.stk.pop()
self.pushLeftBranch(p.right)
return p.val
def hasNext(self) -> bool:
return bool(self.stk)


