二叉搜索树心法(构造篇)
本文讲解的例题
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 95. Unique Binary Search Trees II | 95. 不同的二叉搜索树 II | 🟠 |
| 96. Unique Binary Search Trees | 96. 不同的二叉搜索树 | 🟠 |
前置知识
阅读本文前,你需要先学习:
之前写了两篇手把手刷 BST 算法题的文章,第一篇 讲了中序遍历对 BST 的重要意义,第二篇 写了 BST 的基本操作。
本文就来写手把手刷 BST 系列的第三篇,循序渐进地讲两道题,如何计算所有有效 BST。
第一道题是力扣第 96 题「不同的二叉搜索树」:
96. 不同的二叉搜索树 | 力扣
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:

输入:n = 3 输出:5
示例 2:
输入:n = 1 输出:1
提示:
1 <= n <= 19
函数签名如下:
def numTrees(n: int) -> int:这就是一个正宗的穷举问题,那么什么方式能够正确地穷举有效 BST 的数量呢?
我们前文说过,不要小看「穷举」,这是一件看起来简单但是比较有技术含量的事情,问题的关键就是不能数漏,也不能数多,你咋整?
之前 手把手刷二叉树第一期 说过,二叉树算法的关键就在于明确根节点需要做什么,其实 BST 作为一种特殊的二叉树,核心思路也是一样的。
举个例子,比如给算法输入 n = 5,也就是说用 {1,2,3,4,5} 这些数字去构造 BST。
首先,这棵 BST 的根节点总共有几种情况?
显然有 5 种情况对吧,因为每个数字都可以作为根节点。
比如说我们固定 3 作为根节点,这个前提下能有几种不同的 BST 呢?
根据 BST 的特性,根节点的左子树都比根节点的值小,右子树的值都比根节点的值大。
所以如果固定 3 作为根节点,左子树节点就是 {1,2} 的组合,右子树就是 {4,5} 的组合。
左子树的组合数和右子树的组合数乘积就是 3 作为根节点时的 BST 个数。
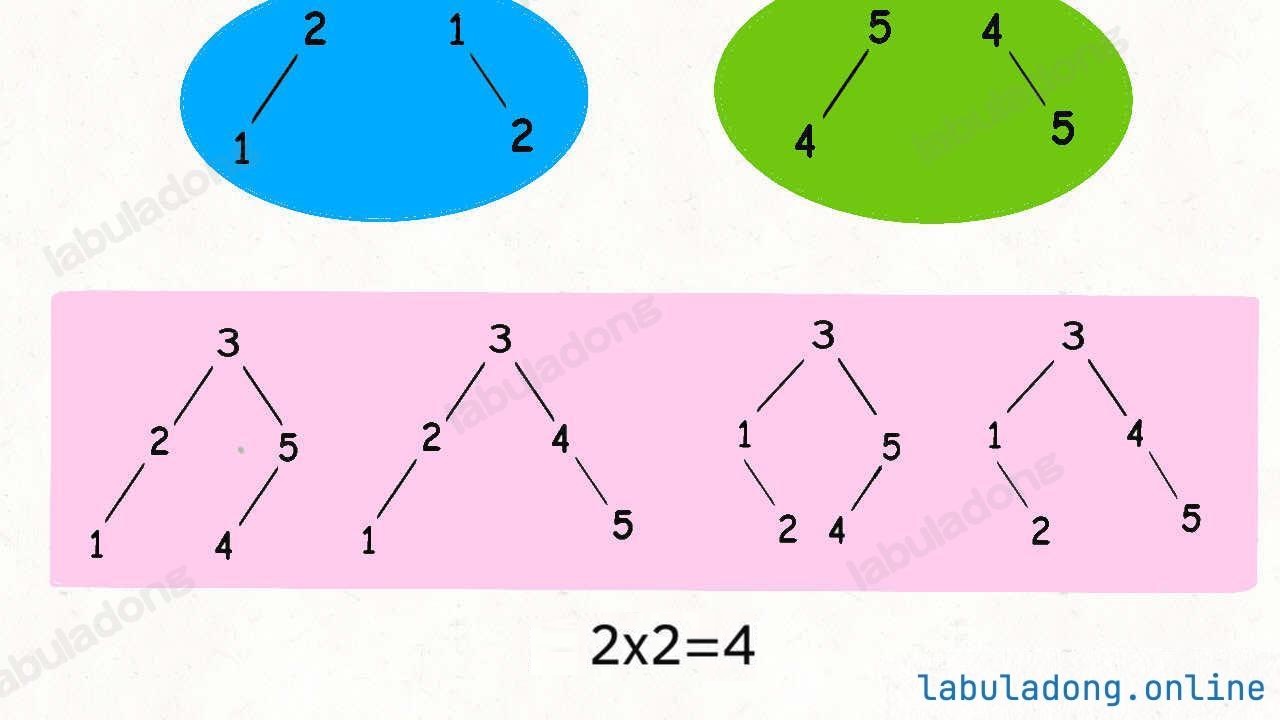
我们这是说了 3 为根节点这一种特殊情况,其实其他的节点也是一样的。
那你可能会问,我们可以一眼看出 {1,2} 和 {4,5} 有几种组合,但是怎么让算法进行计算呢?
其实很简单,只需要递归就行了,我们可以写这样一个函数:
# 定义:闭区间 [lo, hi] 的数字能组成 count(lo, hi) 种 BST
def count(lo: int, hi: int) -> int:根据这个函数的定义,结合刚才的分析,可以写出代码:
class Solution:
def numTrees(self, n: int) -> int:
# 计算闭区间 [1, n] 组成的 BST 个数
return self.count(1, n)
# 计算闭区间 [lo, hi] 组成的 BST 个数
def count(self, lo: int, hi: int) -> int:
# base case
if lo > hi:
return 1
res = 0
for i in range(lo, hi+1):
# i 的值作为根节点 root
left = self.count(lo, i - 1)
right = self.count(i + 1, hi)
# 左右子树的组合数乘积是 BST 的总数
res += left * right
return res注意 base case,显然当 lo > hi 闭区间 [lo, hi] 肯定是个空区间,也就对应着空节点 null,虽然是空节点,但是也是一种情况,所以要返回 1 而不能返回 0。
这样,题目的要求已经实现了,但是时间复杂度非常高,肯定存在重叠子问题。
前文动态规划相关的问题多次讲过消除重叠子问题的方法,无非就是加一个备忘录:
class Solution:
# 备忘录
def __init__(self):
self.memo = []
def numTrees(self, n: int) -> int:
# 备忘录的值初始化为 0
self.memo = [[0] * (n + 1) for _ in range(n + 1)]
return self.count(1, n)
# 定义:返回 [lo, hi] 范围内构造的不同 BST 的数量
def count(self, lo: int, hi: int) -> int:
if lo >= hi:
return 1
# 查备忘录
if self.memo[lo][hi] != 0:
return self.memo[lo][hi]
res = 0
for mid in range(lo, hi + 1):
left = self.count(lo, mid - 1)
right = self.count(mid + 1, hi)
res += left * right
# 将结果存入备忘录
self.memo[lo][hi] = res
return res算法可视化面板
算法可视化面板
这样,这道题就完全解决了。
那么,如果给一个进阶题目,不止让你计算有几个不同的 BST,而是要你构建出所有有效的 BST,如何实现这个算法呢?
这道题就是力扣第 95 题「不同的二叉搜索树 II」,让你构建所有 BST:
95. 不同的二叉搜索树 II | 力扣 | LeetCode | 🟠
给你一个整数 n ,请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。
示例 1:

输入:n = 3 输出:[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]
示例 2:
输入:n = 1 输出:[[1]]
提示:
1 <= n <= 8
函数签名如下:
List<TreeNode> generateTrees(int n);明白了上道题构造有效 BST 的方法,这道题的思路也是一样的:
1、穷举 root 节点的所有可能。
2、递归构造出左右子树的所有有效 BST。
3、给 root 节点穷举所有左右子树的组合。
我们可以直接看代码:
class Solution:
def generateTrees(self, n: int) -> List[TreeNode]:
if n == 0:
return []
# 构造闭区间 [1, n] 组成的 BST
return self.build(1, n)
# 构造闭区间 [lo, hi] 组成的 BST
def build(self, lo: int, hi: int) -> List[TreeNode]:
res = []
# base case
if lo > hi:
# 这里需要装一个 null 元素,这样才能让下面的两个内层 for 循环都能进入,正确地创建出叶子节点
# 举例来说吧,什么时候会进到这个 if 语句?当你创建叶子节点的时候,对吧。
# 那么如果你这里不加 null,直接返回空列表,那么下面的内层两个 for 循环都无法进入
# 你的那个叶子节点就没有创建出来,看到了吗?所以这里要加一个 null,确保下面能把叶子节点做出来
res.append(None)
return res
# 1、穷举 root 节点的所有可能。
for i in range(lo, hi + 1):
# 2、递归构造出左右子树的所有有效 BST。
leftTree = self.build(lo, i - 1)
rightTree = self.build(i + 1, hi)
# 3、给 root 节点穷举所有左右子树的组合。
for left in leftTree:
for right in rightTree:
# i 作为根节点 root 的值
root = TreeNode(i)
root.left = left
root.right = right
res.append(root)
return res算法可视化面板
算法可视化面板
这样,两道题都解决了。
本文就到这里,更多经典的二叉树习题以及递归思维的训练,请参见二叉树章节中的 递归专项练习
二叉搜索树心法(后序篇)
本文讲解的例题
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 1373. Maximum Sum BST in Binary Tree | 1373. 二叉搜索子树的最大键值和 | 🔴 |
前置知识
阅读本文前,你需要先学习:
本文是承接 二叉树心法(纲领篇) 的第五篇文章,主要讲二叉树后序位置的妙用,复述下前文关于后序遍历的描述:
前序位置的代码只能从函数参数中获取父节点传递来的数据,而后序位置的代码不仅可以获取参数数据,还可以获取到子树通过函数返回值传递回来的数据。
那么换句话说,一旦你发现题目和子树有关,那大概率要给函数设置合理的定义和返回值,在后序位置写代码了。
其实二叉树的题目真的不难,无非就是前中后序遍历框架来回倒嘛,只要你把一个节点该做的事情安排好,剩下的抛给递归框架即可。
但是对于有的题目,不同的遍历顺序时间复杂度不同。尤其是这个后序位置的代码,有时候可以大幅提升算法效率。
我们再看看后序遍历的代码框架:
def traverse(root):
if not root:
return
traverse(root.left)
traverse(root.right)
# 后序代码的位置
# 在这里处理当前节点看这个代码框架,你说什么情况下需要在后序位置写代码呢?
如果当前节点要做的事情需要通过左右子树的计算结果推导出来,就要用到后序遍历。
下面就讲一个经典的算法问题,可以直观地体会到后序位置的妙用。这是力扣第 1373 题「二叉搜索子树的最大键值和」,函数签名如下:
def maxSumBST(root: TreeNode)题目分析
题目会给你输入一棵二叉树,这棵二叉树的子树中可能包含二叉搜索树对吧,请你找到节点之和最大的那棵二叉搜索树,返回它的节点值之和。
二叉搜索树(简写作 BST)的性质详见基础知识章节 二叉树基础,简单说就是「左小右大」,对于每个节点,整棵左子树都比该节点的值小,整棵右子树都比该节点的值大。
比如题目给了这个例子:
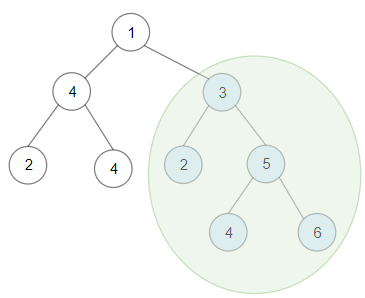
如果输入这棵二叉树,算法应该返回 20,也就是图中绿圈的那棵子树的节点值之和,因为它是一棵 BST,且节点之和最大。
那有的读者可能会问,输入的是一棵普通二叉树,有没有可能其中不存在 BST?
不会的,因为按照 BST 的定义,任何一个单独的节点肯定是 BST,也就是说,再不济,二叉树最下面的叶子节点肯定都是 BST。
比如说如果输入下面这棵二叉树:
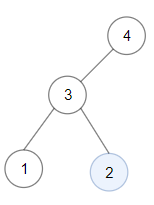
两个叶子节点 1 和 2 就是 BST,比较一下节点之和,算法应该返回 2。
好了,到这里,题目应该解释地很清楚了,下面我们来分析一下这道题应该怎么做。
思路分析
刚才说了,二叉树相关题目最核心的思路是明确当前节点需要做的事情是什么。
那么我们想计算子树中 BST 的最大和,站在当前节点的视角,需要做什么呢?
1、我肯定得知道左右子树是不是合法的 BST,如果下面的这俩儿子有一个不是 BST,以我为根的这棵树肯定不会是 BST,对吧。
2、如果左右子树都是合法的 BST,我得瞅瞅左右子树加上自己还是不是合法的 BST 了。因为按照 BST 的定义,当前节点的值应该大于左子树的最大值,小于右子树的最小值,否则就破坏了 BST 的性质。
3、因为题目要计算最大的节点之和,如果左右子树加上我自己还是一棵合法的 BST,也就是说以我为根的整棵树是一棵 BST,那我需要知道我们这棵 BST 的所有节点值之和是多少,方便和别的 BST 争个高下,对吧。
根据以上三点,站在当前节点的视角,需要知道以下具体信息:
1、左右子树是否是 BST。
2、左子树的最大值和右子树的最小值。
3、左右子树的节点值之和。
只有知道了这几个值,我们才能满足题目的要求,现在可以尝试用伪码写出算法的大致逻辑:
class Solution:
def __init__(self):
# 全局变量,记录 BST 最大节点之和
self.maxSum = 0
def maxSumBST(self, root):
self.traverse(root)
return self.maxSum
# 遍历二叉树
def traverse(self, root):
if root is None:
return
# ******* 前序位置 *******
# 判断左右子树是不是 BST
if self.isBST(root.left) and self.isBST(root.right):
# 计算左子树的最大值和右子树的最小值
leftMax = self.findMax(root.left)
rightMin = self.findMin(root.right)
# 判断以 root 节点为根的树是不是 BST
if root.val > leftMax and root.val < rightMin:
# 如果条件都符合,计算当前 BST 的节点之和
leftSum = self.findSum(root.left)
rightSum = self.findSum(root.right)
rootSum = leftSum + rightSum + root.val
# 计算 BST 节点的最大和
self.maxSum = max(self.maxSum, rootSum)
# **************************
# 二叉树遍历框架,遍历子树节点
self.traverse(root.left)
self.traverse(root.right)
# 计算以 root 为根的二叉树的最大值
def findMax(self, root):
pass
# 计算以 root 为根的二叉树的最小值
def findMin(self, root):
pass
# 计算以 root 为根的二叉树的节点和
def findSum(self, root):
pass
# 判断以 root 为根的二叉树是否是 BST
def isBST(self, root):
pass这个代码逻辑应该是不难理解的,代码在前序遍历的位置把之前的分析都实现了一遍。
其中有四个辅助函数比较简单,我就不具体实现了,其中只有判断合法 BST 的函数稍有技术含量,前文 二叉搜索树操作集锦 写过,这里就不展开了。
稍作分析就会发现,这几个辅助函数都是递归函数,都要遍历输入的二叉树,外加 traverse 函数本身的递归,可以说是递归上加递归,所以这个解法的复杂度是非常高的。
具体来说,每一个辅助方法都是二叉树遍历函数,时间复杂度是 O(N)O(N),而 traverse 遍历框架会在每个节点上都把这些辅助函数调用一遍,所以总的时间复杂度是 O(N2)O(N2)。
但是根据刚才的分析,像 leftMax、rootSum 这些变量又都得算出来,否则无法完成题目的要求。
思路优化
我们希望既算出这些变量,又避免辅助函数带来的额外复杂度,鱼和熊掌全都要,可以做到吗?
其实是可以的,只要把前序遍历变成后序遍历,让 traverse 函数把辅助函数做的事情顺便做掉。
你仔细想想,如果我知道了我的左右子树的最大值,那么把我的值和它们比较一下,就可以推导出以我为根的这整棵二叉树的最大值。根本没必要再遍历一遍所有节点,对吧?求最小节点的值和节点的和也是一样的道理。
这就是我在前文 手把手带你刷二叉树(纲领篇) 所讲的后序遍历位置的妙用。
当然,正如前文所讲,如果要利用函数的返回值,就不建议使用 traverse 这个函数名了,我们想计算最大值、最小值和所有节点之和,不妨叫这个函数 findMaxMinSum 好了。
其他代码不变,我们让 findMaxMinSum 函数做一些计算任务,返回一个大小为 4 的 int 数组,我们暂且称它为 res,其中:
res[0] 记录以 root 为根的二叉树是否是 BST,若为 1 则说明是 BST,若为 0 则说明不是 BST;
res[1] 记录以 root 为根的二叉树所有节点中的最小值;
res[2] 记录以 root 为根的二叉树所有节点中的最大值;
res[3] 记录以 root 为根的二叉树所有节点值之和。
对于当前节点,如果分别对左右子树计算出了这 4 个值,只需要简单的运算,就可以推导出以当前节点为根的二叉树的这 4 个值,避免了重复遍历。
直接看代码实现吧:
class Solution:
def __init__(self):
# 记录 BST 最大节点之和
self.maxSum = 0
def maxSumBST(self, root):
self.findMaxMinSum(root)
return self.maxSum
# 计算以 root 为根的二叉树的最大值、最小值、节点和
def findMaxMinSum(self, root):
# base case
if root is None:
return [1, float('inf'), float('-inf'), 0]
# 递归计算左右子树
left = self.findMaxMinSum(root.left)
right = self.findMaxMinSum(root.right)
# ******* 后序位置 *******
# 通过 left 和 right 推导返回值
# 并且正确更新 maxSum 变量
res = [0, 0, 0, 0]
if left[0] == 1 and right[0] == 1 and root.val > left[2] and root.val < right[1]:
# 以 root 为根的二叉树是 BST
res[0] = 1
# 计算以 root 为根的这棵 BST 的最小值
res[1] = min(left[1], root.val)
# 计算以 root 为根的这棵 BST 的最大值
res[2] = max(right[2], root.val)
# 计算以 root 为根的这棵 BST 所有节点之和
res[3] = left[3] + right[3] + root.val
# 更新全局变量
self.maxSum = max(self.maxSum, res[3])
else:
# 以 root 为根的二叉树不是 BST
res[0] = 0
# 其他的值都没必要计算了,因为用不到
return res这样,这道题就解决了,findMaxMinSum 函数在遍历二叉树的同时顺便把之前辅助函数做的事情都做了,避免了在递归函数中调用递归函数,时间复杂度只有 O(N)。
最后总结
你看,这就是后序遍历的妙用,相对前序遍历的解法,现在的解法不仅效率高,而且代码量少,比较优美。
这个优化属于前文 算法的本质 中提到的「如何聪明的穷举」的范畴。
那可能有读者问,后序遍历这么好,是不是就应该尽可能多用后序遍历?
不是,主要是看题目,看你这个问题适合「遍历」的思路还是「分解问题」的思路。为什么这道题用后序遍历有奇效呢,因为我们需要的这些变量全都可以通过子问题的结果推到出来,适合用「分解问题」的思路求解。
你计算以 root 为根的二叉树的节点之和,是不是可以通过左右子树的和加上 root.val 计算出来?
你计算以 root 为根的二叉树的最大值/最小值,是不是可以通过左右子树的最大值/最小值和 root.val 比较出来?
你判断以 root 为根的二叉树是不是 BST,是不是得先判断左右子树是不是 BST?是不是还得看看左右子树的最大值和最小值?
那么充分利用子问题的答案,当然要比每次都傻乎乎遍历所有节点要高效。
以我的刷题经验,我们要尽可能避免递归函数中调用其他递归函数,如果出现这种情况,大概率是代码实现有瑕疵,可以进行类似本文的优化来避免递归套递归。
本文就到这里,更多经典的二叉树习题以及递归思维的训练,请参见二叉树章节中的 递归专项练习。



