拓展:最近公共祖先系列解题框架
如果说笔试的时候经常遇到各种动归回溯这类稍有难度的题目,那么面试会倾向于一些比较经典的问题,难度不算大,而且也比较实用。
本文就用 Git 引出一个经典的算法问题:最近公共祖先(Lowest Common Ancestor,简称 LCA)。
git pull 这个命令我们经常会用,它默认是使用 merge 方式将远端别人的修改拉到本地;如果带上参数 git pull -r,就会使用 rebase 的方式将远端修改拉到本地。
这二者最直观的区别就是:merge 方式合并的分支会看到很多「分叉」,而 rebase 方式合并的分支就是一条直线。但无论哪种方式,如果存在冲突,Git 都会检测出来并让你手动解决冲突。
那么问题来了,Git 是如何检测两条分支是否存在冲突的呢?
以 rebase 命令为例,比如下图的情况,我站在 dev 分支执行 git rebase master,然后 dev 就会接到 master 分支之上:
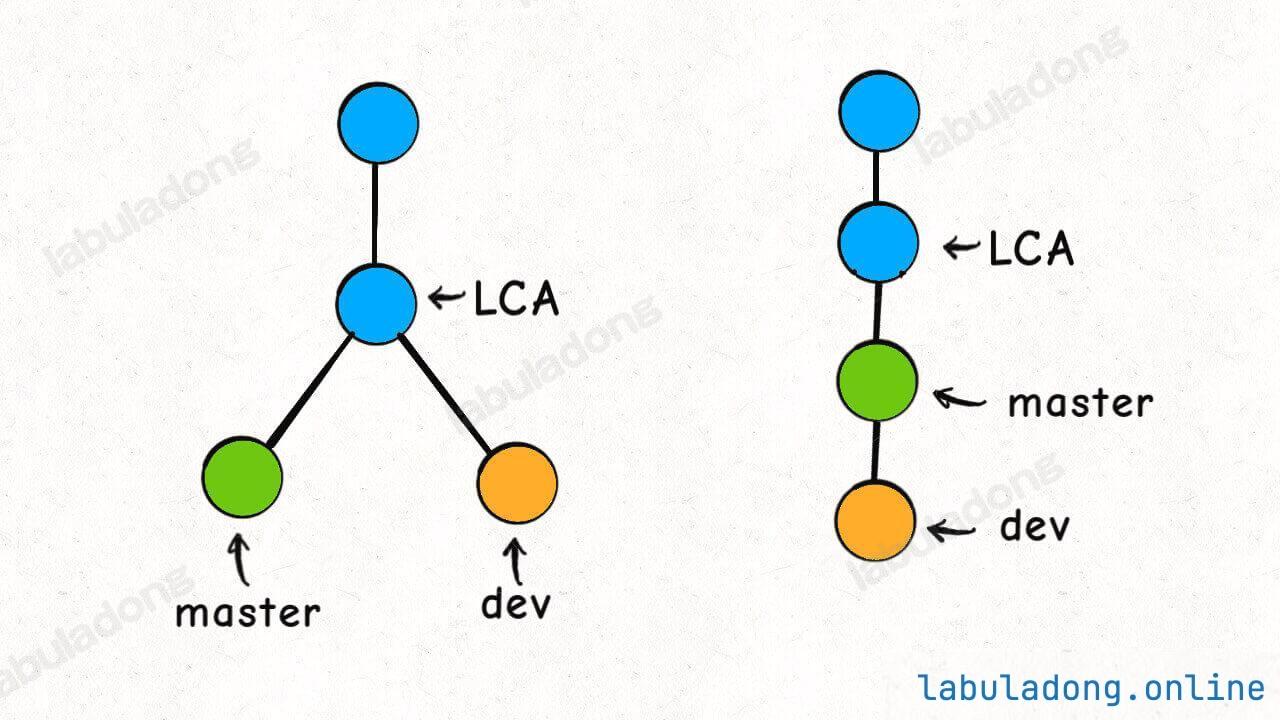
这个过程中,Git 是这么做的:
首先,找到这两条分支的最近公共祖先 LCA,然后从 master 节点开始,重演 LCA 到 dev 几个 commit 的修改,如果这些修改和 LCA 到 master 的 commit 有冲突,就会提示你手动解决冲突,最后的结果就是把 dev 的分支完全接到 master 上面。
那么,Git 是如何找到两条不同分支的最近公共祖先的呢?这就是一个经典的算法问题了,下面我来由浅入深讲一讲。
寻找一个元素
先不管最近公共祖先问题,我请你实现一个简单的算法:
给你输入一棵没有重复元素的二叉树根节点 root 和一个目标值 val,请你写一个函数寻找树中值为 val 的节点。
函数签名如下:
def find(root: TreeNode, val: int) -> TreeNode:这个函数应该很容易实现对吧,比如我这样写代码:
# 定义:在以 root 为根的二叉树中寻找值为 val 的节点
def find(root: TreeNode, val: int) -> TreeNode:
# base case
if not root:
return None
# 看看 root.val 是不是要找的
if root.val == val:
return root
# root 不是目标节点,那就去左子树找
left = find(root.left, val)
if left:
return left
# 左子树找不着,那就去右子树找
right = find(root.right, val)
if right:
return right
# 实在找不到了
return None这段代码应该不用我多解释了,下面的可视化面板展示了这段代码的执行过程,你可以多次点击 这一行,即可展示出函数在二叉树上的搜索过程:
算法可视化面板
下面我将基于这段代码做一些简单的改写,请你分析一下我的改动会造成什么影响。
首先,如果修改一下 return 的位置:
def find(root: TreeNode, val: int) -> TreeNode:
if not root:
return None
# 前序位置
if root.val == val:
return root
# root 不是目标节点,去左右子树寻找
left = find(root.left, val)
right = find(root.right, val)
# 看看哪边找到了
return left if left else right这段代码也可以达到目的,但是实际运行的效率会低一些。
原因也很简单,如果你能够在左子树找到目标节点,还有没有必要去右子树找了?没有必要。但这段代码还是会去右子树找一圈,所以效率相对差一些。
下面的可视化面板展示了这段代码的执行过程,你可以多次点击 这一行,即可展示出函数在二叉树上的搜索过程,对比上面的可视化面板,这个函数会遍历二叉树的所有节点:
算法可视化面板
那么,是不是说这种写法一定会遍历二叉树的所有节点呢?不一定,还有一个特殊情况,即要找的目标节点恰好就是根节点。
因为你是在前序位置判断 if (root.val == val) 的,所以这种特殊情况下函数可以直接结束。
更进一步,我把对 root.val 的判断从前序位置移动到后序位置:
def find(root: TreeNode, val: int) -> TreeNode:
if root is None:
return None
# 先去左右子树寻找
left = find(root.left, val)
right = find(root.right, val)
# 后序位置,看看 root 是不是目标节点
if root.val == val:
return root
# root 不是目标节点,再去看看哪边的子树找到了
return left if left is not None else right这段代码相当于你先去左右子树找,最后才检查 root,依然可以到达目的,但是效率会进一步下降,因为这种写法必然会遍历二叉树的每一个节点。
没办法,你是在后序位置判断,那么就算根节点就是目标节点,你也要去左右子树遍历完所有节点才能判断出来。
下面的可视化面板展示了这段代码的执行过程,你可以多次点击 这一行,即可展示出函数在二叉树上的搜索过程:
算法可视化面板
最后,我再改一下题目,现在不让你找值为 val 的节点,而是寻找值为 val1 或 val2 的节点,函数签名如下:
def find(root: TreeNode, val1: int, val2: int) -> TreeNode:为什么要写这样一个奇怪的 find 函数呢?因为最近公共祖先系列问题的解法都是把这个函数作为框架的。
这和我们第一次实现的 find 函数基本上是一样的,而且你应该知道可以有多种写法,比方说我可以这样写代码:
# 定义:在以 root 为根的二叉树中寻找值为 val1 或 val2 的节点
def find(root, val1, val2):
# base case
if root is None:
return None
# 前序位置,看看 root 是不是目标值
if root.val == val1 or root.val == val2:
return root
# 去左右子树寻找
left = find(root.left, val1, val2)
right = find(root.right, val1, val2)
# 后序位置,已经知道左右子树是否存在目标值
return left if left is not None else right当然,这种写法会有重复遍历的问题,不过先不急着优化,最近公共祖先的一系列算法问题还就得基于这种写法展开。
下面一道一道题目来看,后文我用 LCA(Lowest Common Ancestor)作为最近公共祖先节点的缩写。
236. 二叉树的最近公共祖先
先来看看力扣第 236 题「二叉树的最近公共祖先」:
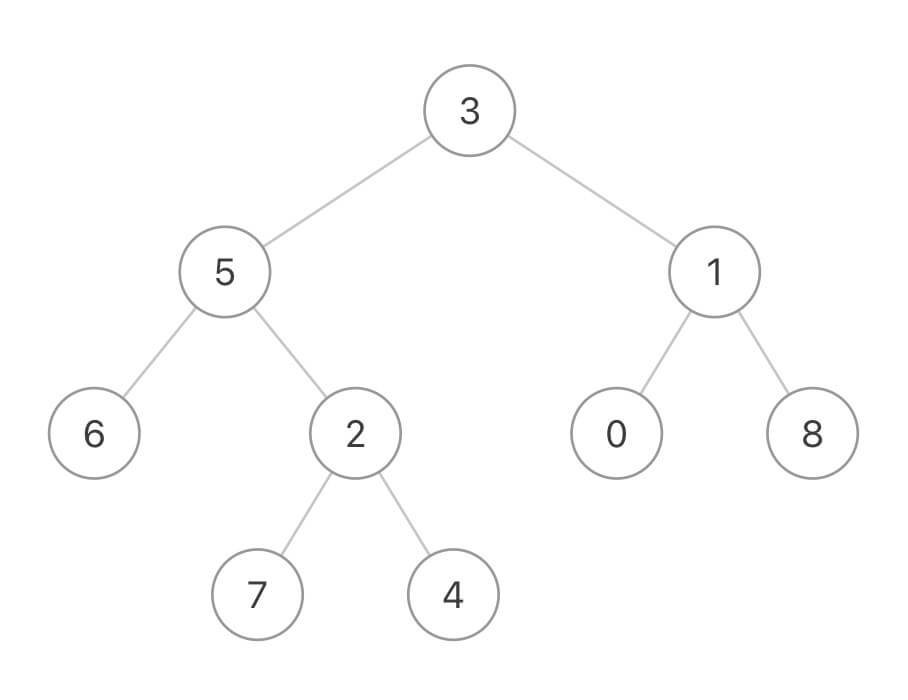
给你输入一棵不含重复值的二叉树,以及存在于树中的两个节点 p 和 q,请你计算 p 和 q 的最近公共祖先节点。
比如输入这样一棵二叉树:
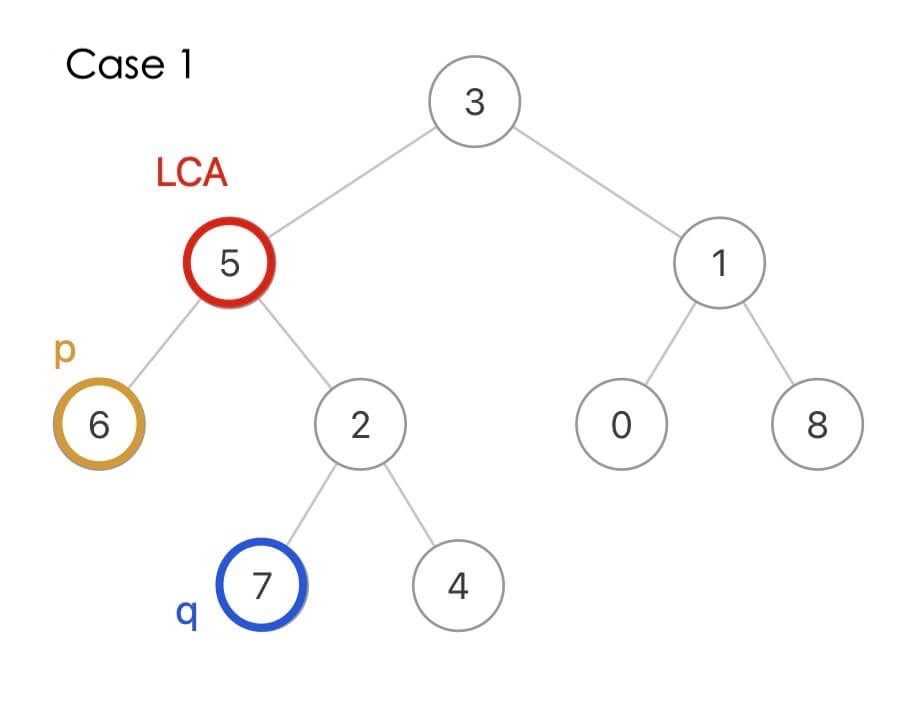
如果 p 是节点 6,q 是节点 7,那么它俩的 LCA 就是节点 5:
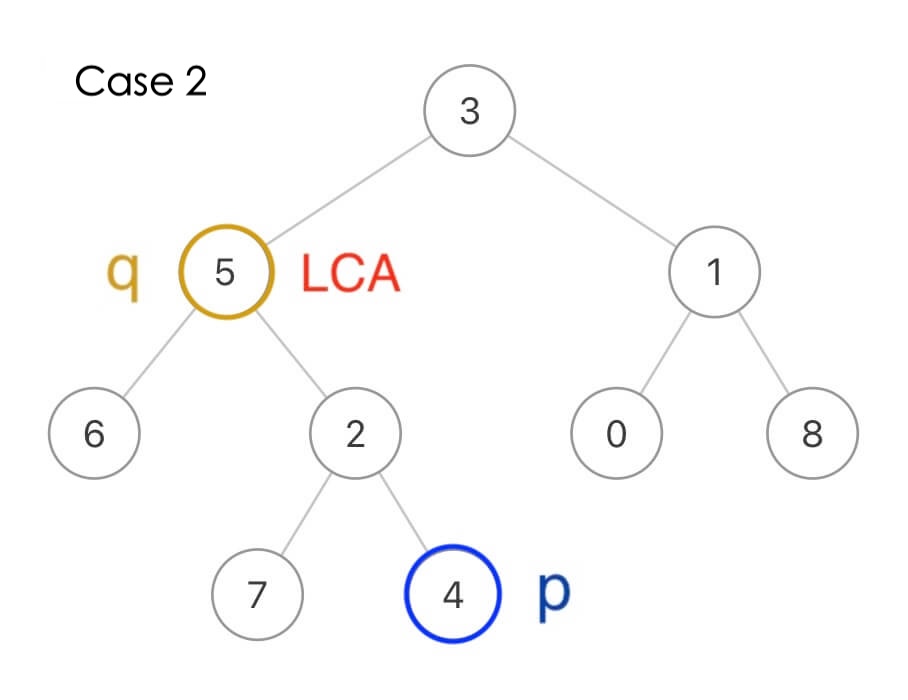
当然,p 和 q 本身也可能是 LCA,比如这种情况 q 本身就是 LCA 节点:
两个节点的最近公共祖先其实就是这两个节点向根节点的「延长线」的交汇点,那么对于任意一个节点,它怎么才能知道自己是不是 p 和 q 的最近公共祖先?
如果一个节点能够在它的左右子树中分别找到 p 和 q,则该节点为 LCA 节点。
这就要用到之前实现的 find 函数了,只需在后序位置添加一个判断逻辑,即可改造成寻找最近公共祖先的解法代码:
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
return self.find(root, p.val, q.val)
# 在二叉树中寻找 val1 和 val2 的最近公共祖先节点
def find(self, root: 'TreeNode', val1: int, val2: int) -> 'TreeNode':
if root is None:
return None
# 前序位置
if root.val == val1 or root.val == val2:
# 如果遇到目标值,直接返回
return root
left = self.find(root.left, val1, val2)
right = self.find(root.right, val1, val2)
# 后序位置,已经知道左右子树是否存在目标值
if left is not None and right is not None:
# 当前节点是 LCA 节点
return root
return left if left is not None else right在 find 函数的后序位置,如果发现 left 和 right 都非空,就说明当前节点是 LCA 节点,即解决了第一种情况:

在 find 函数的前序位置,如果找到一个值为 val1 或 val2 的节点则直接返回,恰好解决了第二种情况:

因为题目说了 p 和 q 一定存在于二叉树中(这点很重要),所以即便我们遇到 q 就直接返回,根本没遍历到 p,也依然可以断定 p 在 q 底下,q 就是 LCA 节点。
下面这个可视化面板展示了这段代码的执行过程,你可以多次点击 这一行,即可展示出函数在二叉树上的搜索过程,你也可以自行修改测试用例玩一玩:
算法可视化面板
结合可视化面板,我们也能发现一个优化的点,就是当我们在左子树找到目标 LCA 节点后,算法并没有结束,而是把右子树又遍历了一遍,这其实是没有必要的。
有前面的铺垫,你是不是想做类似这样的优化?
// root 不是目标节点,那就去左子树找
TreeNode left = find(root.left, val);
if (left != null) {
return left;
}
// 左子树找不着,那就去右子树找
TreeNode right = find(root.right, val);
if (right != null) {
return right;
}不行的,因为我们本来就要同时去左子树和右子树寻找,来判断当前节点是不是 LCA。
如果你非要优化,只能用一个外部变量来辅助判断是否已经找到答案,如果已经找到 LCA,则不再继续遍历二叉树:
class Solution:
def __init__(self):
# 用一个外部变量来记录是否已经找到 LCA 节点
self.lca = None
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
return self.find(root, p.val, q.val)
def find(self, root: 'TreeNode', val1: int, val2: int) -> 'TreeNode':
if root is None:
return None
# 如果已经找到 LCA 节点,直接返回
if self.lca is not None:
return None
if root.val == val1 or root.val == val2:
return root
left = self.find(root.left, val1, val2)
right = self.find(root.right, val1, val2)
if left is not None and right is not None:
# 当前节点是 LCA 节点,记录下来
self.lca = root
return root
return left if left is not None else right这段算法的可视化面板如下,你可以多次点击 这一行,即可展示出函数在二叉树上的搜索过程,找到 LCA 节点后,算法就不再继续遍历右侧的子树了:
算法可视化面板
这样,标准的最近公共祖先问题就解决了,接下来看看这个题目有什么变体。
1676. 二叉树的最近公共祖先 IV
比如力扣第 1676 题「二叉树的最近公共祖先 IV」:
依然给你输入一棵不含重复值的二叉树,但这次不是给你输入 p 和 q 两个节点了,而是给你输入一个包含若干节点的列表 nodes(这些节点都存在于二叉树中),让你算这些节点的最近公共祖先。
函数签名如下:
def lowestCommonAncestor(root: TreeNode, nodes: List[TreeNode]) -> TreeNode:比如还是这棵二叉树:

输入 nodes = [7,4,6],那么函数应该返回节点 5。
看起来怪吓人的,实则解法逻辑是一样的,把刚才的代码逻辑稍加改造即可解决这道题:
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', nodes: 'List[TreeNode]') -> 'TreeNode':
# 将列表转化成哈希集合,便于判断元素是否存在
values = set()
for node in nodes:
values.add(node.val)
return self.find(root, values)
def find(self, root: 'TreeNode', values: 'set') -> 'TreeNode':
if root is None:
return None
# 前序位置
if root.val in values:
return root
left = self.find(root.left, values)
right = self.find(root.right, values)
# 后序位置,已经知道左右子树是否存在目标值
if left is not None and right is not None:
# 当前节点是 LCA 节点
return root
return left if left is not None else right类比一下上一道题应该不难理解这个解法。当找到 LCA 节点后,也可以提前停止算法,这个优化就留给你吧。
需要注意的是,这两道题的题目都明确告诉我们这些节点必定存在于二叉树中,如果没有这个前提条件,就需要修改代码了。
1644. 二叉树的最近公共祖先 II
比如力扣第 1644 题「二叉树的最近公共祖先 II」:
给你输入一棵不含重复值的二叉树的,以及两个节点 p 和 q,如果 p 或 q 不存在于树中,则返回空指针,否则的话返回 p 和 q 的最近公共祖先节点。
在解决标准的最近公共祖先问题时,我们在 find 函数的前序位置有这样一段代码:
// 前序位置
if (root.val == val1 || root.val == val2) {
// 如果遇到目标值,直接返回
return root;
}我也进行了解释,因为 p 和 q 都存在于树中,所以这段代码恰好可以解决最近公共祖先的第二种情况:

但对于这道题来说,p 和 q 不一定存在于树中,所以你不能遇到一个目标值就直接返回,而应该对二叉树进行完全搜索(遍历每一个节点),如果发现 p 或 q 不存在于树中,那么是不存在 LCA 的。
回想我在文章开头分析的几种 find 函数的写法,哪种写法能够对二叉树进行完全搜索来着?
这种:
def find(root: TreeNode, val: int) -> TreeNode:
if root is None:
return None
# 先去左右子树寻找
left = find(root.left, val)
right = find(root.right, val)
# 后序位置,看看 root 是不是目标节点
if root.val == val:
return root
# root 不是目标节点,再去看看哪边的子树找到了
return left if left is not None else right那么解决这道题也是类似的,我们只需要把前序位置的判断逻辑放到后序位置即可:
class Solution:
def __init__(self):
# 用于记录 p 和 q 是否存在于二叉树中
self.foundP = False
self.foundQ = False
def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
res = self.find(root, p.val, q.val)
if not self.foundP or not self.foundQ:
return None
# p 和 q 都存在二叉树中,才有公共祖先
return res
# 在二叉树中寻找 val1 和 val2 的最近公共祖先节点
def find(self, root, val1, val2):
if not root:
return None
left = self.find(root.left, val1, val2)
right = self.find(root.right, val1, val2)
# 后序位置,判断当前节点是不是 LCA 节点
if left and right:
return root
# 后序位置,判断当前节点是不是目标值
if root.val == val1 or root.val == val2:
# 找到了,记录一下
if root.val == val1:
self.foundP = True
if root.val == val2:
self.foundQ = True
return root
return left if left else right这样改造,对二叉树进行完全搜索,同时记录 p 和 q 是否同时存在树中,从而满足题目的要求。
这段算法的可视化面板如下,我构造了一个 q 不在树中的场景,多次点击 即可查看函数搜索二叉树的过程:
算法可视化面板
接下来,我们再变一变,如果让你在二叉搜索树中寻找 p 和 q 的最近公共祖先,应该如何做呢?
235. 二叉搜索树的最近公共祖先
看力扣第 235 题「二叉搜索树的最近公共祖先」:
给你输入一棵不含重复值的二叉搜索树,以及存在于树中的两个节点 p 和 q,请你计算 p 和 q 的最近公共祖先节点。
把之前的解法代码复制过来肯定也可以解决这道题,但没有用到 BST「左小右大」的性质,显然效率不是最高的。
在标准的最近公共祖先问题中,我们要在后序位置通过左右子树的搜索结果来判断当前节点是不是 LCA:
TreeNode left = find(root.left, val1, val2);
TreeNode right = find(root.right, val1, val2);
// 后序位置,判断当前节点是不是 LCA 节点
if (left != null && right != null) {
return root;
}但对于 BST 来说,根本不需要老老实实去遍历子树,由于 BST 左小右大的性质,将当前节点的值与 val1 和 val2 作对比即可判断当前节点是不是 LCA:
假设 val1 < val2,那么 val1 <= root.val <= val2 则说明当前节点就是 LCA;若 root.val 比 val1 还小,则需要去值更大的右子树寻找 LCA;若 root.val 比 val2 还大,则需要去值更小的左子树寻找 LCA。
依据这个思路就可以写出解法代码:
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
# 保证 val1 较小,val2 较大
val1 = min(p.val, q.val)
val2 = max(p.val, q.val)
return self.find(root, val1, val2)
# 在 BST 中寻找 val1 和 val2 的最近公共祖先节点
def find(self, root: 'TreeNode', val1: int, val2: int) -> 'TreeNode':
if root is None:
return None
if root.val > val2:
# 当前节点太大,去左子树找
return self.find(root.left, val1, val2)
if root.val < val1:
# 当前节点太小,去右子树找
return self.find(root.right, val1, val2)
# val1 <= root.val <= val2
# 则当前节点就是最近公共祖先
return root上述代码的可视化面板如下,可以看到在 BST 中寻找最近公共祖先的过程非常快,不需要遍历整棵树:
算法可视化面板
1650. 二叉树的最近公共祖先 III
再看最后一道最近公共祖先的题目吧,力扣第 1650 题「二叉树的最近公共祖先 III」,这次输入的二叉树节点比较特殊,包含指向父节点的指针。题目会给你输入一棵存在于二叉树中的两个节点 p 和 q,请你返回它们的最近公共祖先。函数签名如下:
class Node:
def __init__(self):
self.val = None
self.left = None
self.right = None
self.parent = None
# 函数签名
def lowestCommonAncestor(p: Node, q: Node) -> Node:由于节点中包含父节点的指针,所以二叉树的根节点就没必要输入了。
这道题其实不是公共祖先的问题,而是单链表相交的问题,你把 parent 指针想象成单链表的 next 指针,题目就变成了:
给你输入两个单链表的头结点 p 和 q,这两个单链表必然会相交,请你返回相交点。
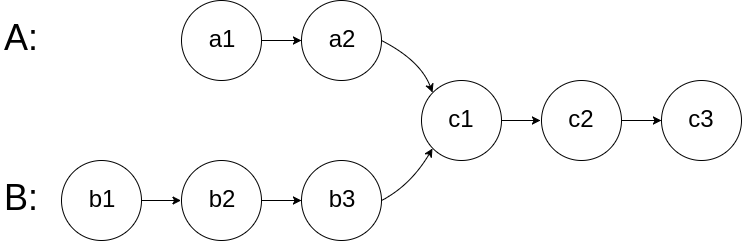
我在前文 单链表的六大解题套路 中详细讲解过求链表交点的问题,具体思路在本文就不展开了,直接给出本题的解法代码:
class Solution:
# 施展链表双指针技巧
def lowestCommonAncestor(self, p: 'Node', q: 'Node') -> 'Node':
a, b = p, q
while a != b:
# a 走一步,如果走到根节点,转到 q 节点
if a is None:
a = q
else:
a = a.parent
# b 走一步,如果走到根节点,转到 p 节点
if b is None:
b = p
else:
b = b.parent
return a上述代码的可视化面板如下,可以多次点击 这一行代码查看两个指针交替移动的过程:
算法可视化面板
至此,5 道最近公共祖先的题目就全部讲完了,前 3 道题目从一个基本的 find 函数衍生出解法,后 2 道比较特殊,分别利用了 BST 和单链表相关的技巧,希望本文对你有启发。
拓展:如何计算完全二叉树的节点数
如果让你数一下一棵普通二叉树有多少个节点,这很简单,只要在二叉树的遍历框架上加一点代码就行了。
但是,力扣第第 222 题「完全二叉树的节点个数」给你一棵完全二叉树,让你计算它的节点个数,你会不会?算法的时间复杂度是多少?
这个算法的时间复杂度应该是$ O(logN∗logN),如果你心中的算法没有达到这么高效,那么本文就是给你写的。
关于「完全二叉树」和「满二叉树」等名词的定义,可以参考基础知识章节的 二叉树基础。
一、思路分析
现在回归正题,如何求一棵完全二叉树的节点个数呢?
# 输入一棵完全二叉树,返回节点总数
def countNodes(root: TreeNode) -> int:如果是一个普通二叉树,显然只要向下面这样遍历一边即可,时间复杂度 $O(N)$:
def countNodes(root: TreeNode) -> int:
if root == None:
return 0
return 1 + countNodes(root.left) + countNodes(root.right)那如果是一棵满二叉树,节点总数就和树的高度呈指数关系:
def countNodes(root: TreeNode) -> int:
h = 0
# 计算树的高度
while root:
root = root.left
h += 1
# 节点总数就是 2^h - 1
return 2 ** h - 1完全二叉树比普通二叉树特殊,但又没有满二叉树那么特殊,计算它的节点总数,可以说是普通二叉树和完全二叉树的结合版,先看代码:
class Solution:
def countNodes(self, root: TreeNode) -> int:
l = root
r = root
hl = 0
hr = 0
# 沿最左侧和最右侧分别计算高度
while l is not None:
l = l.left
hl += 1
while r is not None:
r = r.right
hr += 1
# 如果左右侧计算的高度相同,则是一棵满二叉树
if hl == hr:
return pow(2, hl) - 1
# 如果左右侧的高度不同,则按照普通二叉树的逻辑计算
return 1 + self.countNodes(root.left) + self.countNodes(root.right)算法可视化面板
结合刚才针对满二叉树和普通二叉树的算法,上面这段代码应该不难理解,就是一个结合版,但是其中降低时间复杂度的技巧是非常微妙的。
二、复杂度分析
开头说了,这个算法的时间复杂度是 $O(logN×logN)$,这是怎么算出来的呢?
直觉感觉好像最坏情况下是 $O(N×logN)$ 吧,因为之前的 while 需要$ logN$的时间,最后要 $O(N)$ 的时间向左右子树递归:
return 1 + countNodes(root.left) + countNodes(root.right);关键点在于,这两个递归只有一个会真的递归下去,另一个一定会触发 hl == hr 而立即返回,不会递归下去。
为什么呢?原因如下:
一棵完全二叉树的两棵子树,至少有一棵是满二叉树:
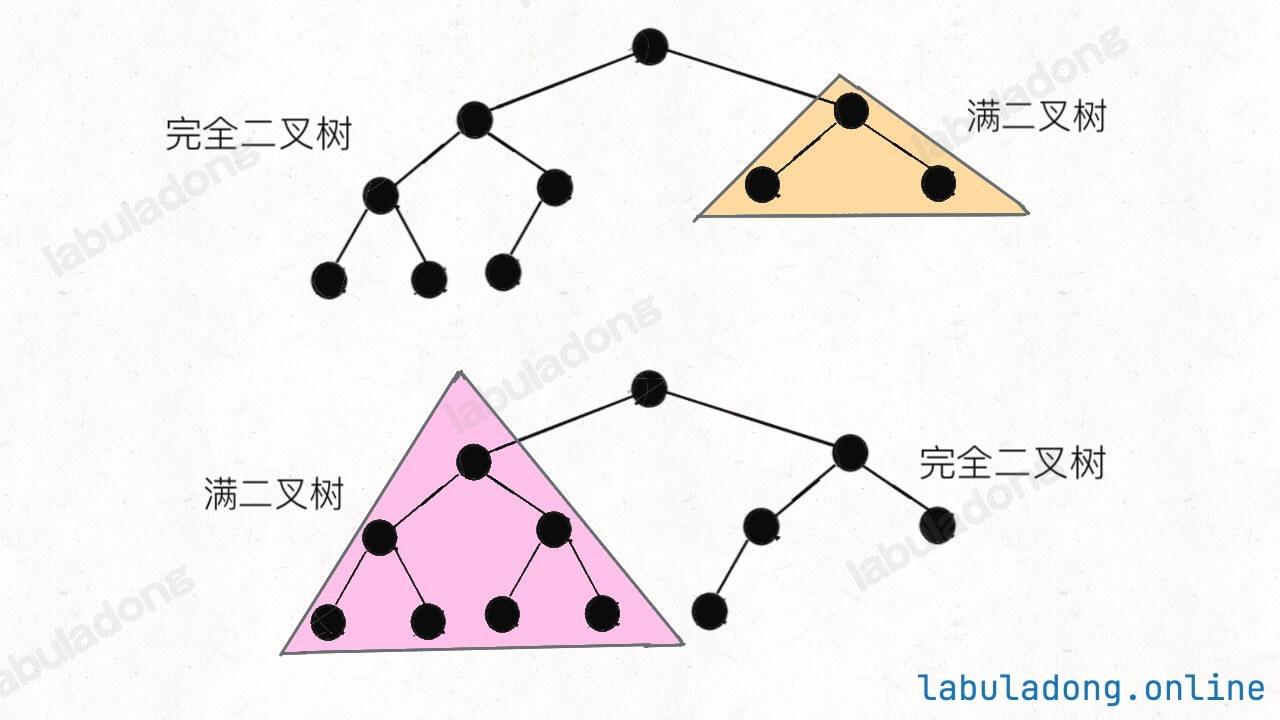
看图就明显了吧,由于完全二叉树的性质,其子树一定有一棵是满的,所以一定会触发 hl == hr,只消耗 $O*(log*N)$ 的复杂度而不会继续递归。
综上,算法的递归深度就是树的高度 $ O(logN) $,每次递归所花费的时间就是 while 循环,需要 $O(logN)$,所以总体的时间复杂度是$O(logN×logN)$。
所以说,「完全二叉树」这个概念还是有它存在的原因的,不仅适用于数组实现二叉堆,而且连计算节点总数这种看起来简单的操作都有高效的算法实现。
拓展:惰性展开多叉树
一、题目描述
这是力扣第 341 题「扁平化嵌套列表迭代器」:
341. 扁平化嵌套列表迭代器 | 力扣
给你一个嵌套的整数列表 nestedList 。每个元素要么是一个整数,要么是一个列表;该列表的元素也可能是整数或者是其他列表。请你实现一个迭代器将其扁平化,使之能够遍历这个列表中的所有整数。
实现扁平迭代器类 NestedIterator :
NestedIterator(List<NestedInteger> nestedList)用嵌套列表nestedList初始化迭代器。int next()返回嵌套列表的下一个整数。boolean hasNext()如果仍然存在待迭代的整数,返回true;否则,返回false。
你的代码将会用下述伪代码检测:
initialize iterator with nestedList
res = []
while iterator.hasNext()
append iterator.next() to the end of res
return res如果 res 与预期的扁平化列表匹配,那么你的代码将会被判为正确。
示例 1:
输入:nestedList = [[1,1],2,[1,1]]
输出:[1,1,2,1,1]
解释:通过重复调用 next 直到 hasNext 返回 false,next 返回的元素的顺序应该是: [1,1,2,1,1]。示例 2:
输入:nestedList = [1,[4,[6]]]
输出:[1,4,6]
解释:通过重复调用 next 直到 hasNext 返回 false,next 返回的元素的顺序应该是: [1,4,6]。
提示:
1 <= nestedList.length <= 500- 嵌套列表中的整数值在范围
[-106, 106]内
我们的算法会被输入一个 NestedInteger 列表,我们需要做的就是写一个迭代器类 NestedIterator,将这个带有嵌套结构 NestedInteger 的列表「拍平」:
class NestedIterator:
def __init__(self, nestedList: List[NestedInteger]):
# 构造器输入一个 NestedInteger 列表
pass
# 返回下一个整数
def next(self) -> int:
pass
# 是否还有下一个元素?
def hasNext(self) -> bool:
pass我们写的这个 NestedIterator 类会被这样调用,先调用 hasNext 方法,后调用 next 方法:
NestedIterator i = new NestedIterator(nestedList);
while (i.hasNext())
print(i.next());学过设计模式的朋友应该知道,迭代器也是设计模式的一种,目的就是为调用者屏蔽底层数据结构的细节,简单地通过 hasNext 和 next 方法有序地进行遍历。
为什么说这个题目很有启发性呢?因为我最近在用一款类似印象笔记的软件,叫做 Notion(挺有名的)。这个软件的一个亮点就是「万物皆 block」,比如说标题、页面、表格都是 block。有的 block 甚至可以无限嵌套,这就打破了传统笔记本「文件夹」->「笔记本」->「笔记」的三层结构。
回想这个算法问题,NestedInteger 结构实际上也是一种支持无限嵌套的结构,而且可以同时表示整数和列表两种不同类型,我想 Notion 的核心数据结构 block 估计也是这样的一种设计思路。
那么话说回来,对于这个算法问题,我们怎么解决呢?NestedInteger 结构可以无限嵌套,怎么把这个结构「打平」,为迭代器的调用者屏蔽底层细节,得到扁平化的输出呢?
二、解题思路
显然,NestedInteger 这个神奇的数据结构是问题的关键,不过题目专门提醒我们不要尝试去实现它,也不要去猜测它的实现。
为什么?凭什么?是不是题目在误导我?是不是我进行推测之后,这道题就不攻自破了?
你不让推测,我就偏偏要去推测!我反手就把 NestedInteger 这个结构给实现出来:
# 定义嵌套整型类
class NestedInteger:
# 嵌套整型类型,通过一个整数初始化
def __init__(self, val: int = None, lst: List['NestedInteger'] = None):
# 当前嵌套整型类的整型值
self.val = val
# 当前嵌套整型类嵌套的整型类列表
self.lst = lst
# 如果其中存的是一个整数,则返回 true,否则返回 false
def isInteger(self) -> bool:
return self.val is not None
# 如果其中存的是一个整数,则返回这个整数,否则返回 null
def getInteger(self) -> int:
return self.val
# 如果其中存的是一个列表,则返回这个列表,否则返回 null
def getList(self) -> List['NestedInteger']:
return self.lst嗯,其实这个实现也不难嘛,写出来之后,我不禁翻出前文 多叉树基础及遍历,发现这玩意儿竟然……
class NestedInteger:
def __init__(self):
self.val = None
self.list = []
# 基本的 N 叉树节点
class TreeNode:
def __init__(self, val):
self.val = val
self.children = []这玩意儿不就是棵 N 叉树吗?叶子节点是 Integer 类型,其 val 字段非空;其他节点都是 List<NestedInteger> 类型,其 val 字段为空,但是 list 字段非空,装着孩子节点。
比如说输入是 [[1,1],2,[1,1]],其实就是如下树状结构:
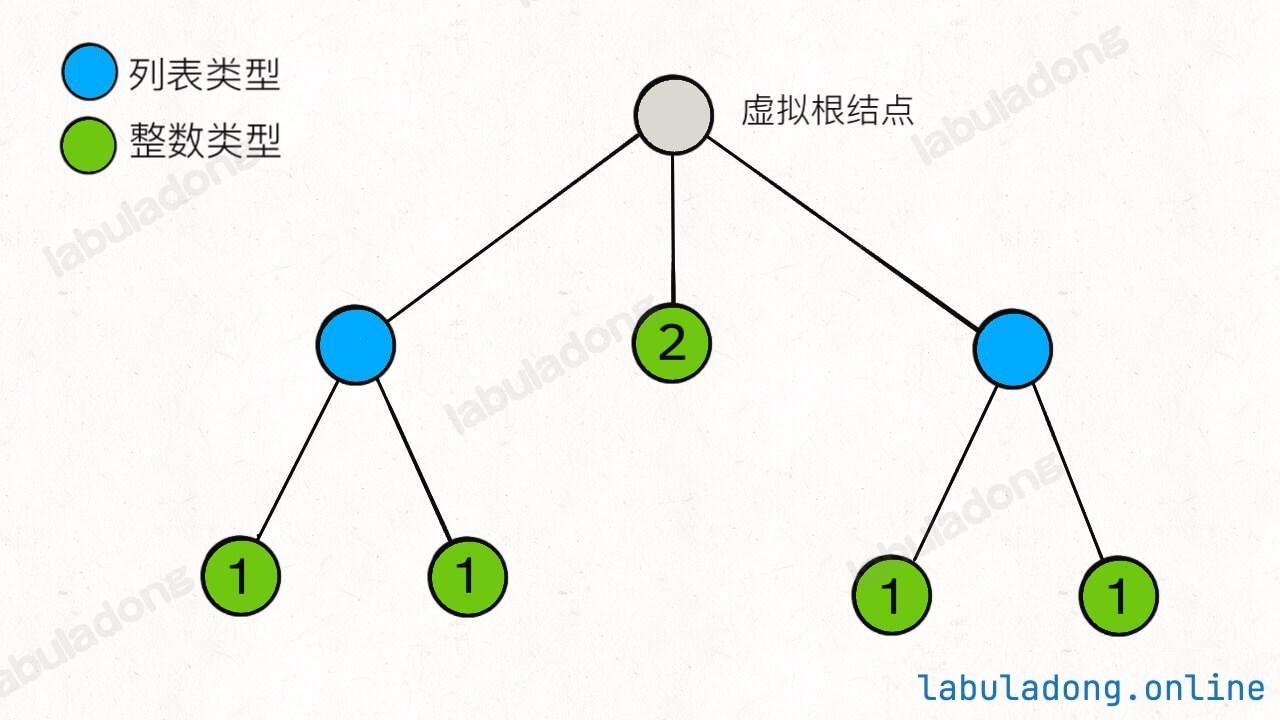
好的,刚才题目说什么来着?把一个 NestedInteger 扁平化对吧?这不就等价于遍历一棵 N 叉树的所有「叶子节点」吗?我把所有叶子节点都拿出来,不就可以作为迭代器进行遍历了吗?
N 叉树的遍历怎么整?我又不禁翻出前文 多叉树遍历框架:
def traverse(root: TreeNode):
if root is None:
return
for child in root.children:
traverse(child)这个框架可以遍历所有节点,而我们只对整数型的 NestedInteger 感兴趣,也就是我们只想要「叶子节点」,所以 traverse 函数只要在到达叶子节点的时候把 val 加入结果列表即可:
class NestedIterator:
def __init__(self, nestedList: List[NestedInteger]):
# 存放将 nestedList 打平的结果
result = []
for node in nestedList:
# 以每个节点为根遍历
self.traverse(node, result)
self.index = 0
self.result = result
def traverse(self, root, result):
if root.isInteger():
# 到达叶子节点
result.append(root.getInteger())
return
# 遍历框架
for child in root.getList():
self.traverse(child, result)
def next(self) -> int:
res = self.result[self.index]
self.index += 1
return res
def hasNext(self) -> bool:
return self.index < len(self.result)这样,我们就把原问题巧妙转化成了一个 N 叉树的遍历问题,并且得到了解法。
三、进阶思路
以上解法虽然可以通过,但是在面试中,也许是有瑕疵的。
我们的解法中,一次性算出了所有叶子节点的值,全部装到 result 列表,也就是内存中,next 和 hasNext 方法只是在对 result 列表做迭代。如果输入的规模非常大,构造函数中的计算就会很慢,而且很占用内存。
一般的迭代器求值应该是「惰性的」,也就是说,如果你要一个结果,我就算一个(或是一小部分)结果出来,而不是一次把所有结果都算出来。
如果想做到这一点,使用递归函数进行 DFS 遍历肯定是不行的,而且我们其实只关心「叶子节点」,所以传统的 BFS 算法也不行。实际的思路很简单:
调用 hasNext 时,如果 nestedList 的第一个元素是列表类型,则不断展开这个元素,直到第一个元素是整数类型。
仔细想一下这个过程应该就能理解了,一次只展开一个最内层的 nestedList,不会一次性把所有 nestedList 展开,相当于惰性的 DFS 遍历。
由于调用 next 方法之前一定会调用 hasNext 方法,这就可以保证每次调用 next 方法的时候第一个元素是整数型,直接返回并删除第一个元素即可。
看一下代码:
class NestedIterator:
def __init__(self, nestedList: [NestedInteger]):
# 不直接用 nestedList 的引用,是因为不能确定它的底层实现
# 必须保证是 LinkedList,否则下面的 addFirst 会很低效
self.list = collections.deque(nestedList)
def next(self) -> int:
# hasNext 方法保证了第一个元素一定是整数类型
return self.list.popleft().getInteger()
def hasNext(self) -> bool:
# 循环拆分列表元素,直到列表第一个元素是整数类型
while self.list and not self.list[0].isInteger():
# 当列表开头第一个元素是列表类型时,进入循环
first = self.list.popleft().getList()
# 将第一个列表打平并按顺序添加到开头
for i in range(len(first) - 1, -1, -1):
self.list.appendleft(first[i])
return bool(self.list)以这种方法,符合迭代器惰性求值的特性,是比较好的解法。
拓展:归并排序详解及应用
一直都有很多读者说,想让我用框架思维讲一讲基本的排序算法,我觉得确实得讲讲,毕竟学习任何东西都讲求一个融会贯通,只有对其本质进行比较深刻的理解,才能运用自如。
本文就先讲归并排序,给一套代码模板,然后讲讲它在算法问题中的应用。阅读本文前我希望你读过前文 手把手刷二叉树(纲领篇)。
我在讲二叉树的时候,提了一嘴归并排序,说归并排序就是二叉树的后序遍历,当时就有很多读者留言说醍醐灌顶。
知道为什么很多读者遇到递归相关的算法就觉得烧脑吗?因为还处在「看山是山,看水是水」的阶段。
就说归并排序吧,如果给你看代码,让你脑补一下归并排序的过程,你脑子里会出现什么场景?
这是一个数组排序算法,所以你脑补一个数组的 GIF,在那一个个交换元素?如果是这样的话,那格局就低了。
但如果你脑海中浮现出的是一棵二叉树,甚至浮现出二叉树后序遍历的场景,那格局就高了,大概率掌握了我经常强调的 框架思维,用这种抽象能力学习算法就省劲多了。
那么,归并排序明明就是一个数组算法,和二叉树有什么关系?接下来我就具体讲讲。
算法思路
就这么说吧,所有递归的算法,你甭管它是干什么的,本质上都是在遍历一棵(递归)树,然后在节点(前中后序位置)上执行代码,你要写递归算法,本质上就是要告诉每个节点需要做什么。
你看归并排序的代码框架:
# 定义:排序 nums[lo..hi]
def sort(nums: List[int], lo: int, hi: int) -> None:
if lo == hi:
return
mid = (lo + hi) // 2
# 利用定义,排序 nums[lo..mid]
sort(nums, lo, mid)
# 利用定义,排序 nums[mid+1..hi]
sort(nums, mid + 1, hi)
# ***** 后序位置 *****
# 此时两部分子数组已经被排好序
# 合并两个有序数组,使 nums[lo..hi] 有序
merge(nums, lo, mid, hi)
# 将有序数组 nums[lo..mid] 和有序数组 nums[mid+1..hi]
# 合并为有序数组 nums[lo..hi]
def merge(nums: List[int], lo: int, mid: int, hi: int) -> None:
pass看这个框架,也就明白那句经典的总结:归并排序就是先把左半边数组排好序,再把右半边数组排好序,然后把两半数组合并。
上述代码和二叉树的后序遍历很像:
# 二叉树遍历框架
def traverse(root: TreeNode) -> None:
if root is None:
return
traverse(root.left)
traverse(root.right)
# 后序位置
print(root.val)再进一步,你联想一下求二叉树的最大深度的算法代码:
# 定义:输入根节点,返回这棵二叉树的最大深度
def maxDepth(root: TreeNode) -> int:
if not root:
return 0
# 利用定义,计算左右子树的最大深度
leftMax = maxDepth(root.left)
rightMax = maxDepth(root.right)
# 整棵树的最大深度等于左右子树的最大深度取最大值,
# 然后再加上根节点自己
res = max(leftMax, rightMax) + 1
return res是不是更像了?
前文 手把手刷二叉树(纲领篇) 说二叉树问题可以分为两类思路,一类是遍历一遍二叉树的思路,另一类是分解问题的思路,根据上述类比,显然归并排序利用的是分解问题的思路(分治算法)。
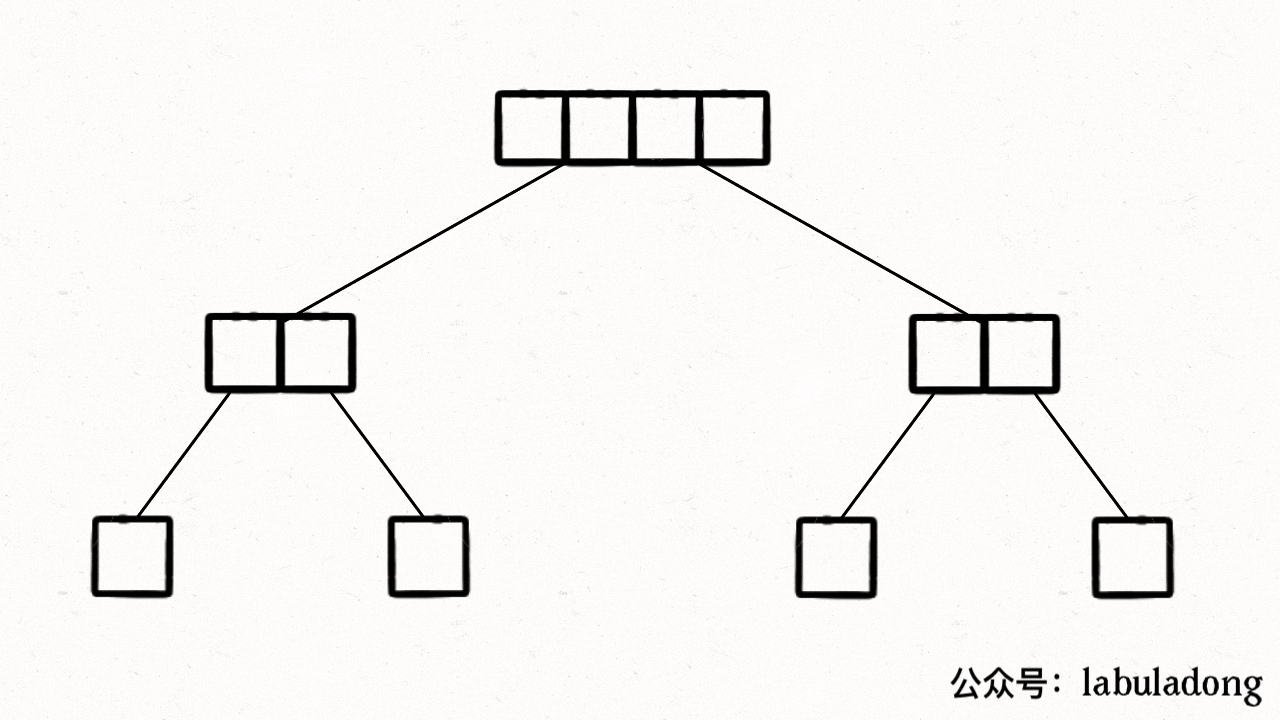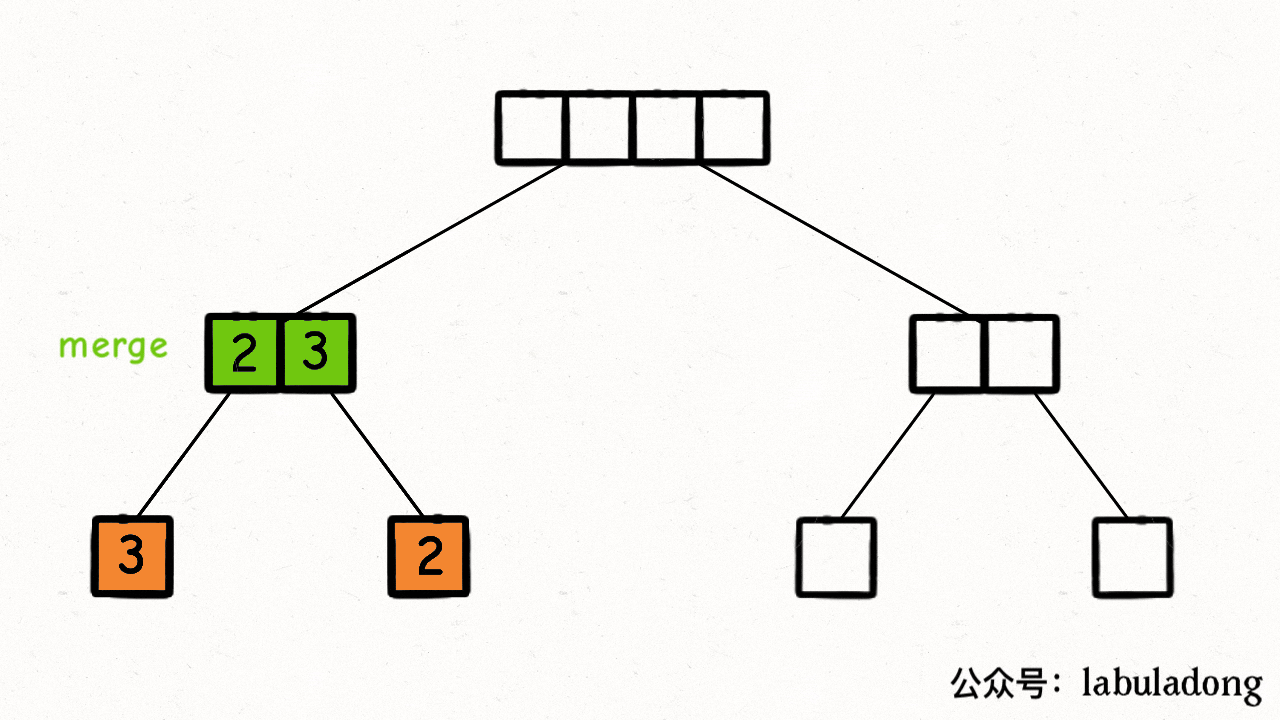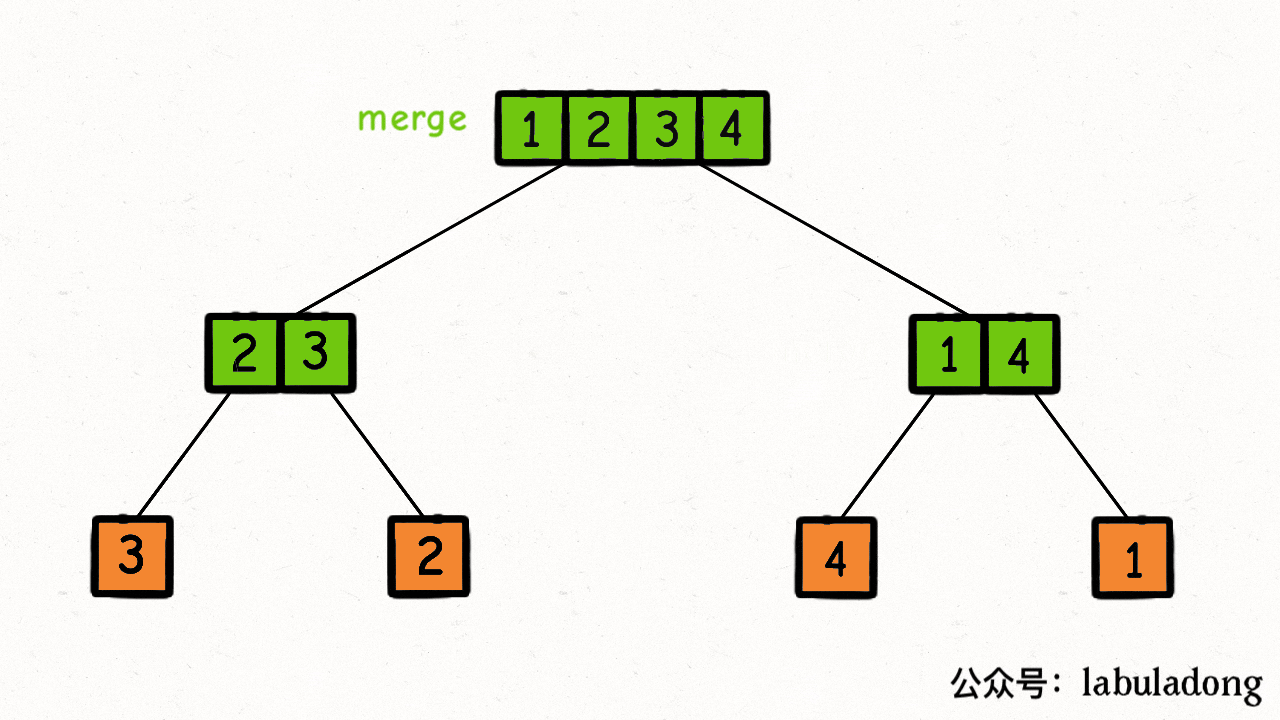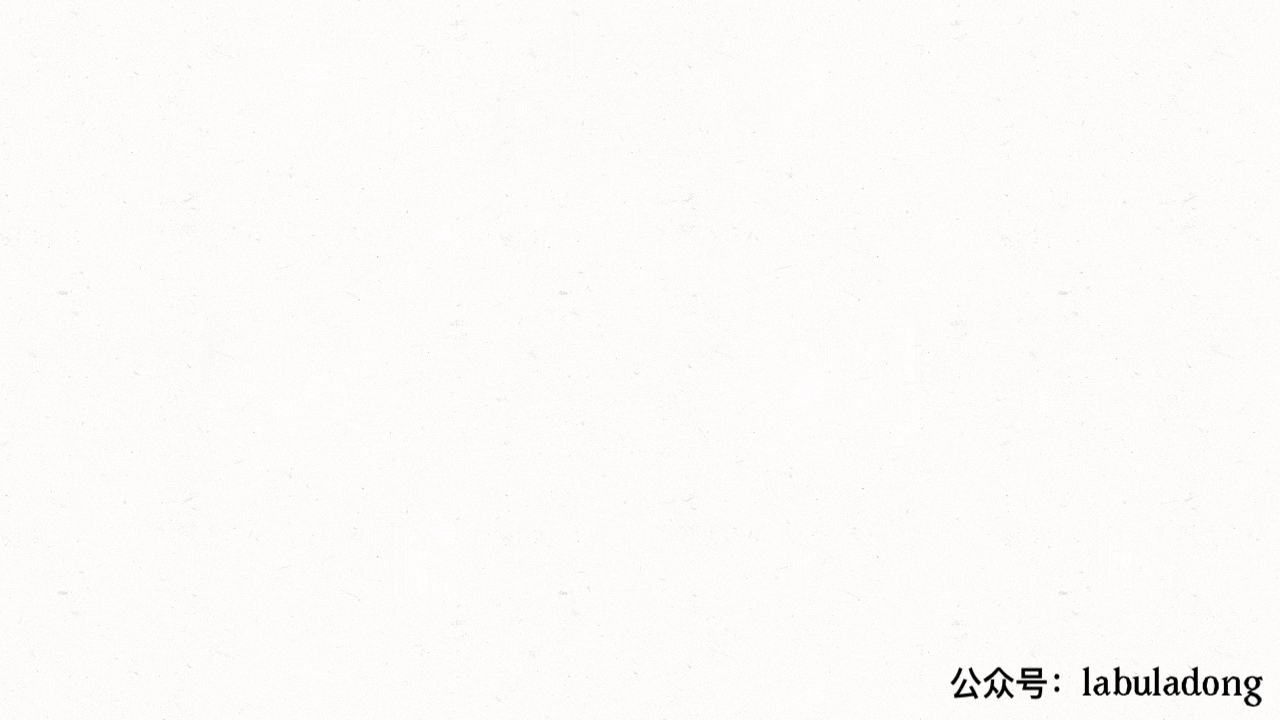
归并排序的过程可以在逻辑上抽象成一棵二叉树,树上的每个节点的值可以认为是 nums[lo..hi],叶子节点的值就是数组中的单个元素:
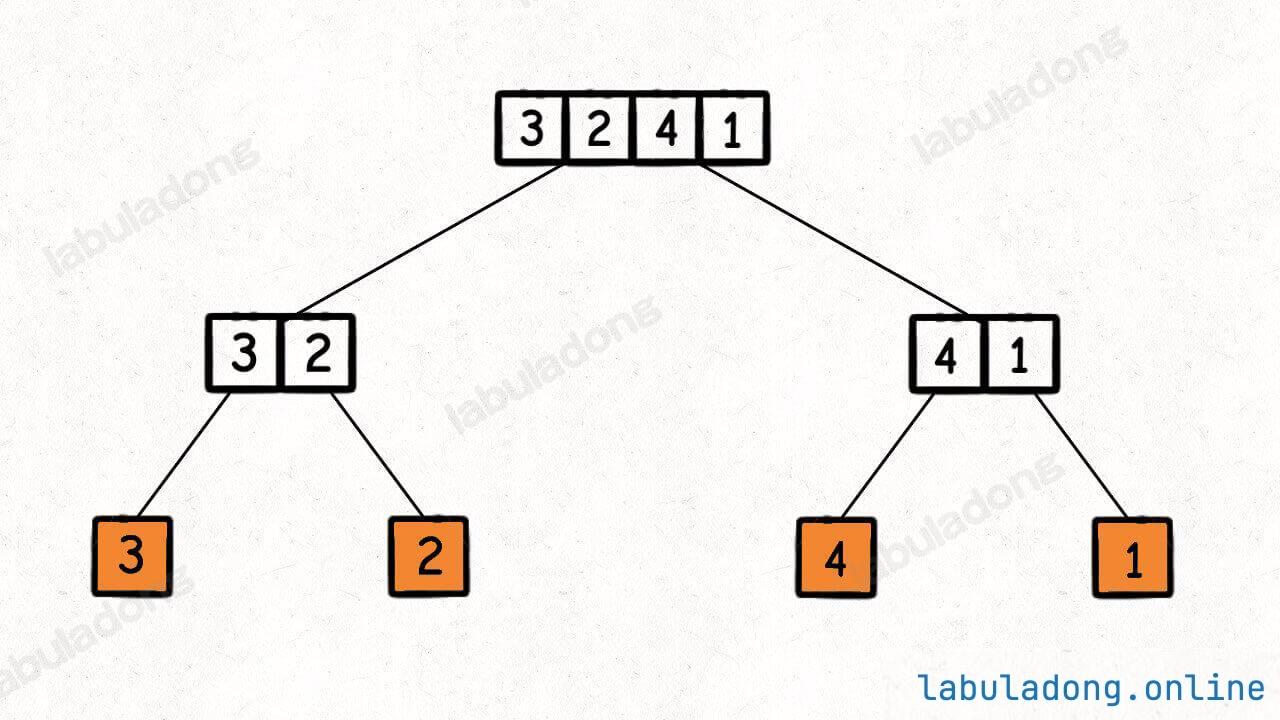
然后,在每个节点的后序位置(左右子节点已经被排好序)的时候执行 merge 函数,合并两个子节点上的子数组:
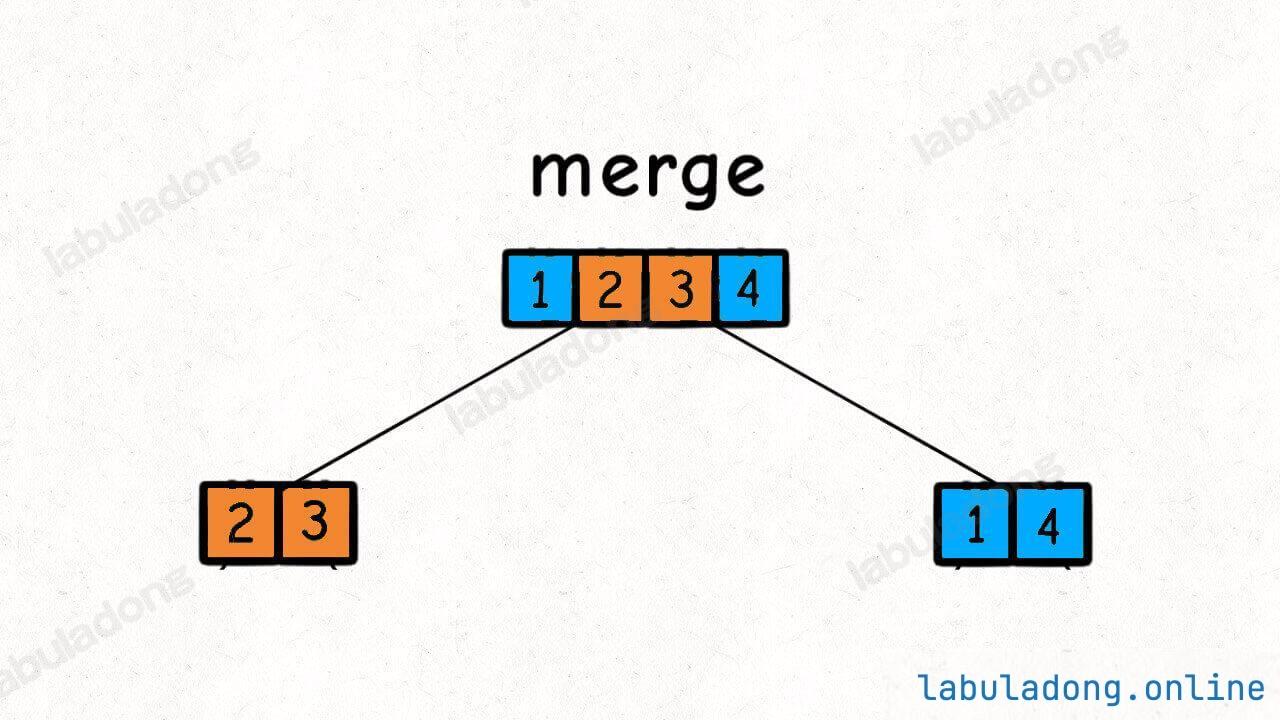
这个 merge 操作会在二叉树的每个节点上都执行一遍,执行顺序是二叉树后序遍历的顺序。
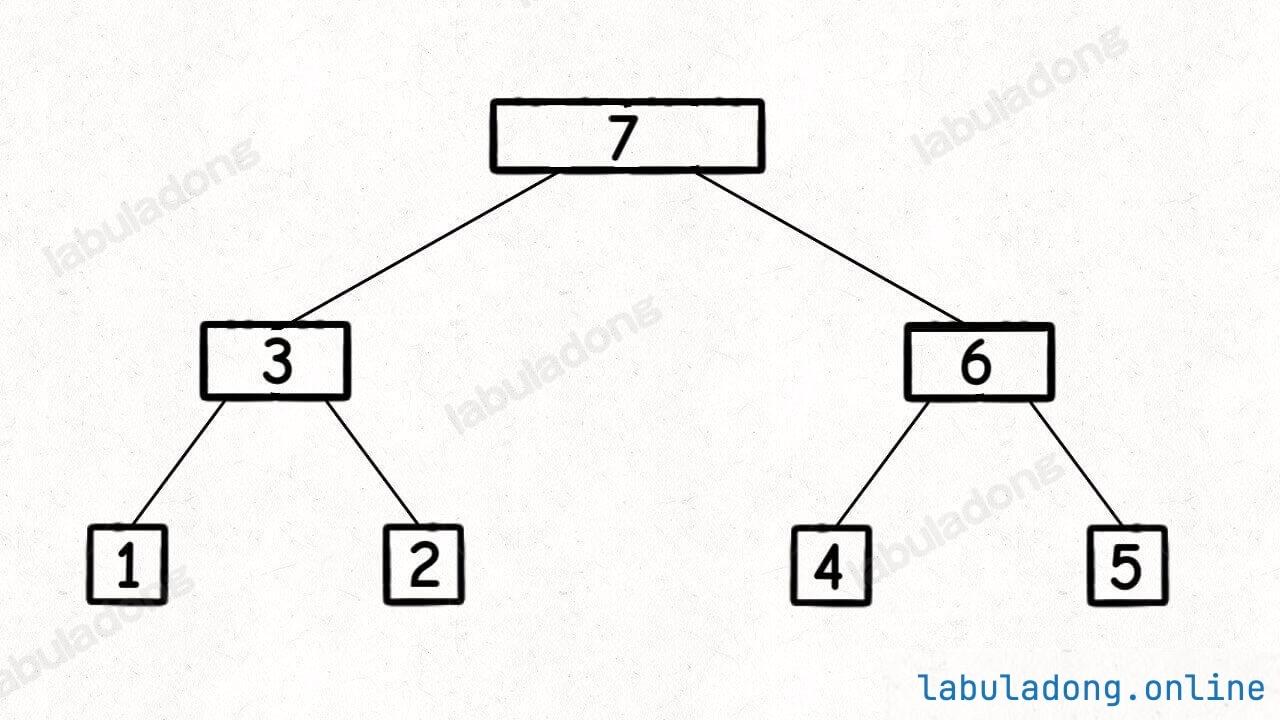
后序遍历二叉树大家应该已经烂熟于心了,就是下图这个遍历顺序:
结合上述基本分析,我们把 nums[lo..hi] 理解成二叉树的节点,sort 函数理解成二叉树的遍历函数,整个归并排序的执行过程就是以下 GIF 描述的这样:
这样,归并排序的核心思路就分析完了,接下来只要把思路翻译成代码就行。
代码实现
只要拥有了正确的思维方式,理解算法思路是不困难的,但把思路实现成代码,也很考验一个人的编程能力。
毕竟算法的时间复杂度只是一个理论上的衡量标准,而算法的实际运行效率要考虑的因素更多,比如应该避免内存的频繁分配释放,代码逻辑应尽可能简洁等等。
这里我参考《算法 4》这本书中归并排序代码给出归并排序的代码实现:
class Merge:
# 用于辅助合并有序数组
temp = []
@staticmethod
def sort(nums):
# 先给辅助数组开辟内存空间
Merge.temp = [0] * len(nums)
# 排序整个数组(原地修改)
Merge._sort(nums, 0, len(nums) - 1)
# 定义:将子数组 nums[lo..hi] 进行排序
@staticmethod
def _sort(nums, lo, hi):
if lo == hi:
# 单个元素不用排序
return
# 这样写是为了防止溢出,效果等同于 (hi + lo) / 2
mid = lo + (hi - lo) // 2
# 先对左半部分数组 nums[lo..mid] 排序
Merge._sort(nums, lo, mid)
# 再对右半部分数组 nums[mid+1..hi] 排序
Merge._sort(nums, mid + 1, hi)
# 将两部分有序数组合并成一个有序数组
Merge.merge(nums, lo, mid, hi)
# 将 nums[lo..mid] 和 nums[mid+1..hi] 这两个有序数组合并成一个有序数组
@staticmethod
def merge(nums, lo, mid, hi):
# 先把 nums[lo..hi] 复制到辅助数组中
# 以便合并后的结果能够直接存入 nums
for i in range(lo, hi+1):
Merge.temp[i] = nums[i]
# 数组双指针技巧,合并两个有序数组
i, j = lo, mid + 1
for p in range(lo, hi+1):
if i == mid + 1:
# 左半边数组已全部被合并
nums[p] = Merge.temp[j]
j += 1
elif j == hi + 1:
# 右半边数组已全部被合并
nums[p] = Merge.temp[i]
i += 1
elif Merge.temp[i] > Merge.temp[j]:
nums[p] = Merge.temp[j]
j += 1
else:
nums[p] = Merge.temp[i]
i += 1有了之前的铺垫,这里只需要着重讲一下这个 merge 函数。
sort 函数对 nums[lo..mid] 和 nums[mid+1..hi] 递归排序完成之后,我们没有办法原地把它俩合并,所以需要 copy 到 temp 数组里面,然后通过类似于前文 单链表的六大技巧 中合并有序链表的双指针技巧将 nums[lo..hi] 合并成一个有序数组:
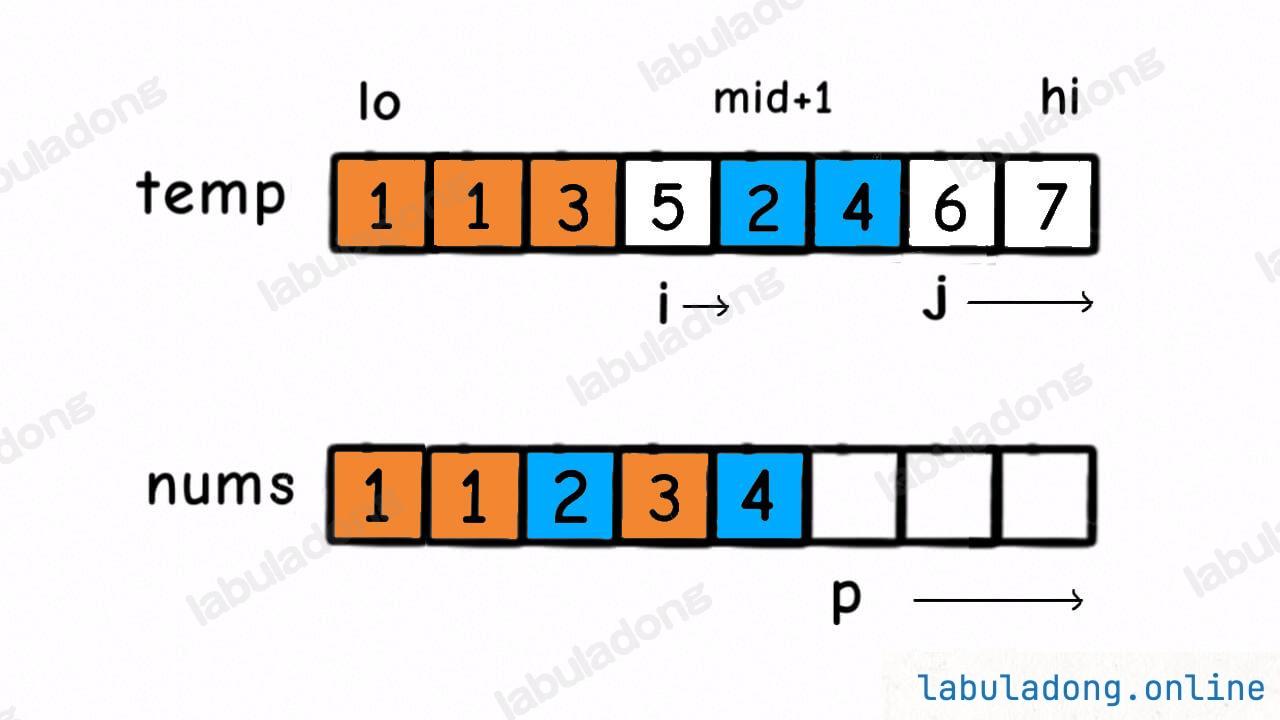
注意我们不是在 merge 函数执行的时候 new 辅助数组,而是提前把 temp 辅助数组 new 出来了,这样就避免了在递归中频繁分配和释放内存可能产生的性能问题。
贴一个归并排序过程的可视化动画,方便大家理解算法运行的过程:
算法可视化面板
复杂度分析
再说一下归并排序的时间复杂度,虽然大伙儿应该都知道是 O(NlogN),但不见得所有人都知道这个复杂度怎么算出来的。
前文 动态规划详解 说过递归算法的复杂度计算,就是子问题个数 x 解决一个子问题的复杂度。对于归并排序来说,时间复杂度显然集中在 merge 函数遍历 nums[lo..hi] 的过程,但每次 merge 输入的 lo 和 hi 都不同,所以不容易直观地看出时间复杂度。
merge 函数到底执行了多少次?每次执行的时间复杂度是多少?总的时间复杂度是多少?这就要结合之前画的这幅图来看:

执行的次数是二叉树节点的个数,每次执行的复杂度就是每个节点代表的子数组的长度,所以总的时间复杂度就是整棵树中「数组元素」的个数。
所以从整体上看,这个二叉树的高度是 logN,其中每一层的元素个数就是原数组的长度 N,所以总的时间复杂度就是 O(NlogN)。
912. 排序数组
力扣第 912 题「排序数组」就是让你对数组进行排序,我们可以直接套用归并排序代码模板:
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
Merge.sort(nums)
return nums
class Merge:
# 见上文315. 计算右侧小于当前元素的个数
除了最基本的排序问题,归并排序还可以用来解决力扣第 315 题「计算右侧小于当前元素的个数」:
315. 计算右侧小于当前元素的个数 | 力扣 | LeetCode | 🔴
给你一个整数数组 nums ,按要求返回一个新数组 counts 。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例 1:
输入:nums = [5,2,6,1]
输出:[2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1)
2 的右侧仅有 1 个更小的元素 (1)
6 的右侧有 1 个更小的元素 (1)
1 的右侧有 0 个更小的元素
示例 2:
输入:nums = [-1] 输出:[0]
示例 3:
输入:nums = [-1,-1] 输出:[0,0]
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
我用比较数学的语言来描述一下(方便和后续类似题目进行对比),题目让你求出一个 count 数组,使得:
count[i] = COUNT(j) where j > i and nums[j] < nums[i]拍脑袋的暴力解法就不说了,嵌套 for 循环,平方级别的复杂度。
这题和归并排序什么关系呢,主要在 merge 函数,我们在使用 merge 函数合并两个有序数组的时候,其实是可以知道一个元素 nums[i] 后边有多少个元素比 nums[i] 小的。
具体来说,比如这个场景:
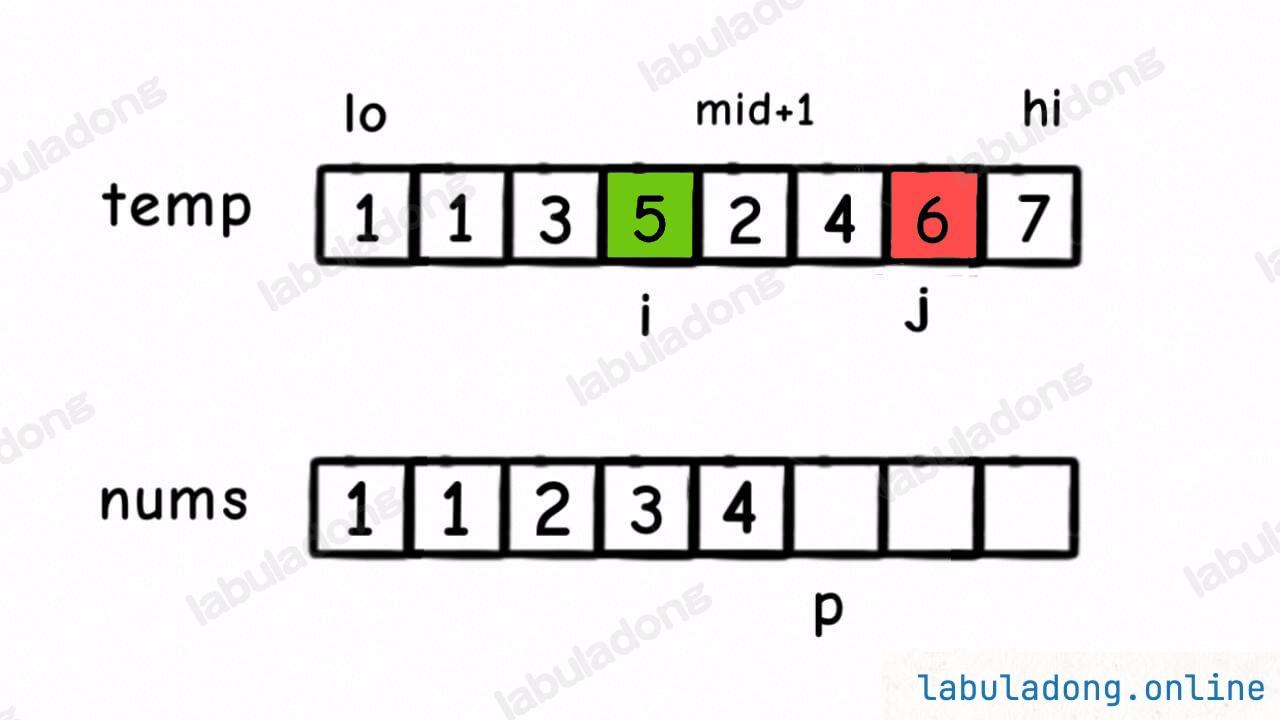
这时候我们应该把 temp[i] 放到 nums[p] 上,因为 temp[i] < temp[j]。
但就在这个场景下,我们还可以知道一个信息:5 后面比 5 小的元素个数就是 左闭右开区间 [mid + 1, j) 中的元素个数,即 2 和 4 这两个元素:
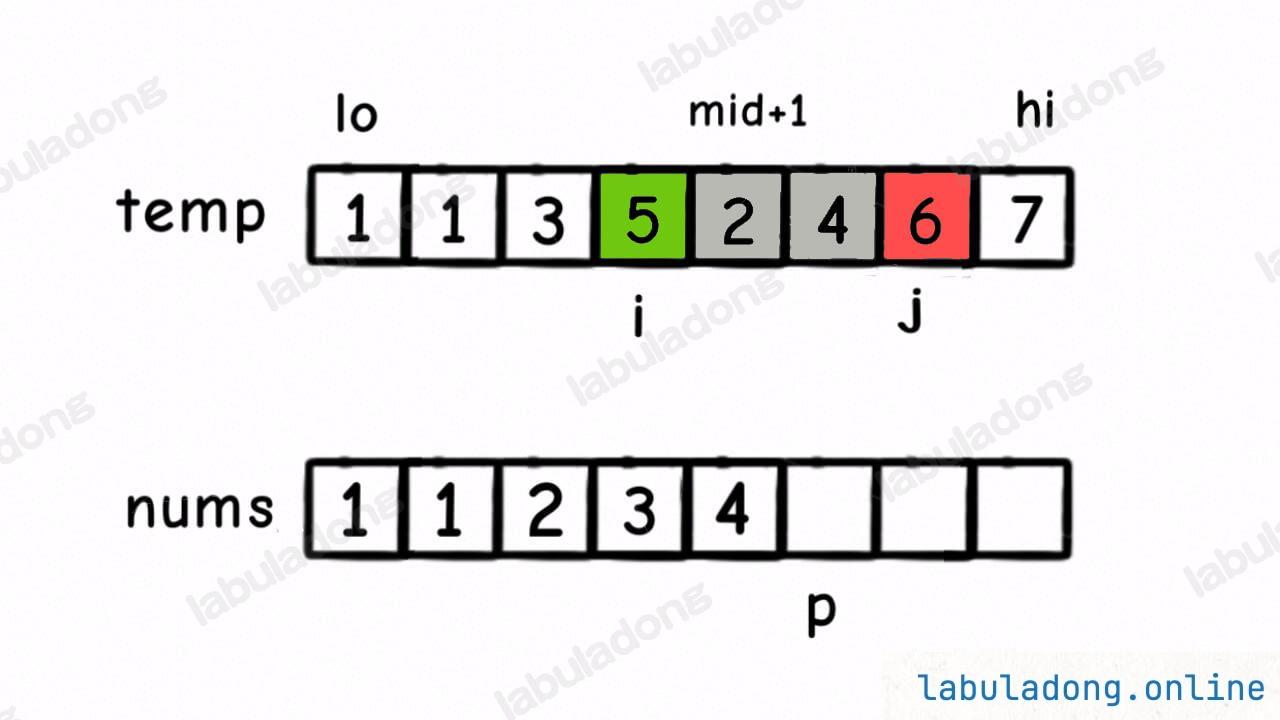
换句话说,在对 nums[lo..hi] 合并的过程中,每当执行 nums[p] = temp[i] 时,就可以确定 temp[i] 这个元素后面比它小的元素个数为 j - mid - 1。
当然,nums[lo..hi] 本身也只是一个子数组,这个子数组之后还会被执行 merge,其中元素的位置还是会改变。但这是其他递归节点需要考虑的问题,我们只要在 merge 函数中做一些手脚,叠加每次 merge 时记录的结果即可。
发现了这个规律后,我们只要在 merge 中添加两行代码即可解决这个问题,看解法代码:
class Solution:
class Pair:
def __init__(self, val, id):
# 记录数组的元素值
self.val = val
# 记录元素在数组中的原始索引
self.id = id
# 归并排序所用的辅助数组
temp = []
# 记录每个元素后面比自己小的元素个数
count = []
# 主函数
def countSmaller(self, nums):
n = len(nums)
self.count = [0] * n
self.temp = [self.Pair(0, 0)] * n
arr = []
# 记录元素原始的索引位置,以便在 count 数组中更新结果
for i in range(n):
arr.append(self.Pair(nums[i], i))
# 执行归并排序,本题结果被记录在 count 数组中
self.sort(arr, 0, n - 1)
res = []
for c in self.count:
res.append(c)
return res
# 归并排序
def sort(self, arr, lo, hi):
if lo == hi:
return
mid = lo + (hi - lo) // 2
self.sort(arr, lo, mid)
self.sort(arr, mid + 1, hi)
self.merge(arr, lo, mid, hi)
# 合并两个有序数组
def merge(self, arr, lo, mid, hi):
for i in range(lo, hi + 1):
self.temp[i] = arr[i]
i, j = lo, mid + 1
for p in range(lo, hi + 1):
if i == mid + 1:
arr[p] = self.temp[j]
j += 1
elif j == hi + 1:
arr[p] = self.temp[i]
i += 1
# 更新 count 数组
self.count[arr[p].id] += j - mid - 1
elif self.temp[i].val > self.temp[j].val:
arr[p] = self.temp[j]
j += 1
else:
arr[p] = self.temp[i]
i += 1
# 更新 count 数组
self.count[arr[p].id] += j - mid - 1因为在排序过程中,每个元素的索引位置会不断改变,所以我们用一个 Pair 类封装每个元素及其在原始数组 nums 中的索引,以便 count 数组记录每个元素之后小于它的元素个数。
接下来我们再看几道原理类似的题目,都是通过给归并排序的 merge 函数加一些私货完成目标。
493. 翻转对
看一下力扣第 493 题「翻转对」:
493. 翻转对 | 力扣 | LeetCode | 🔴
给定一个数组 nums ,如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。
你需要返回给定数组中的重要翻转对的数量。
示例 1:
输入: [1,3,2,3,1] 输出: 2
示例 2:
输入: [2,4,3,5,1] 输出: 3
注意:
- 给定数组的长度不会超过
50000。 - 输入数组中的所有数字都在32位整数的表示范围内。
我把这道题换个表述方式,你注意和上一道题目对比:
请你先求出一个 count 数组,其中:
count[i] = COUNT(j) where j > i and nums[i] > 2*nums[j]然后请你求出这个 count 数组中所有元素的和。
你看,这样说其实和题目是一个意思,而且和上一道题非常类似,只不过上一题求的是 nums[i] > nums[j],这里求的是 nums[i] > 2*nums[j] 罢了。
所以解题的思路当然还是要在 merge 函数中做点手脚,当 nums[lo..mid] 和 nums[mid+1..hi] 两个子数组完成排序后,对于 nums[lo..mid] 中的每个元素 nums[i],去 nums[mid+1..hi] 中寻找符合条件的 nums[j] 就行了。
看一下我们对上一题 merge 函数的改造:
# 记录「翻转对」的个数
count = 0
# 将 nums[lo..mid] 和 nums[mid+1..hi] 这两个有序数组合并成一个有序数组
def merge(nums, lo, mid, hi):
global count
temp = nums.copy()
# 在合并有序数组之前,加点私货
for i in range(lo, mid + 1):
# 对于左半边的每个 nums[i],都去右半边寻找符合条件的元素
for j in range(mid + 1, hi + 1):
# nums 中的元素可能较大,乘 2 可能溢出,所以转化成 long
if int(nums[i]) > 2 * int(nums[j]):
count += 1
# 数组双指针技巧,合并两个有序数组
i, j = lo, mid + 1
for p in range(lo, hi + 1):
if (i == mid + 1):
nums[p] = temp[j]
j += 1
elif (j == hi + 1):
nums[p] = temp[i]
i += 1
elif temp[i] > temp[j]:
nums[p] = temp[j]
j += 1
else:
nums[p] = temp[i]
i += 1不过呢,这样修改代码会超时,毕竟额外添加了一个嵌套 for 循环。怎么进行优化呢,注意子数组 nums[lo..mid] 是排好序的,也就是 nums[i] <= nums[i+1]。
所以,对于 nums[i], lo <= i <= mid,我们在找到的符合 nums[i] > 2*nums[j] 的 nums[j], mid+1 <= j <= hi,也必然也符合 nums[i+1] > 2*nums[j]。
换句话说,我们不用每次都傻乎乎地去遍历整个 nums[mid+1..hi],只要维护一个开区间边界 end,维护 nums[mid+1..end-1] 是符合条件的元素即可。
看最终的解法代码:
class Solution:
def __init__(self):
# 记录「翻转对」的个数
self.count = 0
self.temp = []
def reversePairs(self, nums) -> int:
# 执行归并排序
self.temp = [0]*len(nums)
self.sort(nums, 0, len(nums) - 1)
return self.count
def sort(self, nums, lo, hi):
# 归并排序
if lo >= hi:
return
mid = lo + (hi - lo) // 2
self.sort(nums, lo, mid)
self.sort(nums, mid + 1, hi)
self.merge(nums, lo, mid, hi)
def merge(self, nums, lo, mid, hi):
for i in range(lo, hi+1):
self.temp[i] = nums[i]
# 维护左闭右开区间 [mid+1, end) 中的元素乘 2 小于 nums[i]
# 为什么 end 是开区间?因为这样的话可以保证初始区间 [mid+1, mid+1) 是一个空区间
end = mid + 1
for i in range(lo, mid+1):
# nums 中的元素可能较大,乘 2 可能溢出,所以转化成 long
while end <= hi and nums[i] > nums[end] * 2:
end += 1
self.count += end - (mid + 1)
# 数组双指针技巧,合并两个有序数组
i, j = lo, mid + 1
for p in range(lo, hi+1):
if i == mid + 1:
nums[p] = self.temp[j]
j += 1
elif j == hi + 1:
nums[p] = self.temp[i]
i += 1
elif self.temp[i] > self.temp[j]:
nums[p] = self.temp[j]
j += 1
else:
nums[p] = self.temp[i]
i += 1327. 区间和的个数
如果你能够理解这道题目,我们最后来看一道难度更大的题目,力扣第 327 题「区间和的个数」:
327. 区间和的个数 | 力扣 | LeetCode | 🔴
给你一个整数数组 nums 以及两个整数 lower 和 upper 。求数组中,值位于范围 [lower, upper] (包含 lower 和 upper)之内的 区间和的个数 。
区间和 S(i, j) 表示在 nums 中,位置从 i 到 j 的元素之和,包含 i 和 j (i ≤ j)。
输入:nums = [-2,5,-1], lower = -2, upper = 2 输出:3 解释:存在三个区间:[0,0]、[2,2] 和 [0,2] ,对应的区间和分别是:-2 、-1 、2 。
示例 2:
输入:nums = [0], lower = 0, upper = 0 输出:1
提示:
1 <= nums.length <= 105-231 <= nums[i] <= 231 - 1-105 <= lower <= upper <= 105- 题目数据保证答案是一个 32 位 的整数
简单说,题目让你计算元素和落在 [lower, upper] 中的所有子数组的个数。
拍脑袋的暴力解法我就不说了,依然是嵌套 for 循环,这里还是说利用归并排序实现的高效算法。
首先,解决这道题需要快速计算子数组的和,所以你需要阅读前文 前缀和数组技巧,创建一个前缀和数组 preSum 来辅助我们迅速计算区间和。
我继续用比较数学的语言来表述下这道题,题目让你通过 preSum 数组求一个 count 数组,使得:
count[i] = COUNT(j) where lower <= preSum[j] - preSum[i] <= upper然后请你求出这个 count 数组中所有元素的和。
你看,这是不是和题目描述一样?preSum 中的两个元素之差其实就是区间和。
有了之前两道题的铺垫,我直接给出这道题的解法代码吧,思路见注释:
class Solution:
def __init__(self):
# 定义实例变量
self.lower = 0
self.upper = 0
self.count = 0
self.temp = []
def countRangeSum(self, nums, lower, upper):
# 赋值实例变量
self.lower = lower
self.upper = upper
# 构建前缀和数组,注意 int 可能溢出,用 long 存储
preSum = [0] * (len(nums) + 1)
for i in range(len(nums)):
preSum[i + 1] = nums[i] + preSum[i]
# 对前缀和数组进行归并排序
self.temp = [0] * len(preSum)
self.sort(preSum, 0, len(preSum) - 1)
return self.count
def sort(self, nums, lo, hi):
if lo == hi:
return
mid = lo + (hi - lo) // 2
self.sort(nums, lo, mid)
self.sort(nums, mid + 1, hi)
self.merge(nums, lo, mid, hi)
def merge(self, nums, lo, mid, hi):
# 填充 temp 数组
for i in range(lo, hi + 1):
self.temp[i] = nums[i]
# 在合并有序数组之前加点私货(这段代码会超时)
# for i in range(lo, mid + 1):
# for j in range(mid + 1, hi + 1):
# 寻找符合条件的 nums[j]
#
# delta = nums[j] - nums[i]
# if delta <= self.upper and delta >= self.lower:
# self.count += 1
# 进行效率优化
# 维护左闭右开区间 [start, end) 中的元素和 nums[i] 的差在 [lower, upper] 中
start = mid + 1
end = mid + 1
for i in range(lo, mid + 1):
# 如果 nums[i] 对应的区间是 [start, end),
# 那么 nums[i+1] 对应的区间一定会整体右移,类似滑动窗口
while start <= hi and nums[start] - nums[i] < self.lower:
start += 1
while end <= hi and nums[end] - nums[i] <= self.upper:
end += 1
self.count += end - start
# 数组双指针技巧,合并两个有序数组
i, j = lo, mid + 1
for p in range(lo, hi + 1):
if i == mid + 1:
nums[p] = self.temp[j]
j += 1
elif j == hi + 1:
nums[p] = self.temp[i]
i += 1
elif self.temp[i] > self.temp[j]:
nums[p] = self.temp[j]
j += 1
else:
nums[p] = self.temp[i]
i += 1我们依然在 merge 函数合并有序数组之前加了一些逻辑,如果看过前文 滑动窗口核心框架,这个效率优化有点类似维护一个滑动窗口,让窗口中的元素和 nums[i] 的差落在 [lower, upper] 中。
归并排序相关的题目到这里就讲完了,你现在回头体会下我在本文开头说那句话:
所有递归的算法,本质上都是在遍历一棵(递归)树,然后在节点(前中后序位置)上执行代码。你要写递归算法,本质上就是要告诉每个节点需要做什么。
比如本文讲的归并排序算法,递归的 sort 函数就是二叉树的遍历函数,而 merge 函数就是在每个节点上做的事情,有没有品出点味道?
最后总结一下吧,本文从二叉树的角度讲了归并排序的核心思路和代码实现,同时讲了几道归并排序相关的算法题。这些算法题其实就是归并排序算法逻辑中夹杂一点私货,但仍然属于比较难的,你可能需要亲自做一遍才能理解。
那我最后留一个思考题吧,下一篇文章我会讲快速排序,你是否能够尝试着从二叉树的角度去理解快速排序?如果让你用一句话总结快速排序的逻辑,你怎么描述?
好了,答案在下篇文章 快速排序详解及应用 揭晓。
拓展:快速排序详解及应用
前文 归并排序算法详解 通过二叉树的视角描述了归并排序的算法原理以及应用,很多读者大呼精妙,那我就趁热打铁,今天继续用二叉树的视角讲一讲快速排序算法的原理以及运用。
快速排序算法思路
首先我们看一下快速排序的代码框架:
def sort(nums: List[int], lo: int, hi: int):
if lo >= hi:
return
# ****** 前序位置 ******
# 对 nums[lo..hi] 进行切分,将 nums[p] 排好序
# 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
p = partition(nums, lo, hi)
# 去左右子数组进行切分
sort(nums, lo, p - 1)
sort(nums, p + 1, hi)其实你对比之后可以发现,快速排序就是一个二叉树的前序遍历:
# 二叉树遍历框架
def traverse(root: TreeNode):
if not root:
return
# 前序位置
print(root.val)
traverse(root.left)
traverse(root.right)另外,前文 归并排序详解 用一句话总结了归并排序:先把左半边数组排好序,再把右半边数组排好序,然后把两半数组合并。
同时我提了一个问题,让你一句话总结快速排序,这里说一下我的答案:
快速排序是先将一个元素排好序,然后再将剩下的元素排好序。
为什么这么说呢,且听我慢慢道来。
快速排序的核心无疑是 partition 函数,partition 函数的作用是在 nums[lo..hi] 中寻找一个切分点 p,通过交换元素使得 nums[lo..p-1] 都小于等于 nums[p],且 nums[p+1..hi] 都大于 nums[p]:
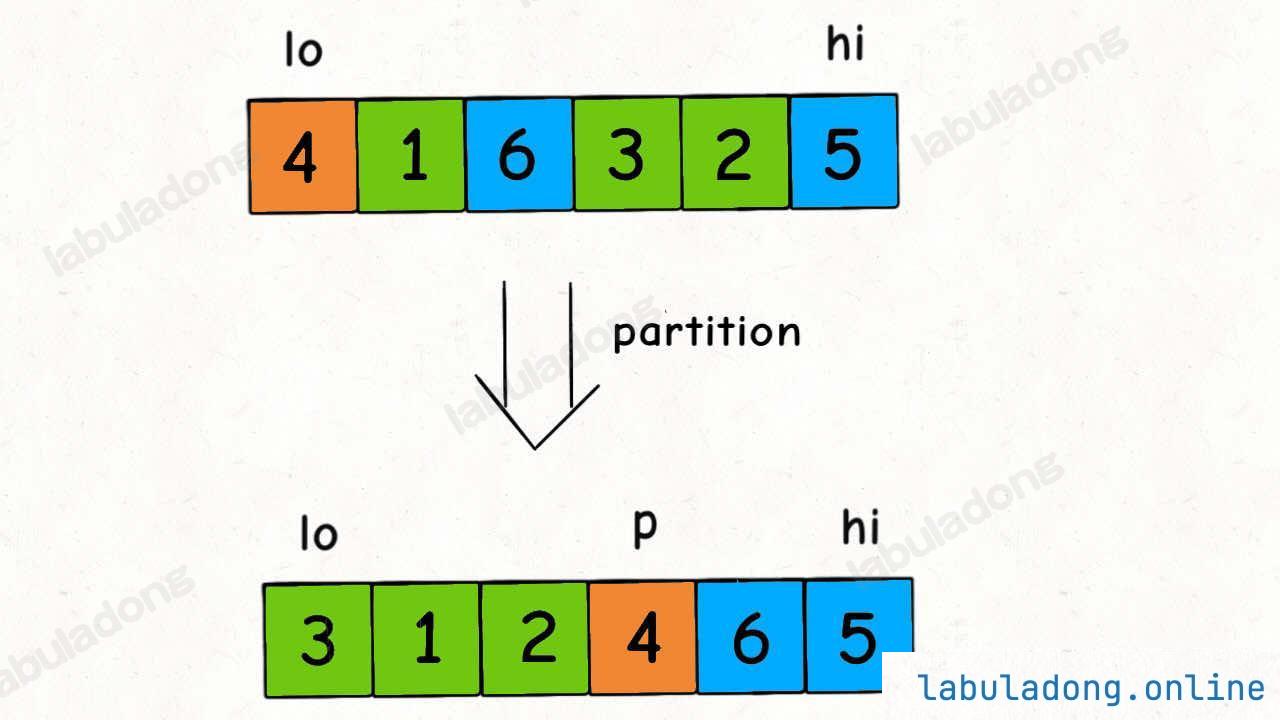
一个元素左边的元素都比它小,右边的元素都比它大,啥意思?不就是它自己已经被放到正确的位置上了吗?
所以 partition 函数干的事情,其实就是把 nums[p] 这个元素排好序了。
一个元素被排好序了,然后呢?你再把剩下的元素排好序不就得了。
剩下的元素有哪些?左边一坨,右边一坨,去吧,对子数组进行递归,用 partition 函数把剩下的元素也排好序。
从二叉树的视角,我们可以把子数组 nums[lo..hi] 理解成二叉树节点上的值,sort 函数理解成二叉树的遍历函数。
参照二叉树的前序遍历顺序,快速排序的运行过程如下 GIF:

你注意最后形成的这棵二叉树是什么?是一棵二叉搜索树:
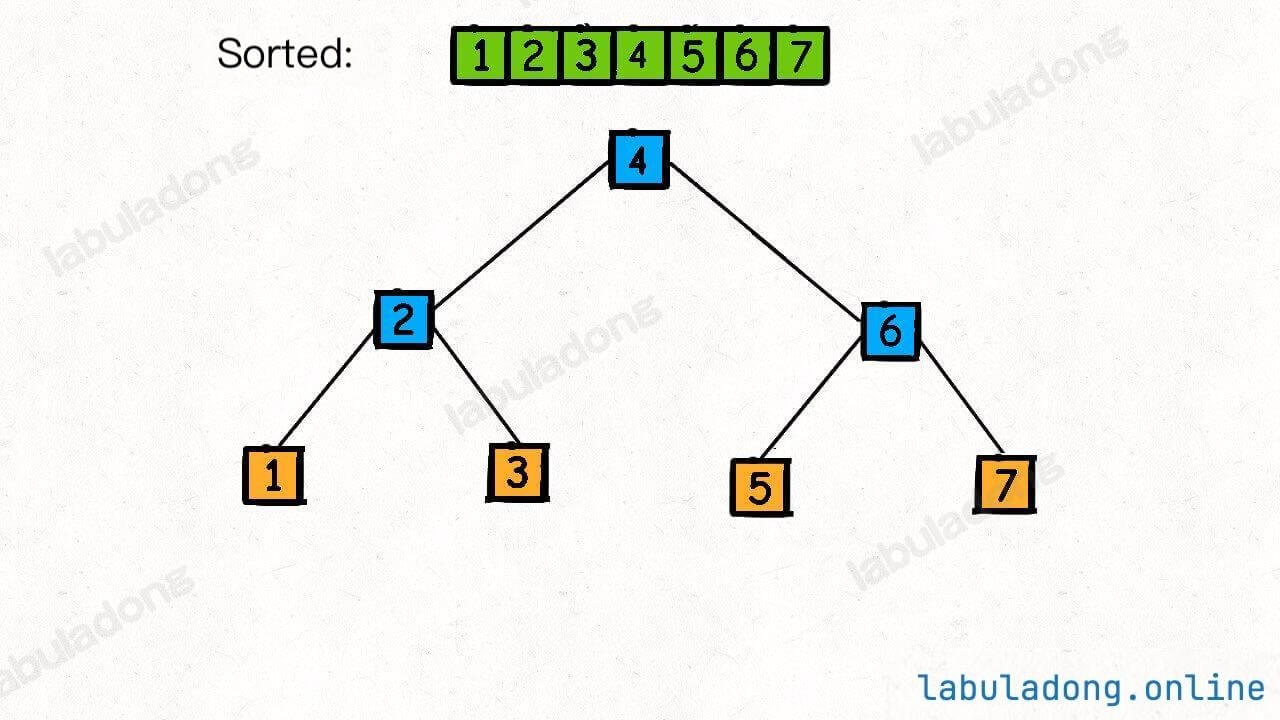
这应该不难理解吧,因为 partition 函数每次都将数组切分成左小右大两部分,恰好和二叉搜索树左小右大的特性吻合。
你甚至可以这样理解:快速排序的过程是一个构造二叉搜索树的过程。
但谈到二叉搜索树的构造,那就不得不说二叉搜索树不平衡的极端情况,极端情况下二叉搜索树会退化成一个链表,导致操作效率大幅降低。
快速排序的过程中也有类似的情况,比如我画的图中每次 partition 函数选出的切分点都能把 nums[lo..hi] 平分成两半,但现实中你不见得运气这么好。
如果你每次运气都特别背,有一边的元素特别少的话,这样会导致二叉树生长不平衡:
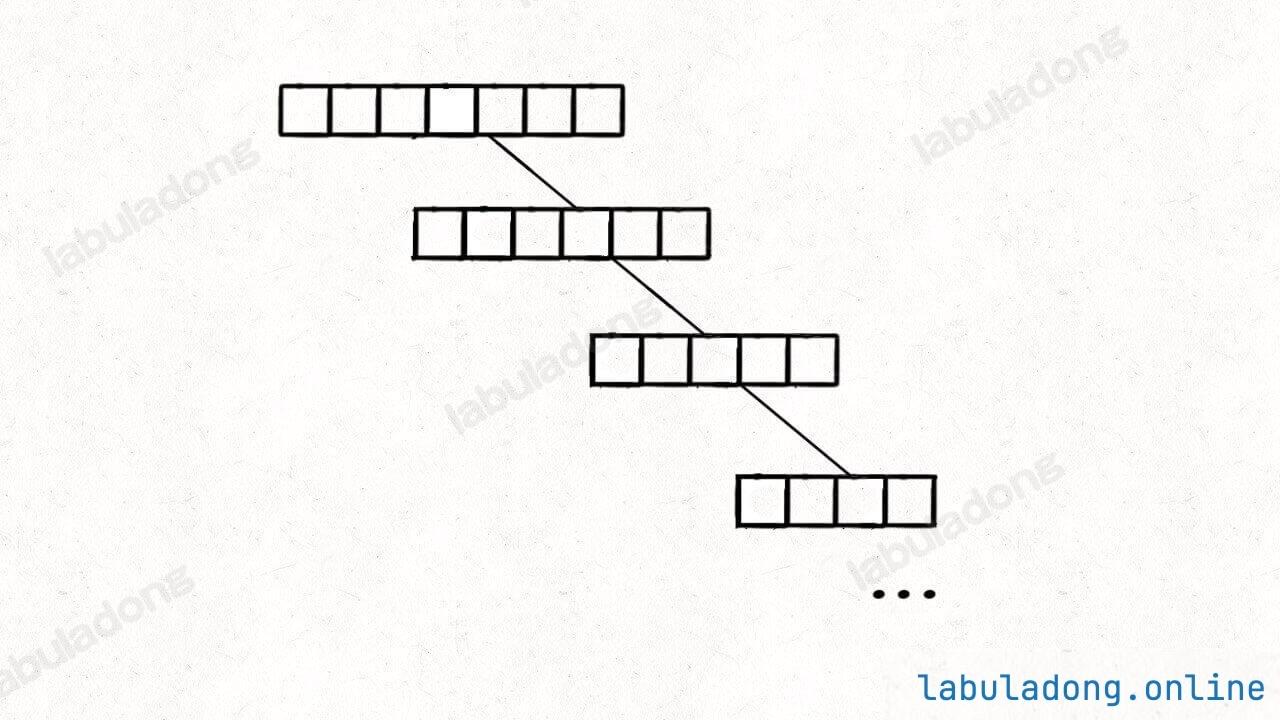
这样的话,时间复杂度会大幅上升,后面分析时间复杂度的时候再细说。
我们为了避免出现这种极端情况,需要引入随机性。
常见的方式是在进行排序之前对整个数组执行 洗牌算法 进行打乱,或者在 partition 函数中随机选择数组元素作为切分点,本文会使用前者。
快速排序代码实现
明白了上述概念,直接看快速排序的代码实现:
import random
class Quick:
@staticmethod
def sort(nums: List[int]):
# 为了避免出现耗时的极端情况,先随机打乱
random.shuffle(nums)
# 排序整个数组(原地修改)
Quick.sort_(nums, 0, len(nums) - 1)
@staticmethod
def sort_(nums: List[int], lo: int, hi: int):
if lo >= hi:
return
# 对 nums[lo..hi] 进行切分
# 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
p = Quick.partition(nums, lo, hi)
Quick.sort_(nums, lo, p - 1)
Quick.sort_(nums, p + 1, hi)
# 对 nums[lo..hi] 进行切分
@staticmethod
def partition(nums: List[int], lo: int, hi: int) -> int:
pivot = nums[lo]
# 关于区间的边界控制需格外小心,稍有不慎就会出错
# 我这里把 i, j 定义为开区间,同时定义:
# [lo, i) <= pivot;(j, hi] > pivot
# 之后都要正确维护这个边界区间的定义
i, j = lo + 1, hi
# 当 i > j 时结束循环,以保证区间 [lo, hi] 都被覆盖
while i <= j:
while i < hi and nums[i] <= pivot:
i += 1
# 此 while 结束时恰好 nums[i] > pivot
while j > lo and nums[j] > pivot:
j -= 1
# 此 while 结束时恰好 nums[j] <= pivot
if i >= j:
break
# 此时 [lo, i) <= pivot && (j, hi] > pivot
# 交换 nums[j] 和 nums[i]
nums[i], nums[j] = nums[j], nums[i]
# 此时 [lo, i] <= pivot && [j, hi] > pivot
# 最后将 pivot 放到合适的位置,即 pivot 左边元素较小,右边元素较大
nums[lo], nums[j] = nums[j], nums[lo]
return j这里啰嗦一下核心函数 partition 的实现,正如前文 二分搜索框架详解 所说,想要正确寻找切分点非常考验你对边界条件的控制,稍有差错就会产生错误的结果。
处理边界细节的一个技巧就是,你要明确每个变量的定义以及区间的开闭情况。具体的细节看代码注释,建议自己动手实践。
贴一个快速排序过程的可视化动画,方便大家理解算法运行的过程:
算法可视化面板
复杂度分析及其他要点
接下来分析一下快速排序的时间复杂度。
显然,快速排序的时间复杂度主要消耗在 partition 函数上,因为这个函数中存在循环。
所以 partition 函数到底执行了多少次?每次执行的时间复杂度是多少?总的时间复杂度是多少?
和归并排序类似,需要结合之前画的这幅图来从整体上分析:
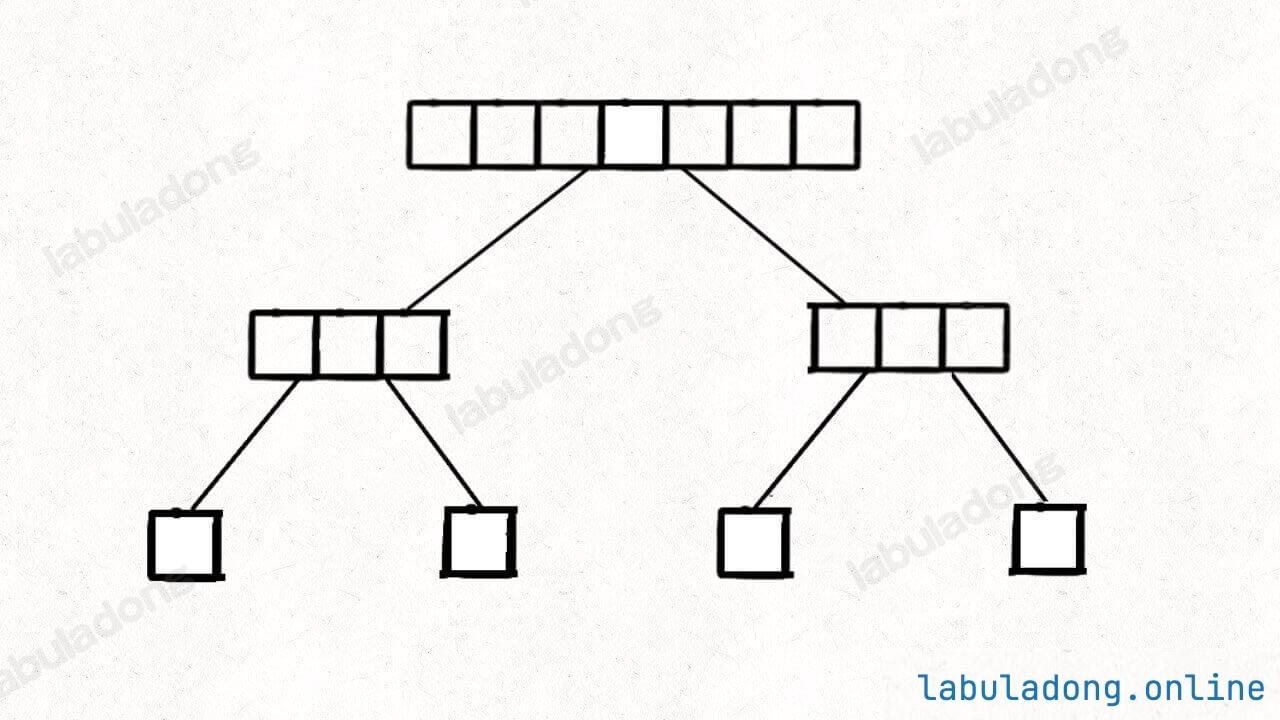
partition 执行的次数是二叉树节点的个数,每次执行的复杂度就是每个节点代表的子数组 nums[lo..hi] 的长度,所以总的时间复杂度就是整棵树中「数组元素」的个数。
假设数组元素个数为 N,那么二叉树每一层的元素个数之和就是 O(N);切分点 p 每次都落在数组正中间的理想情况下,树的层数为 O(logN),所以理想的总时间复杂度为 O(NlogN)。
由于快速排序没有使用任何辅助数组,所以空间复杂度就是递归堆栈的深度,也就是树高 O(logN)。
当然,我们之前说过快速排序的效率存在一定随机性,如果每次 partition 切分的结果都极不均匀:

快速排序就退化成选择排序了,树高为 O(N),每层节点的元素个数从 N 开始递减,总的时间复杂度为:
N + (N - 1) + (N - 2) + ... + 1 = O(N^2)所以我们说,快速排序理想情况的时间复杂度是 O(NlogN),空间复杂度 O(logN),极端情况下的最坏时间复杂度是 O(N2),空间复杂度是 O(N)。
不过大家放心,经过随机化的 partition 函数很难出现极端情况,所以快速排序的效率还是非常高的。
还有一点需要注意的是,快速排序是「不稳定排序」,与之相对的,前文讲的 归并排序 是「稳定排序」。
对于序列中的相同元素,如果排序之后它们的相对位置没有发生改变,则称该排序算法为「稳定排序」,反之则为「不稳定排序」。
如果单单排序 int 数组,那么稳定性没有什么意义。但如果排序一些结构比较复杂的数据,那么稳定排序就有更大的优势了。
比如说你有若干订单数据,已经按照订单号排好序了,现在你想对订单的交易日期再进行排序:
如果用稳定排序算法(比如归并排序),那么这些订单不仅按照交易日期排好了序,而且相同交易日期的订单的订单号依然是有序的。
但如果你用不稳定排序算法(比如快速排序),那么虽然排序结果会按照交易日期排好序,但相同交易日期的订单的订单号会丧失有序性。
在实际工程中我们经常会将一个复杂对象的某一个字段作为排序的 key,所以应该关注编程语言提供的 API 底层使用的到底是什么排序算法,是稳定的还是不稳定的,这很可能影响到代码执行的效率甚至正确性。
说了这么多,快速排序算法应该算是讲明白了,力扣第 912 题「排序数组」就是让你对数组进行排序,我们可以直接套用快速排序的代码模板:
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
# 归并排序对数组进行原地排序
Quick.sort(nums)
return nums
class Quick:
# 见上文快速选择算法
快速排序算法还有一些有趣的变体,比如快速选择算法(Quick Select),主要场景是寻找第 kk 大的元素或者求中位数(k=N/2k=N/2)。
力扣第 215 题「数组中的第 K 个最大元素」就是一道类似的题目,函数签名如下:
def findKthLargest(nums: List[int], k: int) -> int:题目要求我们寻找第 k 个最大的元素,稍微有点绕,意思是去寻找 nums 数组降序排列后排名第 k 的那个元素。
比如输入 nums = [2,1,5,4], k = 2,算法应该返回 4,因为 4 是 nums 中第 2 个最大的元素。
这种问题有两种解法,一种是 二叉堆(优先队列) 的解法,另一种就是快速选择算法,我们分别来看。
二叉堆的解法比较简单,但时间复杂度稍高,直接看代码好了:
import heapq
class Solution:
def findKthLargest(self, nums, k):
# 小顶堆,堆顶是最小元素
pq = []
for e in nums:
# 每个元素都要过一遍二叉堆
heapq.heappush(pq, e)
# 堆中元素多于 k 个时,删除堆顶元素
if len(pq) > k:
heapq.heappop(pq)
# pq 中剩下的是 nums 中 k 个最大元素,
# 堆顶是最小的那个,即第 k 个最大元素
return pq[0]二叉堆(优先队列)是一种能够自动排序的数据结构,我们前文 手把手实现二叉堆数据结构 实现过这种结构,我就默认大家熟悉它的特性了。
核心思路就是把小顶堆 pq 理解成一个筛子,较大的元素会沉淀下去,较小的元素会浮上来;当堆大小超过 k 的时候,我们就删掉堆顶的元素,因为这些元素比较小,而我们想要的是前 k 个最大元素嘛。
当 nums 中的所有元素都过了一遍之后,筛子里面留下的就是最大的 k 个元素,而堆顶元素是堆中最小的元素,也就是「第 k 个最大的元素」。
思路很简单吧,唯一注意的是,Java 的 PriorityQueue 默认实现是小顶堆,有的语言的优先队列可能默认是大顶堆,可能需要做一些调整。
二叉堆插入和删除的时间复杂度和堆中的元素个数有关,在这里我们堆的大小不会超过 k,所以插入和删除元素的复杂度是 O(logk),再套一层 for 循环,假设数组元素总数为 N,总的时间复杂度就是 O(Nlogk)。
这个解法的空间复杂度很显然就是二叉堆的大小,为 O(k)。
快速选择算法是快速排序的变体,效率更高,面试中如果能够写出快速选择算法,肯定是加分项。
首先,题目问「第 k 个最大的元素」,相当于数组升序排序后「排名第 n - k 的元素」,为了方便表述,后文另 k' = n - k。
如何知道「排名第 k' 的元素」呢?其实在快速排序算法 partition 函数执行的过程中就可以略见一二。
我们刚说了,partition 函数会将 nums[p] 排到正确的位置,使得 nums[lo..p-1] < nums[p] < nums[p+1..hi]:
这时候,虽然还没有把整个数组排好序,但我们已经让 nums[p] 左边的元素都比 nums[p] 小了,也就知道 nums[p] 的排名了。
那么我们可以把 p 和 k' 进行比较,如果 p < k' 说明第 k' 大的元素在 nums[p+1..hi] 中,如果 p > k' 说明第 k' 大的元素在 nums[lo..p-1] 中。
进一步,去 nums[p+1..hi] 或者 nums[lo..p-1] 这两个子数组中执行 partition 函数,就可以进一步缩小排在第 k' 的元素的范围,最终找到目标元素。
这样就可以写出解法代码:
import random
class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
# 首先随机打乱数组
random.shuffle(nums)
lo, hi = 0, len(nums) - 1
# 转化成「排名第 k 的元素」
k = len(nums) - k
while lo <= hi:
# 在 nums[lo..hi] 中选一个切分点
p = self.partition(nums, lo, hi)
if p < k:
# 第 k 大的元素在 nums[p+1..hi] 中
lo = p + 1
elif p > k:
# 第 k 大的元素在 nums[lo..p-1] 中
hi = p - 1
else:
# 找到第 k 大元素
return nums[p]
return -1
# 对 nums[lo..hi] 进行切分
def partition(self, nums: List[int], lo: int, hi: int) -> int:
# 见前文
pass这个代码框架其实非常像我们前文 二分搜索框架 的代码,这也是这个算法高效的原因,但是时间复杂度为什么是 O(N) 呢?
显然,这个算法的时间复杂度也主要集中在 partition 函数上,我们需要估算 partition 函数执行了多少次,每次执行的时间复杂度是多少。
最好情况下,每次 partition 函数切分出的 p 都恰好是正中间索引 (lo + hi) / 2(二分),且每次切分之后会到左边或者右边的子数组继续进行切分,那么 partition 函数执行的次数是 logN,每次输入的数组大小缩短一半。
所以总的时间复杂度为:
// 等比数列
N + N/2 + N/4 + N/8 + ... + 1 = 2N = O(N)当然,类似快速排序,快速选择算法中的 partition 函数也可能出现极端情况,最坏情况下 p 一直都是 lo + 1 或者一直都是 hi - 1,这样的话时间复杂度就退化为 O(N2)了:
N + (N - 1) + (N - 2) + ... + 1 = O(N^2)这也是我们在代码中使用 shuffle 函数的原因,通过引入随机性来避免极端情况的出现,让算法的效率保持在比较高的水平。随机化之后的快速选择算法的复杂度可以认为是 O(N)。
到这里,快速排序算法和快速选择算法就讲完了,从二叉树的视角来理解思路应该是不难的,但 partition 函数对细节的把控需要你多花心思去理解和记忆。
最后你可以比较一下快速排序和前文讲的 归并排序 并且可以说说你的理解:为什么快速排序是不稳定排序,而归并排序是稳定排序?



